实验一 感知器及其应用

一：作业信息

博客班级	https://edu.cnblogs.com/campus/ahgc/machinelearning/
作业要求	https://edu.cnblogs.com/campus/ahgc/machinelearning/homework/11950
作业目标	理解感知器算法原理并能针对实际构建感知器模型并进行预测
学号	3180701323

二：实验目的

1. 理解感知器算法原理，能实现感知器算法；
2. 掌握机器学习算法的度量指标；
3. 掌握最小二乘法进行参数估计基本原理；
4. 针对特定应用场景及数据，能构建感知器模型并进行预测。

三：实验内容

1. 安装Pycharm，注册学生版。
2. 安装常见的机器学习库，如Scipy、Numpy、Pandas、Matplotlib，sklearn等。
3. 编程实现感知器算法。
4. 熟悉iris数据集，并能使用感知器算法对该数据集构建模型并应用。

四：实验过程
二分类模型

𝑓(𝑥) = 𝑠𝑖𝑔𝑛(𝑤 ∗ 𝑥 + 𝑏)

损失函数

𝐿(𝑤, 𝑏) = −Σ𝑦𝑖(𝑤 ∗ 𝑥𝑖 + 𝑏)

算法
随机梯度下降法(Stochastic Gradient Descent)
随机抽取一个误分类点使其梯度下降。

𝑤 = 𝑤 + 𝜂𝑦𝑖𝑥𝑖 
𝑏 = 𝑏 + 𝜂𝑦

当实例点被误分类，即位于分离超平面的错误侧，则调整w, b的值，使分离超平面向该无分类点的一侧移动，直至误分类点被正确分类
拿出iris数据集中两个分类的数据和[sepal length，sepal width]作为特征

In [1]:

import pandas as pd
import numpy as np
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
%matplotlib inline

In [2]:

#导入数据
iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)//将特征设置为列
df['label'] = iris.target//增加一列为类别标签

In [3]:

#选择其中的4个特征进行训练
df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']//对四个列进行命名
df.label.value_counts()//确定数据输出频率

In [4]:

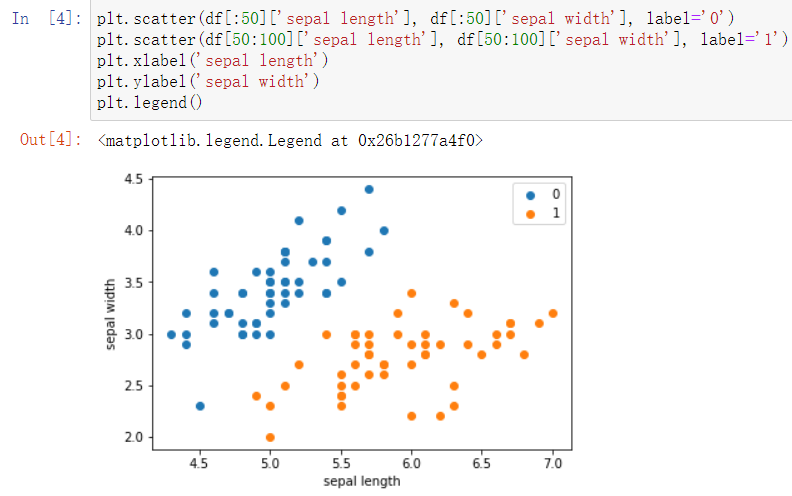
#绘制散点图
plt.scatter(df[:50]['sepal length'], df[:50]['sepal width'], label='0')
plt.scatter(df[50:100]['sepal length'], df[50:100]['sepal width'], label='1')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend()

In [5]:

# 取前100条数据，为了方便展示，取2个特征
data = np.array(df.iloc[:100, [0, 1, -1]])//按行索引,取出第0，1，-1列

In [6]:

X, y = data[:,:-1], data[:,-1]//X为sepal length，sepal width y为标签

In [7]:

y = np.array([1 if i == 1 else -1 for i in y])//将两个类别重新设置为+1 -1

In [8]:

# 数据线性可分，二分类数据
# 此处为一元一次线性方程 
class Model:
    def __init__(self)://将参数w1,w2置为1 b置为0 学习率为0.1
        self.w = np.ones(len(data[0])-1, dtype=np.float32)
        self.b = 0
        self.l_rate = 0.1
        # self.data = data
    def sign(self, x, w, b):
        y = np.dot(x, w) + b
        return y 
    # 随机梯度下降法
    def fit(self, X_train, y_train)://拟合训练数据求w和b
        is_wrong = False
        while not is_wrong:
            wrong_count = 0
            for d in range(len(X_train))://取出样例并进行不断的迭代
                X = X_train[d]
                y = y_train[d]
                if y * self.sign(X, self.w, self.b) <= 0://根据错误的样本点不断的更新和迭代w和b的值
                    self.w = self.w + self.l_rate*np.dot(y, X)
                    self.b = self.b + self.l_rate*y
                    wrong_count += 1
            if wrong_count == 0://当误分类点为0时跳出循环
                is_wrong = True
        return 'Perceptron Model!'
    def score(self):
        pass

In [9]:

#进行拟合
perceptron = Model()
perceptron.fit(X, y)

In [10]:

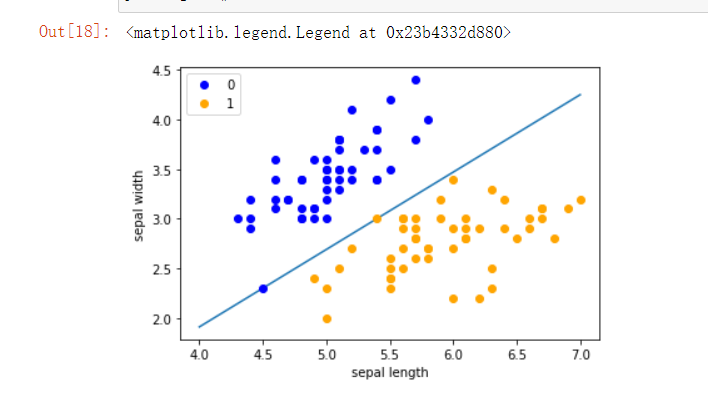
#绘制模型图像
x_points = np.linspace(4, 7,10)
y_ = -(perceptron.w[0]*x_points + perceptron.b)/perceptron.w[1]
plt.plot(x_points, y_)
plt.plot(data[:50, 0], data[:50, 1], 'bo', color='blue', label='0')
plt.plot(data[50:100, 0], data[50:100, 1], 'bo', color='orange', label='1')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend()

In [11]:

#定义感知机
from sklearn.linear_model import Perceptron

In [12]:

#使用训练数据拟合
clf = Perceptron(fit_intercept=False, max_iter=1000, shuffle=False)
clf.fit(X, y)

In [13]:

#输出特征权重矩阵
print(clf.coef_)

In [14]:

#输出截距作为决策函数中常量
print(clf.intercept_)

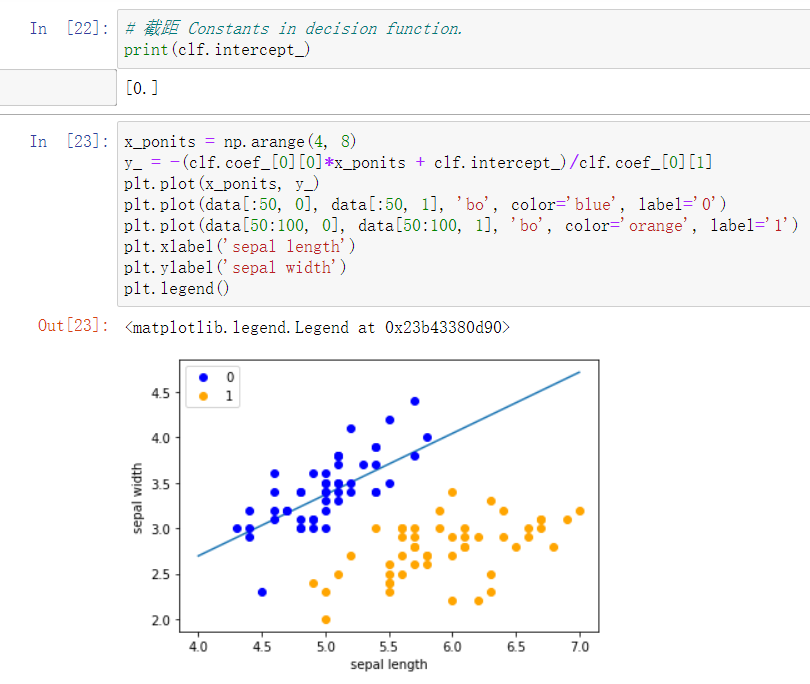
In [15]:

x_ponits = np.arange(4, 8)
y_ = -(clf.coef_[0][0]*x_ponits + clf.intercept_)/clf.coef_[0][1]//确定x轴和y轴的值
plt.plot(x_ponits, y_)//确定拟合的图像的具体信息
plt.plot(data[:50, 0], data[:50, 1], 'bo', color='blue', label='0')
plt.plot(data[50:100, 0], data[50:100, 1], 'bo', color='orange', label='1')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend()

五：实验小结
通过这次实验我对理解感知器算法原理有了更深的理解，能针对一些问题实现感知器算法；也对机器学习算法的度量指标和最小二乘法进行参数估计基本原理有了更好的掌握。