吴恩达机器学习笔记|(7)支持向量机(SVM)
SVM 也被称作大间距分类器。对非线性分类有较好的处理。SVM处理的问题都是凸优化问题,因此找到的几乎都是全局最优值。而神经网络存在局部最优的问题。
一、优化目标
Support vector machine Hypothesis(SVM的数学定义)
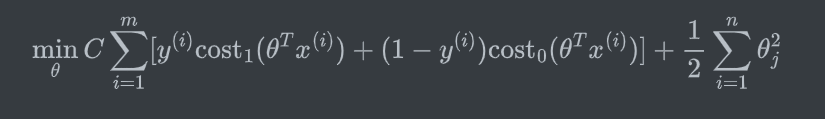
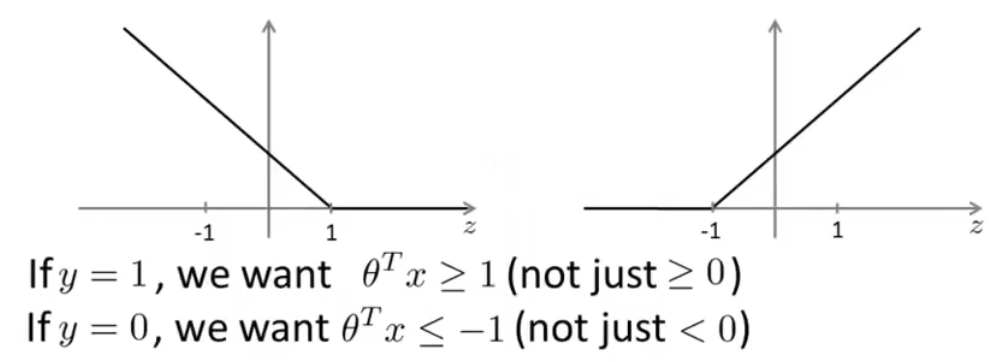
二、SVM的直观解释
假设中的 \(C\) 作用等效于之前逻辑回归中的 \(\frac{1}{\lambda}\) 。若 \(C\) 很大,则假设会对异常点非常敏感(拟合很好甚至过拟合),表现为图中黑色的分界线会变为紫色的分界线;若 \(C\) 很小,则可能会忽略异常点,得到黑线。(\(C\) 的作用类似正则化因子)
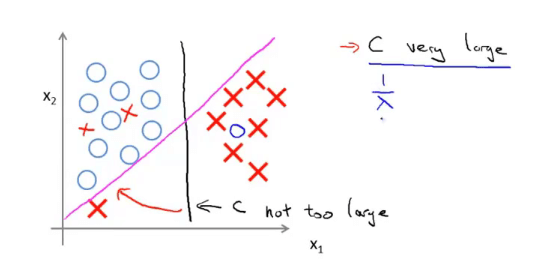
三、SVM的数学原理
-
向量内积(Vector Inner Product)
\(u^Tv=p·||u||=u_1v_1+u_2v_2=v^Tu\)
其中 \(p\) 为向量 \(v\) 在向量 \(u\) 上的投影长度,范数 \(||u||\) 为向量 \(u\) 的长度,\(p,||u||\in\mathbb{R}\),\(u=[u_1,u_2],v=[v_1,v_2]\)。
![Vector Inner Product]()
-
SVM 决策边界
SVM假设为(即 \(C\) 很大,可以不考虑第一项)
![]()
根据向量内积,可将假设转换为
![]()
其中 \(p^{(i)}\) 是 \(x^{(i)}\) 在向量 \(\theta\) 上的投影。假设 \(\theta_0=0\),即向量 \(\theta\) 过原点(该值是否为0对分类效果影响不大)。则分类情况会出现下面几种情况:
![interpretation for SVM'large margin.png]()
由图可见,通过选择右边的决策边界(绿线),可以让两类样本的间隔更远(即投影值 \(p^{(i)}\)),从而使得代价函数值更小。(当 \(p^{(i)}>0\) 且较大时,\(||\theta||\) 很小就能满足约束条件 \(p^{(i)}\cdot\|\theta\|\ge 1\))。即分类器试图最大化训练样本到决策边界的距离——投影值 \(p\)。
四、核函数(Kernel Function)
利用相似度函数(核函数)和标记点来定义**新的特征变量 **\(f\):
\(f_i=\text{similarity}(x,l^{(i)})=\exp(-\frac{||x-l^{(i)}||^2}{2\sigma^2})\)
若 \(x\approx l^{(i)}\):则 \(f_i\approx 1\)
若 \(x\) 离 \(l^{(i)}\) 很远:则 \(f_i\approx 0\)
利用新的特征变量预测y值:
\(\theta_0+\theta_1f_1+\theta_2f_2+\theta_3f_3\ge 3,\quad y=1\)
\(\theta_0+\theta_1f_1+\theta_2f_2+\theta_3f_3< 3,\quad y=0\)
采用核函数的 SVM 运算过程:
-
给定样本集 :\((x^{(1)},y^{(1)},x^{(2)},y^{(2)},\ldots,x^{(m)},y^{(m)})\)
-
选取标记点:
可以直接选择样本点作为标记点。即 \(l^{(1)}=x^{(1)},l^{(2)}=x^{(2)},\ldots,l^{(m)}=x^{(m)}\)
-
计算新的特征变量(映射)
\(f_i=\text{similarity}(x,l^{(i)})\)
\(f=[f_0,f_1,\ldots,f_m],\quad f_0=1\)
映射关系为:
\(x^{(i)}\rightarrow (f_0^{(i)},f_1^{(i)},f_2^{(i)},\ldots,f_m^{(i)})\),即将样本点 \(x^{(i)}\) (可能包含多个特征)映射为特征向量 \(f_i\) 进行后续计算。
-
最终的假设就变为
![]()
SVM参数:
- \(C(=\frac{1}{\lambda})\)
- Large。低偏差,高方差(small λ)
- Small。高偏差,低方差(large λ)
- \(\sigma^2\)
- Large。特征向量 \(f_i\) 非常平滑(变化平缓)。高偏差,低方差
- Small。特征向量 \(f_i\) 非常陡峭(变化剧烈)。低偏差,高方差
使用SVM:
-
选择参数 \(C\)
-
选择核函数
核函数需要满足默塞尔定理。
- 线性核函数——即没有核函数
- 高斯核函数——\(f=\exp(-\frac{||x-l^{(i)}||^2}{2\sigma^2})\),其中 \(x^{(i)}=l^{(i)}\)
- 高斯径向基核函数(Radial Basis Function,RBF)
- 多项式核函数(效果比较差)
- 字符串核函数
- ……
-
多分类
假设有 n 个特征值(\(x\in\mathbb{R}^{n+1}\)),训练样本为 m。
- 若 n 很大,比 m 大(如n=10000,m=10,…1000),则使用逻辑回归或者使用带线性核函数的SVM
- 若 n 很小,m 大小适中(n=1,……,1000,m=10,……10000),则使用带高斯核函数的SVM
- 若 n 很小,m 很大(如n=1,……,1000,m=10000+),尝试找到更多的特征,然后使用逻辑回归或带线性核函数的SVM

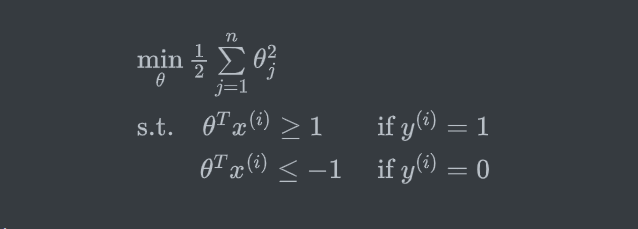

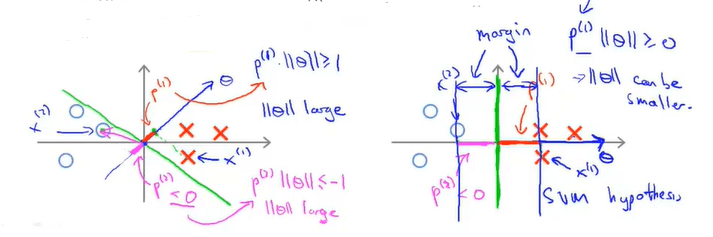


 浙公网安备 33010602011771号
浙公网安备 33010602011771号