吴恩达机器学习笔记|(6)算法选择和算法改进
一、评估假设(欠拟合/过拟合)
-
划分数据集
- 随机划分选取数据(若数据本身已经是随机分布的,则取前70%和后30%即可)
- 训练集 : 测试集 = 7 : 3
-
对线性/逻辑回归评估
-
从训练集学习到参数 \(\theta\)
-
计算测试集误差 \(J_{test}(\theta)\)
-
对于线性回归:
\(J_{\text {test }}(\theta)=\frac{1}{2 m_{\text {test }}} \sum_{i=1}^{m_{\text {test }}}\left(h_{\theta}\left(x_{\text {test. }}^{(i)}\right)-y_{\text {test }}^{(i)}\right)^{2}\)
-
对于逻辑回归:
\(J_{\text {test }}(\theta)=-\frac{1}{m_{\text {test }}} \sum_{i=1}^{m_{\text {test }}} y_{\text {test }}^{(i)} \log h_{\theta}\left(x_{\text {test }}^{(i)}\right)+\left(1-y_{\text {test }}^{(i)}\right) \log h_{\theta}\left(x_{\text {test }}^{(i)}\right)\)
-
或计算错误分类误差(0/1)
![]()
-
-
-
二、模型选择和训练、验证、测试集划分
-
模型选择
- 由于可能存在的过拟合问题,训练集误差不能用于判断新样本的拟合好坏
- 因此需要将数据集划分为training set、validation set、test set,并用 validation set 进行训练误差计算及模型选择,用 test set 进行模型的泛化性能评估
-
训练集、验证集、测试集划分
-
经典比例:6 : 2 : 2
-
用(交叉)验证集而非测试集选择模型
-
Train error
\(J_{\operatorname{train}}(\theta)=\frac{1}{2 m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2}\)
-
Cross Validation error(其实也是计算的训练误差)
\(J_{c v}(\theta)=\frac{1}{2 m_{c v}} \sum_{i=1}^{m_{c v}}\left(h_{\theta}\left(x_{c v}^{(i)}\right)-y_{c v}^{(i)}\right)^{2}\)
-
Test error(测试误差)
\(J_{\text {test }}(\theta)=\frac{1}{2 m_{\text {test }}} \sum_{i=1}^{m_{\text {test }}}\left(h_{\theta}\left(x_{\text {test }}^{(i)}\right)-y_{\text {test }}^{(i)}\right)^{2}\)
-
三、诊断偏差(Bias)与方差(Variance)
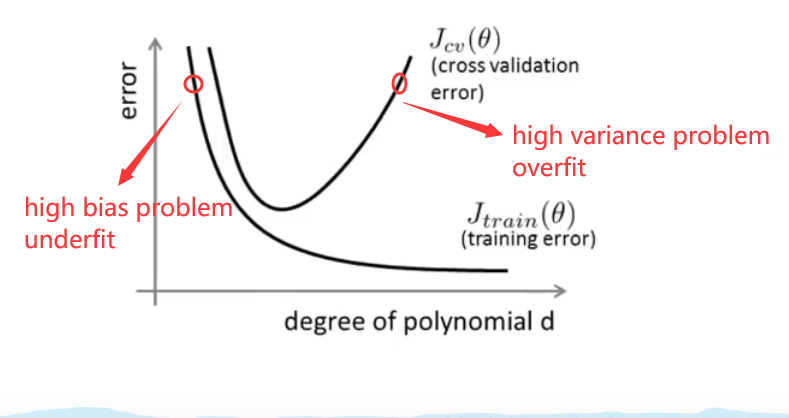
- Bias(underfit)
- \(J_{train}(\theta)\)很大
- \(J_{cv}(\theta)\approx J_{train}(\theta)\)
- Variance(overfit)
- \(J_{train}(\theta)\)很小
- \(J_{cv}(\theta)\gg J_{train}(\theta)\)
四、正则化和偏差/方差
-
执行正则化下各个误差的定义
(不考虑正则化项,即和原来的定义一样,只是训练时求参数加入正则化项)
如:
\(J(\theta)=\frac{1}{2 m_{train}} \sum_{i=1}^{m_{train}}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2}+\frac{1}{2m_{train}}\sum_{j=1}^{m_{train}}\theta_j^2\)
通过以上公式求得\(\theta\),然后再计算误差
\(J_{\operatorname{train}}(\theta)=\frac{1}{2 m_{train}} \sum_{i=1}^{m_{train}}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2}\)
\(J_{c v}(\theta)=\frac{1}{2 m_{c v}} \sum_{i=1}^{m_{c v}}\left(h_{\theta}\left(x_{c v}^{(i)}\right)-y_{c v}^{(i)}\right)^{2}\)
\(J_{\text {test }}(\theta)=\frac{1}{2 m_{\text {test }}} \sum_{i=1}^{m_{\text {test }}}\left(h_{\theta}\left(x_{\text {test }}^{(i)}\right)-y_{\text {test }}^{(i)}\right)^{2}\)
-
自动选择正则化参数 \(\lambda\)
选取一系列\(\lambda\)值,如\(\{\lambda|0,0.01,0.02,0.04,\dots,10\}\),分别利用验证集计算每个模型对应的训练误差进行模型选择,选择最小误差所对应的\(\lambda\)值即可。
-
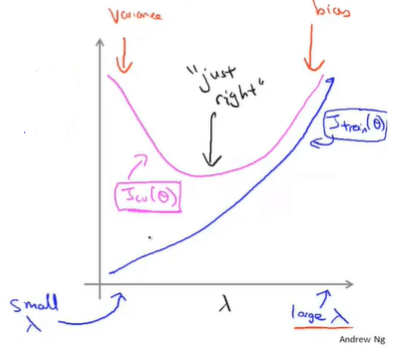
正则化与偏差/方差的关系
- \(\lambda\)较小时,容易出现过拟合问题 —— \(J_{train}\)较小(高方差)
- \(\lambda\)较大时,容易出现欠拟合问题 —— \(J_{train}\)较大(高偏差)
-
考虑underfit和overfit问题的正则化参数\(\lambda\)选择方式
![regularization parameter selection]()
五、学习曲线(Learning Curves)
-
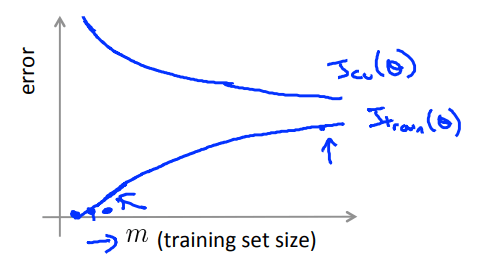
从数据集中选取少量样本,并逐渐增加样本数量m,绘制\(J_{train}\)和\(J_{cv}\)随之变化的曲线
![error varies with the sample number m]()
-
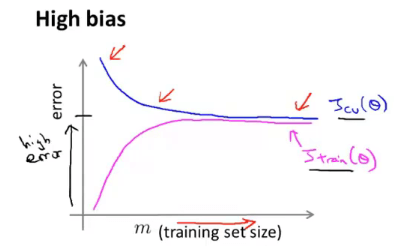
高偏差情况
高偏差情况下,不断增大数据集的样本数量无益。其\(J_{train}\)和\(J_{cv}\)都非常大且值相近,并随着m增大而趋于一个常数。
![J_t&J_cv under high bias]()
-
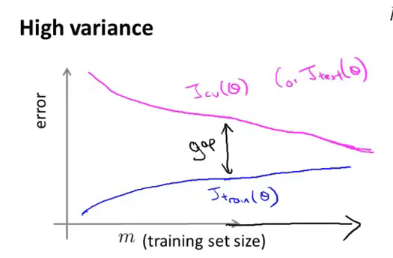
高方差情况
高方差情况下,不断增大数据集样本数量有益。其\(J_{train}\)和\(J_{cv}\)随着样本数m增大而逐渐接近,模型性能逐渐提升。
![J_t&J_cv under high vaiance]()
六、算法改进
-
优化方法
-
更多的训练样本 —— fix high variance
-
更少的特征集合 —— fix high variance
-
更多的额外特征 —— fix high bias
-
增加特征阶数 —— fix high bias
-
减小正则化参数\(\lambda\) —— fix high bias
-
增大正则化参数\(\lambda\) —— fix high variance
-
-
神经网络和过拟合
- 较“小”的神经网络:参数少、更可能欠拟合、计算量小
- 较“大”的神经网络:参数多、更可能过拟合、计算量大
-
误差分析
- 在项目初始尽可能使用简单的算法实现,然后测试
- 使用实际的证据来指导决策
- 数值评价指标。保证可以用数值的方法直观地表现出算法的优劣(如交叉验证)
-
不对称性分类(偏斜类)的误差评估
-
例
癌症分类判断问题。分类算法的误差率是1%,但测试集中患癌症的人可能只有0.5%,相比之下误差率就不能够被接受。
-
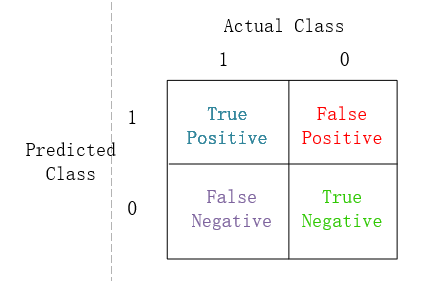
Precision(精确度)/Recall(召回率)
Precision=真阳性/(真阳性+假阳性)
Recall=真阳性/(真阳性+假阴性)
![Precision&Recall]()
-
拥有高Precision和高Recall的模型表现很好
-
精确度和召回率的权衡
-
通过调节判决条件可对最后结果的精确度和召回率进行调整
-
如希望非常确信是癌症才告诉病人,则可调高判决条件,此时模型拥有较高的精确度和较低的召回率。
-
若我们不想放过任何一个可能错判的情况,则可调低判决条件,此时模型拥有较低的精确度和较高的召回率。
-
-
也可画出精确度和召回率的曲线,取二者均较高的临界值
-
通过 \(F_1\) Score 来获取较好的精确度和召回率
- \(F_1 = 2\frac{PR}{P+R}\)
- 要获得较好的 \(F_1\),\(P\) 和 \(R\) 都要接近于1
-
-
七、机器学习数据
- 要确定能够根据特征获得想要的输出
- 确定能够采集到一个拥有多个特征的庞大数据集

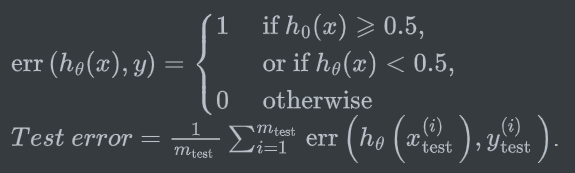

 浙公网安备 33010602011771号
浙公网安备 33010602011771号