吴恩达机器学习笔记|(5)神经网络(Neural-Network)
一、非线性假设
当输入特征数量非常大时,线性假设不再适用。
二、神经元与大脑
“神经重接实验”: 让处理听觉的神经断开,转而接上视觉神经的信息输入,听觉神经会学会“看到”东西。也许存在一种学习算法,可以同时实现对视觉、听觉、触觉等的处理,让大脑自己学习如何处理不同的数,而不用大量不同的算法分开处理。
三、模型
-
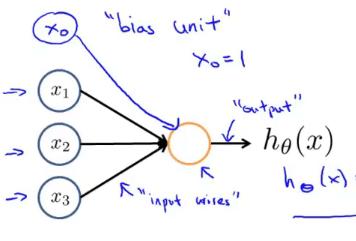
Neuron Model: Logistic Unit
![Neuron Model]()
-
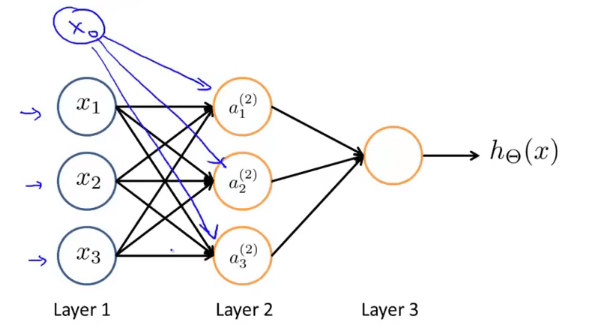
Neural Network
![Neural Network]()
-
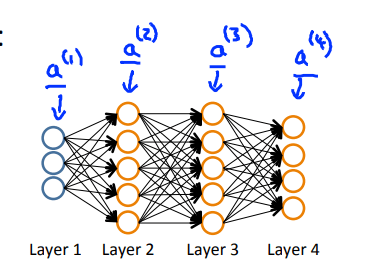
输入层(Input Layer) + 隐藏层(Hidden Layer) + 输出层(Output Layer)
-
\(a_i^{(j)}\): 第\(j\)层的第\(i\)个单元的“activation”,即激活项,指由一个具体神经元计算并输出的值
-
\(\theta^{(j)}\): 权重矩阵。控制从第\(j\)层到第\(j+1\)层的映射
-
\(x_0或a_0^{(2)}\): 偏置单元(bias unit)
-
g: 指sigmoid函数
![computation process]()
-
-
计算过程
-
前向传播(Forward Propagation): 从输入层到隐藏层到输出层,计算每一层激活项的值。可以求出代价函数值。
-
后向传播(Back Propagation): 从输出层到隐藏层到输入层,累加计算代价函数的偏导数。回传误差,得到梯度,更新权重。
-
特征
与逻辑回归相似,只是用于训练的特征并非\(x_1,x_2,...,x_n\),而是隐藏层计算出来的\(a_i^{(j)}\)
-
-
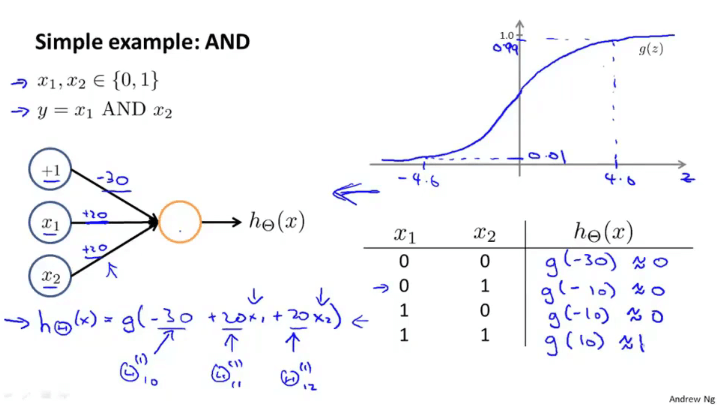
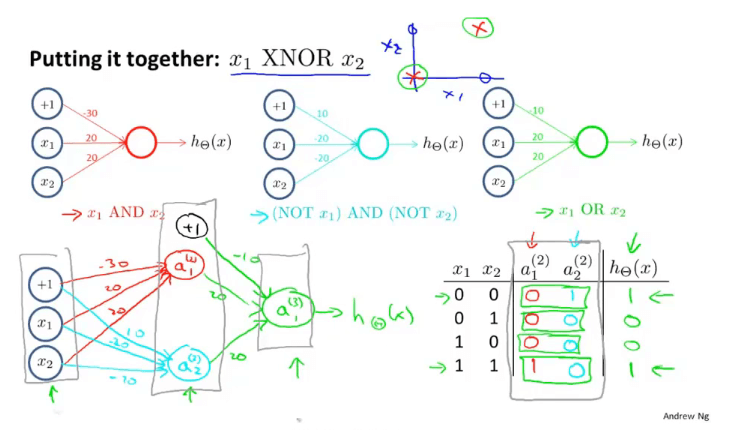
实例(非线性函数计算的实现与理解)
- 使用不断深入的神经网络层可以计算更加复杂的函数
- 每一层隐藏层用于计算更加复杂的特征,这些特征被用于逻辑回归分类器的最后一层(输出层)
-
多元分类问题
-
手写数字识别
-
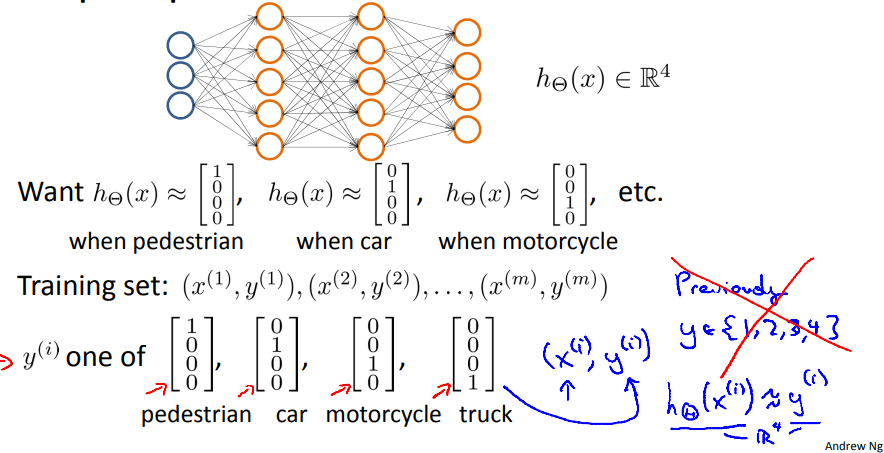
多目标识别
![多目标识别]()
![多目标识别-网络结构]()
-
四、代价函数
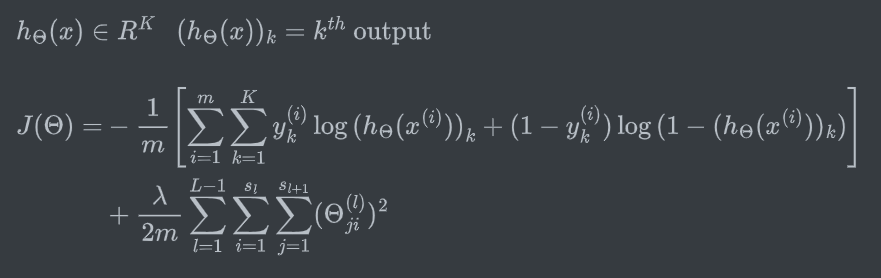
- \(L\): 网络总层数
- \(s_L\): 每层的单元数
- \(K\): 输出单元数。也即需要分类的数量(如识别车、人、人行道,则K=3)
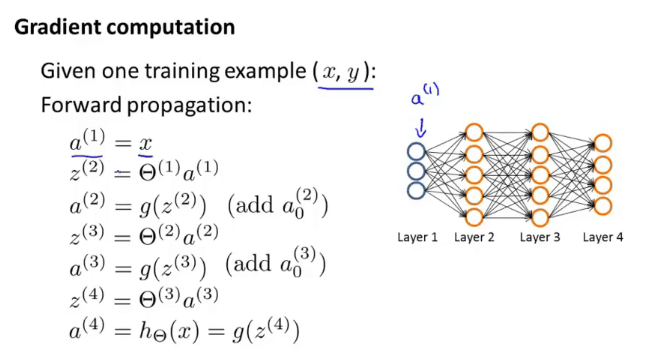
五、前向传播算法(Forward Propagation)
-
功能:逐层求激活项并求出代价函数
-
计算过程
![Forward Propagation]()
六、后向传播算法(Back Propagation)
功能:计算每一层代价函数的偏导数\(\frac{\partial}{\partial\Theta_{ij}^{(l)}}J(\Theta)\),最小化代价函数(因为需要利用梯度下降法求参数)
网络结构:
-
\(\min_\limits{\Theta}J(\Theta)\)
需要计算:\(J(\Theta)\),\(\frac{\partial}{\partial\Theta_{ij}^{(l)}}J(\Theta)\)
-
前置说明:
-
\(sigmoid\)函数的性质: \(g(x)'=g(x)(1-g(x))\)
-
中间变量\(z\): \(z^{(l)}=(\Theta^{(l-1)})a^{(l-1)}\)
-
第\(l\)层神经元的误差: \(\delta^{(l)}=\frac{\partial J(\theta)}{\partial z^{(l)}}\)(向量。第\(l\)层第\(j\)个神经元的误差\(\delta_j^{(l)}\),\(J(\theta)\)是每一层的代价函数)
误差公式理解:每一层中间值\(z^{(l)}\)的变化会影响到神经网络输出值\(h_\theta(x)\),进而影响到代价函数\(J(\theta)\)。
因此\(\frac{\partial J(\theta)}{\partial z^{(l)}}\)表示神经元加权输入\(z^{(l)}\)的变化给代价函数\(J(\theta)\)带来的变化梯度。
-
-
应用链式求导法则求出每一层的误差
-
layer 4的误差:\(\delta^{(4)}=a^{(4)}-y\)(都是向量)
-
layer 3的误差:\(\delta^{(3)}=(\Theta^{(3)})^T\delta^{(4)}.*g'(z^{(3)})\)(各向量具体顺序取决于数据的实际维度)
-
链式求导
![]()
求导说明:将代价函数简化表示为:
\(J(\theta)=-y \log h(x)-(1-y) \log (1-h(x))=-y \log a^{(4)}-\) \((1-y) \log \left(1-a^{(4)}\right)\)
所以:
- \(\frac{\partial J}{\partial a^{(4)}}=\left(\frac{-y}{a^{(4)}}+\frac{1-y}{1-a^{(4)}}\right)\)
Sigmoid函数的导数为: \(g^{\prime}(z)=g(z)(1-g(z))\) , 所以:
- \(\frac{\partial a^{(4)}}{\partial z^{(4)}}=\frac{\partial g\left(z^{(4)}\right)}{\partial z^{(4)}}=a^{(4)}\left(1-a^{(4)}\right)\)
-
-
layer 2的误差:\(\delta^{(2)}=(\Theta^{(2)})^T\delta^{(3)}.*g'(z^{(2)})\)
-
-
BP算法流程
![Back Propagation]()
- \(D_{ij}^{(l)}\)表示第\(i\)个样本,在第\(l\)层的第\(j\)个节点的代价函数的梯度,可以利用该梯度对权重矩阵\(\Theta\)执行梯度下降或者另外一个高级优化算法。
- 注意\(\Delta_{ij}^{(l)}=\Delta_{ij}^{(l)}+a_j^{(l)}\delta_i^{(l+1)}\)是根据 \(\delta^{(l)}=\frac{\partial J(\theta)}{\partial z^{(l)}}\)推导得出。\(z^{(l)}=(\Theta^{(l-1)})a^{(l-1)}\)
七、梯度检测
梯度的数值估计。用来检验BP算法的正确性。注意在检验完二者得出的梯度值相近(仅在小数有差异)后进行数据训练前,需要禁止梯度数值的代码(因为很慢)。
-
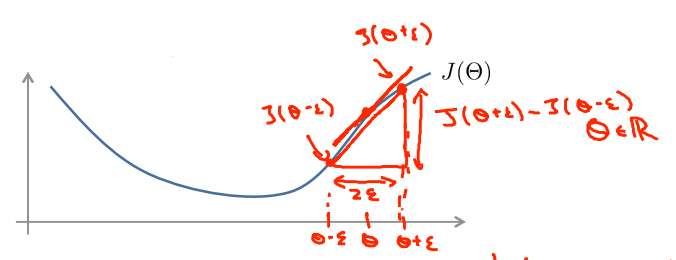
梯度的数值估计(\(\theta\)为标量时)
![Numerical estimation of gradients]()
-
双侧差分法(更准确)
\(\frac{\partial J(\theta)}{\partial\theta}\approx \frac{J(\theta+\varepsilon)-J(\theta-\varepsilon)}{2\varepsilon}\)(\(\varepsilon=10^{-4}\))
-
单侧差分法
\(\frac{\partial J(\theta)}{\partial\theta}\approx \frac{J(\theta+\varepsilon)-J(\theta)}{\varepsilon}\)
-
-
梯度的数值估计(\(\theta\)为矢量时)
![Numerical estimation of gradients]()
八、随机初始化
初始化时\(\Theta\)值不能为0,这会导致每一层的隐藏神经元得到的值相同,而无法计算复杂函数,提取不了特征。(对称权重问题)
-
一般将每个\(\Theta_{ij}^{(l)}\)初始化为\([-\varepsilon,\varepsilon]\)之间的一个值
theta=rand(10,11)*(2*INIT_EPSILON)-INIT_EPSILON;(rand(10,11): 10*11的矩阵,元素值在(0,1)间)
九、训练神经网络
-
随机初始化权重\(\Theta_{ij}^{(l)}\),通常很小,接近零但不等于零
-
通过前向传播算法得到每个输入值\(x^{(i)}\)的输出项\(h_{\Theta}(x^{(i)})\)
-
计算出代价函数\(J(\Theta)\)
-
通过后向传播算法求\(J(\Theta)\)的偏导\(\frac{J(\Theta)}{\partial\Theta_{jk}^{(l)}}\)
-
梯度检验。用BP算法得到的偏导和数值估计法所得进行比较验证。然后注释梯度检验的代码。
-
使用梯度下降或高级优化方法计算令\(J(\Theta)\)最小化的参数 \(\Theta\)

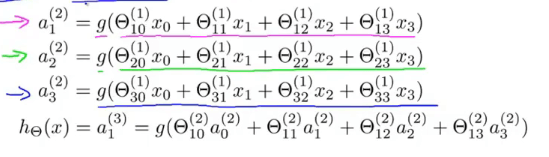






 浙公网安备 33010602011771号
浙公网安备 33010602011771号