吴恩达机器学习笔记|(4)过拟合问题及正则化(Overfitting®ularization)
一、欠/过拟合问题(Under fitting/Overfitting Problem)
-
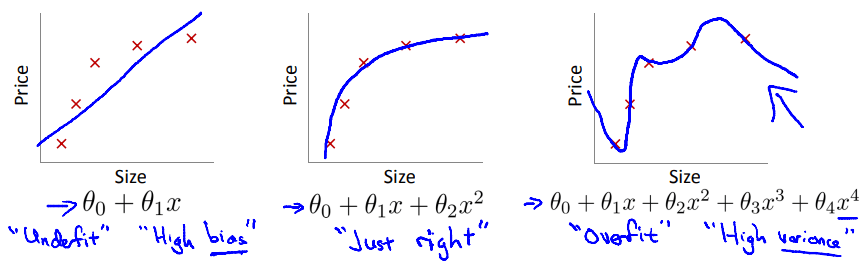
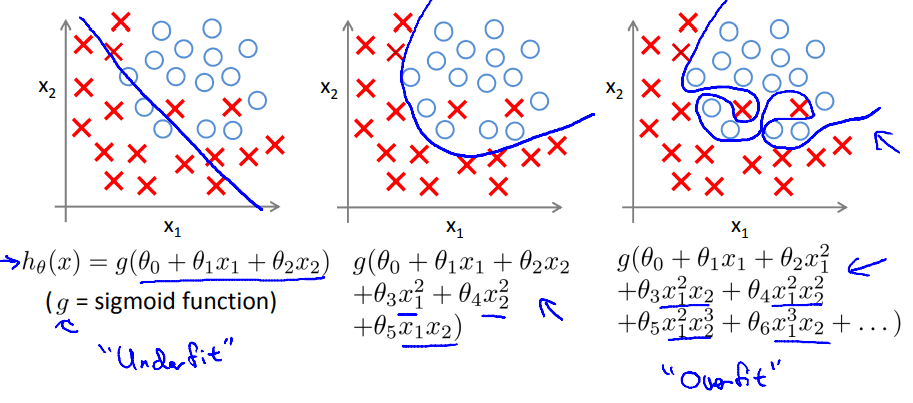
欠拟合
拟合偏差非常大,用于预测时误差也会非常大。
-
过拟合
方差非常大,即拟合曲线与训练数据拟合得非常好以至于曲线非常复杂,导致缺乏足够的数据来约束,不能很好地泛化到新的样本数据中。
-
解决拟合问题
- 减少特征的数量
- 人工选择
- 自动选择算法
- 正则化(Regularization)
- 保留所有的特征,但减少参数的数量级
- 减少特征的数量
二、正则化(Regularization)
-
在优化目标函数中加入惩罚项以缩小参数值(\(\lambda\)为正则化参数)
\(\min_\limits{\theta}[\frac{1}{2m}\sum_\limits{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2+{\color{red}\lambda\sum_\limits{j=1}^n\theta_j^2}]\)(一般不会用\(\theta_0\),但影响不大)
-
更小的参数值意味着更简单的假设函数和更平滑的拟合曲线。
-
但是正则化参数 \(\lambda\) 不能太大,否则相当于只含\(\theta_0\),会导致欠拟合
-
-
例:
如一个有3个参数的目标函数,在其后加入\(\lambda(\theta_3+\theta_4)\)项,且\(\lambda\)很大,则要使整个目标函数最小,必然要让\(\theta_3,\theta_4\)接近0,相当于忽略了这两个参数。
\(\min_\limits{\theta}[\frac{1}{2m}\sum_\limits{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2+{\color{red}\lambda(\theta_3^2+\theta_4^2)}]\)
三、正则化线性回归
-
梯度下降法
-
目标函数
\(\min_\limits{\theta}\frac{1}{2m}[\sum_\limits{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2+{\lambda\sum_\limits{j=1}^n\theta_j^2}]\)
-
迭代过程
![]()
其实就是每次迭代的时候都将 \(\theta_j\) 缩小一点
-
-
正规方程
正则化还能解决样本数量小于特征数量时矩阵不可逆的问题。加入 \(\lambda\) 矩阵项后,括号内的矩阵一定可逆
![Normal Func]()
四、正则化逻辑回归
-
目标函数
\(\min_\limits{\theta}-\frac{1}{m}\left[\sum_\limits{i=1}^my^{(i)}\log(h_\theta(x^{(i)}))+(1-y^{(i)})\log(1-h_\theta(x^{(i)}))\right]+\frac{\lambda}{2m}\sum_\limits{j=1}^n\theta_j\)
-
迭代过程
![]()
五、高级优化算法的正则化应用


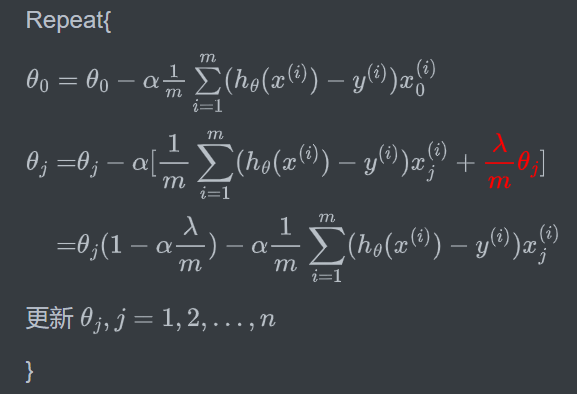

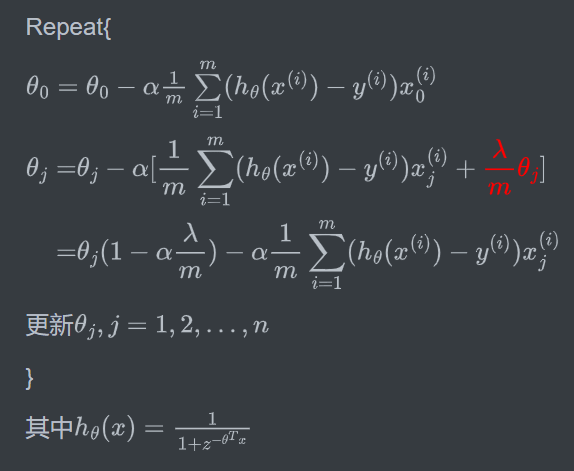

 浙公网安备 33010602011771号
浙公网安备 33010602011771号