吴恩达机器学习笔记|(3)逻辑回归(Logistic-Regression)
一、分类问题介绍
\(y\in\{0,1\}\)
- 0: Negative Class
- 1: Positive Class
例子:邮件分类;肿瘤分类;
Logistic Regression的特点
- 其预测值介于0-1间,而不会大于1或小于0
- 事实上并不是回归,而是分类,命名属于历史问题
二、Logistic Regression Model
-
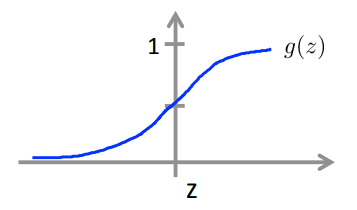
假设函数: \(h_\theta(x)=g(\theta^Tx)\)
-
\(g(z)=\frac{1}{1+e^{-z}}\)
![g(z)]()
-
其输出为 \(h_\theta(x)=P(y=1|x;\theta)或P(y=0|x;\theta)\)
- \(predict\ {}''y=1''\ if\ h_\theta(x)\ge0.5\)
- \(predict\ {}''y=0''\ if\ h_\theta(x)<0.5\)
-
-
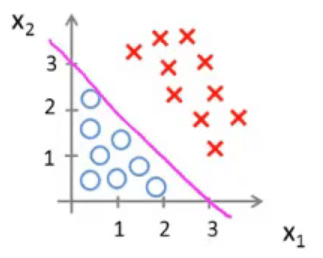
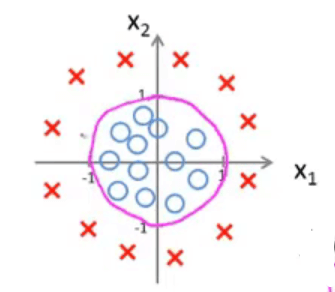
决策边界
是假设和参数本身的属性,而非由数据集定义。数据集用于拟合参数
![Decision Boundary-1]()
![Decision Boundary-2]()
-
代价函数(优化目标)
因为直接代入sigmoid函数时,代价函数并不是凸函数,使用梯度下降法很难得到全局最优值。因此用log操作将其转化为凸函数。
-
代价函数: \(J(\theta)=\frac{1}{m}\sum_\limits{i=1}^m\mathrm{Cost}(h_\theta(x^{(i)},y^{(i)})\)
-
单样本代价函数:
![]()
![Cost Func]()
-
代价函数简化: \(J(\theta)=-\frac{1}{m}\left[\sum_\limits{i=1}^my^{(i)}\log(h_\theta(x^{(i)}))+(1-y^{(i)})\log(1-h_\theta(x^{(i)}))\right]\)
-
拟合得到参数\(\theta\): \(\min_\limits{\theta}{J(\theta)}\)
Repeat {
\(\theta_j=\theta_j-\alpha\frac{1}{m}\sum_\limits{i=1}^m(h_\theta(x^{(i)})-y^{(i)})x^{(i)}_j\)
} -
预测分类结果: \(h_\theta(x)=g(\theta^Tx)\)
-
三、高级优化
优点:不需要选择学习速率 \(\alpha\) ,比梯度下降收敛更快
缺点:更加复杂
在MATLAB/Octave中有内置函数实现
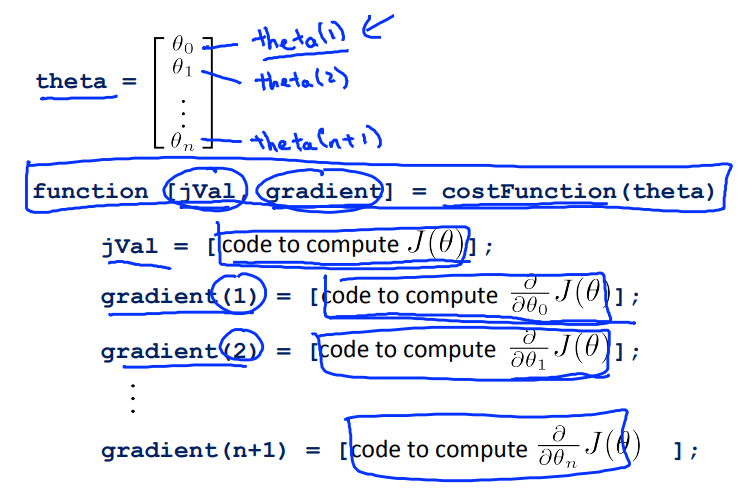
- 共轭梯度(Conjugate gradient)
- BFGS
- L-BFGS
四、多类别分类(Multiclass Classification)
-
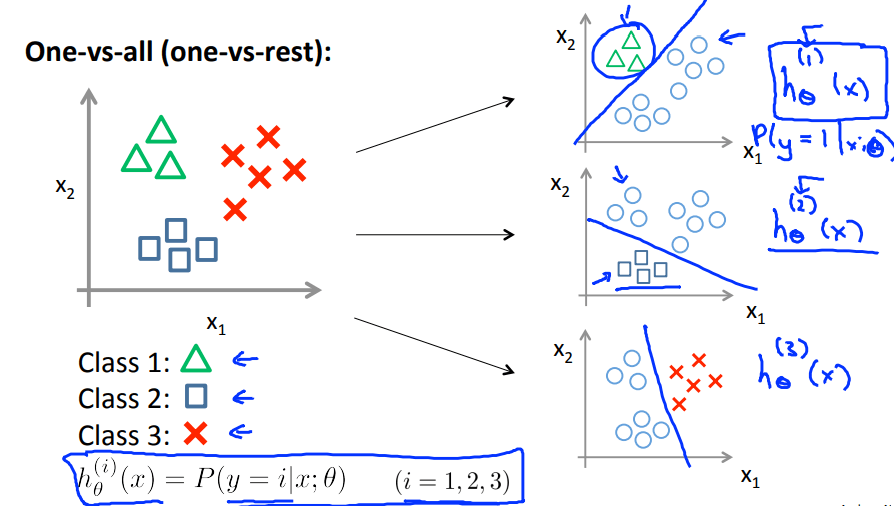
应用Logistic Regression的思路
训练对应类别个分类器,再进行测试,将输入分别代入三个分类器,取最大输出值为最终预测值。
![Multiclass Classification]()


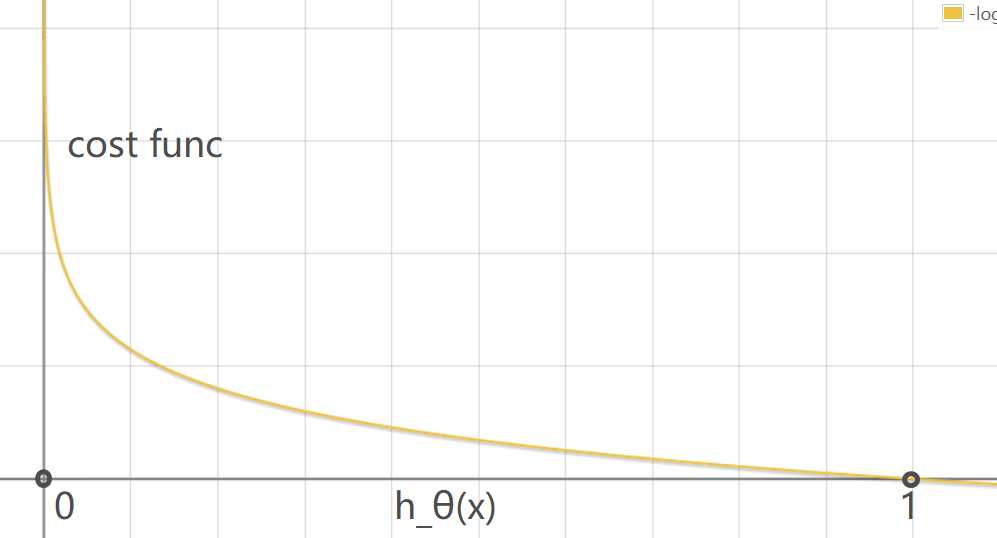

 浙公网安备 33010602011771号
浙公网安备 33010602011771号