最优性条件

非线性规划的最优解所满足的必要条件和充分条件（仅包含定理）

注意：文中很多地方的变量其实是矢量，比如方向 $d$ 和梯度，为了方便写都没有写粗体。

一、无约束问题的最优性条件

• 定理 7.1.1 （其它定理证明需要的基础定理）

  设函数 $f(x)$ 在点 $\bar{x}$ 处可微，如果存在方向 ${d}$ ，使得 $\nabla f(\bar{{x}})^{\mathrm{T}} {d}<0$ ，则存在 $\delta>0$ ，使得对每个 $\lambda\in(0,\delta)$，有 $f(\bar{x}+\lambda d)<f(\bar{x})$.

• 定理 7.1.2 （局部极小点的一阶必要条件）

  设函数 $f(x)$ 在点 $\bar{x}$ 处二次可微，若点 $\bar{x}$ 是局部极小点，则梯度 $\nabla f(\bar{x})={0}$.

• 定理 7.1.3 （局部极小点的二阶必要条件）

  设函数 $f(x)$ 在点 $\bar{x}$ 处二次可微，若点 $\bar{x}$ 是局部极小点，则梯度 $\nabla f(\bar{x})=\boldsymbol{0}$，且 Hesse 矩阵 $\nabla^{2} f(\bar{x})$ 半正定.

• 定理 7.1.4 局部极小点的二阶充分条件

  设函数 $f(x)$ 在点 $\bar{x}$ 处二次可微，若梯度 $\nabla f(\bar{x})={0}$，且 Hesse 矩阵 $\nabla^{2} f(\bar{x})$ 正定，则 $\bar{x}$ 是局部极小点.

• 定理 7.1.5 （函数凸性假设下，全局极小点的充要条件）

  设函数 $f(x)$ 是定义在 $\mathbb{R}^n$ 上的可微凸函数，$\bar{x}\in\mathbb{R^n}$ ，则 $\bar{x}$ 是全局极小点的充分必要条件是梯度 $\nabla f(\bar{x})={0}$.

二、含约束问题的最优性条件

2.1 含约束的极值问题表示

有约束的极值问题

$$\begin{array}{ll} \min & f(\boldsymbol{x}) \quad {x} \in \mathbb{R}^{n} \\ \text { s.t. } & g_{i}({x}) \geqslant 0, \quad i=1, \cdots, m, \\ & h_{j}({x})=0, \quad j=1, \cdots, l, \end{array}$$

其中，$g_{i}({x}) \geqslant 0$ 为不等式约束，$h_{j}({x})=0$ 为等式约束，集合

$$S=\left\{{x} \mid g_{i}({x}) \geqslant 0, i=1, \cdots, m ; h_{j}({x})=0, j=1, \cdots, l\right\}$$

称为可行域。

2.2 可行方向与下降方向

• 下降方向

  设函数 $f(x)$ 是定义在 $\mathbb{R}^n$ 上的实函数，$\bar{x}\in\mathbb{R^n}$ ，$d$ 是非零向量，若存在数 $\delta>0$ ，使得对每个 $\lambda\in(0,\delta)$​，都有

  $$f(\bar{x}+\lambda d)<f(\bar{x})$$

  则称 $d$ 是函数 $f(x)$ 在 $\bar{x}$ 处的下降方向。

  如果 $f(x)$ 是可微函数，且 $\nabla f(\bar{{x}})^{\mathrm{T}} {d}<0$ ，则根据定理 7.1.1，$d$ 是函数 $f(x)$ 在 $\bar{x}$ 处的下降方向，记作

  $$F_{0}=\left\{{d} \mid {\nabla} f(\overline{{x}})^{\mathrm{T}} {d}<0\right\}$$

• 可行方向

  设集合 $S \subset \mathbb{R}^{n},\bar{x}\in \mathrm{cl}\;S$，$d$ 是非零向量，若存在数 $\delta>0$ ，使得对每个 $\lambda\in(0,\delta)$，都有

  $$\bar{x}+\lambda d \in S$$

  则称 $d$ 是集合 $S$ 在 $\bar{x}$ 处的可行方向。其中 "cl" 表示闭包。

  集合 $S$ 在在 $\bar{x}$ 处的可行方向组成的集合

  $$D=\{{d} \mid {d} \neq \mathbf{0}, \overline{{x}} \in \mathrm{cl}\; S, \exists \delta>0 \text {, 使得 } \forall \lambda \in(0, \delta) \text {, 有 } \overline{{x}}+\lambda {d} \in S\}$$

  称为在 $\bar{x}$ 处的可行方向锥。

• 定理 7.2.1

  设 $S$ 是 $\mathbb{R}^{n}$ 中的非空集合，$\bar{x}\in S$， $f(x)$ 在点 $\bar{x}$ 处可微，若 $\bar{x}$ 是局部最优解，则 $F_{0} \cap D=\varnothing$. 即若 $\bar{x}$ 是局部最优解，则 $\bar{x}$ 处的可行方向一定不是下降方向。

2.3 不等式约束问题

非线性规划问题

$$\begin{array}{ll} \min & f({x}) \\ \text { s. t. } & g_{i}({x}) \geqslant 0, \quad i=1, \cdots, m . \end{array}$$

可行域为

$$S=\left\{{x} \mid g_{i}({x}) \geqslant 0, i=1, \cdots, m\right\}$$

其约束条件在点 $\bar{x}\in S$ 有两种情形：

• 在点 $\bar{x}$ 处起作用约束（下标集用 $I$ 表示）

  $$g_{i}(\bar{x})=0, \quad i \in I$$

• 在点 $\bar{x}$ 处不起作用约束

  $$g_{i}(\bar{x})>0, \quad i \notin I .$$

  • 用 $I$ 表示起作用约束下标集

    $$I=\left\{i \mid g_{i}(\bar{{x}})=0\right\}$$

  • 用 $G_0$ 替代定理 7.2.1 中的可行方向锥 $D$

    $$G_{0}=\left\{{d} \mid \nabla{g_{i}}(\bar{{x}})^{\mathrm{T}} {d}>0, i \in I\right\}$$

• 定理 7.2.2（由7.2.1变化而来）—— 最优性的几何表示

  设 $\bar{x}\in S$， $f(x)$ 在点 $\bar{x}$ 处可微，$g_i(x)(i\notin I)$ 在 $\bar{x}$ 连续，若 $\bar{x}$ 是局部最优解，则

  $$F_{0} \cap G_0=\varnothing$$

• 定理 7.2.3 （Fritz John条件）—— 最优性的代数表示

  设 $\bar{x}\in S$，$I=\{i|g_i(\bar{x})=0\}$， $f,g_i\in I$ 在点 $\bar{x}$ 处可微，$g_i(x)(i\notin I)$ 在 $\bar{x}$ 连续，若 $\bar{x}$ 是局部最优解，则存在不全为0的非负数 $w_0,w_i(i\in I)$ ，使得

  $$w_{0} \nabla f(\bar{x})-\sum_{i \in I} w_{i} \nabla g_{i}(\bar{x})=0$$

  证明需要用到 Gordan 定理，即 如果一组基的非负组合是一个凸锥，则等价为这组基的正组合表示不了原点，除非系数都是0（两个条件只有一个成立）

• 定理 7.2.4 （Kuhn-Tucker 条件）—— K-T条件，在Fritz John条件基础上增加了起约束作用的梯度线性无关的约束规格（对约束条件的限制），以避免出现 $w_0=0$ 的情形。

  设 $\bar{x}\in S$​，$I=\{i|g_i(\bar{x})=0\}$​， $f,g_i\in I$​ 在点 $\bar{x}$​ 处可微，$g_i(x)(i\notin I)$​ 在 $\bar{x}$​ 连续，$\left\{\nabla g_{i}(\bar{x}) \mid i \in I\right\}$​ 线性无关， 若 $\bar{x}$​ 是局部最优解，则存在非负数 $w_i(i\in I)$​ ，使得

  $$\nabla f(\bar{{x}})-\sum_{i \in I} w_{i} \nabla g_{i}(\bar{{x}})=\mathbf{0}$$

  若 $g_i(x)(i\notin I)$ 在点 $\bar{x}$ 处可微，K-T 条件可等价表示为

  $$\begin{aligned} &\nabla f(\bar{x})-\sum_{i=1}^{m} w_{i} \nabla g_{i}(\bar{{x}})=\mathbf{0}, \\ &w_{i} g_{i}(\bar{x})=0, \quad i=1, \cdots, m, \\ &w_{i} \geqslant 0, \quad i=1, \cdots, m . \end{aligned}$$

  其中，$w_{i} g_{i}(\bar{x})=0$ 称为互补松弛条件。

• 定理 7.2.5 凸优化问题最优解的一阶充分条件

  设问题中 $f$ 是凸函数，$g_i(i=1,2,\cdots,m)$ 是凹函数（注意不等式约束 $g_i$ 的符号（若是 $g_i\le0$ ，则应该是凸函数），$S$ 是可行域，$\bar{x}\in S$，$I=\{i|g_i(\bar{x})=0\}$， $f,g_i\in I$ 在点 $\bar{x}$ 处可微，$g_i(x)(i\notin I)$ 在 $\bar{x}$ 连续，K-T 条件成立，则 $\bar{x}$ 为全局最优解。

2.4 一般约束问题

一般约束问题（含不等式和等式约束）

$$\begin{array}{ll} \min & f({x}) \\ \text { s. t. } & g_{i}({x}) \geqslant 0, \quad i=1, \cdots, m,\\ & h_{j}({x}) \geqslant 0, \quad j=1, \cdots, l. \end{array}$$

• 正则点

  设 $\bar{x}$ 为可行点，不等式约束中在 $\bar{x}$ 起作用约束下标集记作 $I$ ，如果向量组 $\left\{\nabla g_{i}(\bar{x}), \nabla h_{j}(\bar{x}) \mid i \in I, j=1,2, \cdots, l\right\}$ 线性无关，就称 $\bar{x}$ 为约束 $g(x)\ge 0$ 和 $h(x)=0$ 的正则点。

• 可行曲线与切平面（为描述等式约束的可行移动引入）

  • 定义 7.2.4 点集 $\left\{x=x(t) \mid t_{0} \leqslant t \leqslant t_{1}\right\}$ 称为超曲面 $S=\{x|h(x)=0\}$ 上的一条曲线， 若对所有的 $t\in[t_0,t_1]$ 均有$h(x)=0$ ，则如果导数 $x'(t)=\frac{\mathrm dx(t)}{\mathrm dt}$ 存在，则称曲线是可微的，该一阶导数是曲线在点 $x(t)$ 处的切向量，曲面 $S$ 在点 $x$ 处所有可微切向量组成的集合，称为曲面 $S$ 在点 $x$ 的切平面，记作 $T(x)$。

• 等式约束的几何表示

  设 $\bar{x}$ 为曲面 $S=\{x|h(x)=0\}$ 上一个正则点，则在点 $\bar{x}$ 切平面 $T(\bar{x})$ 等于子空间 $H=\left\{d \mid \nabla h(\bar{x})^{\top} d=0\right\}$.

• 定理 7.2.7 一般约束问题最优解的一阶必要条件 —— 几何表示

  设 $\bar{x}$ 为可行点，$I=\{i|g_i(\bar{x})=0\}$， $f,g_i\in I$ 在点 $\bar{x}$ 处可微，$g_i(x)(i\notin I)$ 在 $\bar{x}$ 连续，$h_j(j=1,2,\cdots,l)$ 在点 $\bar{x}$ 连续可微，$\nabla h_j(\bar{x})(j=1,2,\cdots,l)$ 线性无关， 若 $\bar{x}$ 是局部最优解，则在 $\bar{x}$ 处，有

  $$F_{0} \cap G_{0} \cap H_{0}=\varnothing$$

  其中，$F_{0},G_{0},H_{0}$ 的定义为

  $$\begin{aligned} &F_{0}=\left\{{d} \mid \nabla f(\bar{x})^{\mathrm{T}} d<0\right\}, \\ &G_{0}=\left\{{d} \mid \nabla g_{i}(\bar{x})^{\mathrm{T}} {d}>0, i \in I\right\} \\ &H_{0}=\left\{{d} \mid \nabla h_{j}(\bar{x})^{\mathrm{T}} d=0, j=1,2, \cdots, l\right\}. \end{aligned}$$

• 定理 7.2.8 （Fritz John条件） —— 代数表示

  设 $\bar{x}$ 为可行点，$I=\{i|g_i(\bar{x})=0\}$， $f,g_i\in I$ 在点 $\bar{x}$ 处可微，$g_i(x)(i\notin I)$ 在 $\bar{x}$ 连续，$h_j(j=1,2,\cdots,l)$ 在点 $\bar{x}$ 连续可微，若 $\bar{x}$ 是局部最优解，则存在不全为零的数 $w_0,w_i(j\in I)$ 和 $v_j(j=1,2,\cdots,l)$ ，使得

  $$w_{0} \nabla f(\bar{x})-\sum_{i \in I} w_{i} \nabla g_{i}(\bar{x})-\sum_{j=1}^{i} v_{j} \nabla h_{j}(\bar{x})=\mathbf{0}, \quad w_{0}, w_{i} \geqslant 0, \quad i \in I .$$

• 定理 7.2.9 （Kuhn-Tucker 条件）—— K-T条件，在Fritz John条件基础上增加了起约束作用的梯度线性无关的约束规格（对约束条件的限制），以避免出现 $w_0=0$ 的情形。

  设 $\bar{x}$ 为可行点，$I=\{i|g_i(\bar{x})=0\}$， $f,g_i\in I$ 在点 $\bar{x}$ 处可微，$g_i(x)(i\notin I)$ 在 $\bar{x}$ 连续，$h_j(j=1,2,\cdots,l)$ 在点 $\bar{x}$ 连续可微，向量集

  $$\left\{\nabla g_{i}(\bar{x}), \nabla h_{j}(\bar{x}) \mid i \in I, j=1, \cdots, l\right\}$$

  线性无关，若 $\bar{x}$​ 是局部最优解，则存在数 $w_i(j\in I)$​ 和 $v_j(j=1,2,\cdots,l)$​ ，使得

  $$\nabla f(\bar{x})-\sum_{i \in I} w_{i} \nabla g_{i}(\bar{x})-\sum_{j=1}^{i} v_{j} \nabla h_{j}(\bar{x})=\mathbf{0}, \quad w_{i} \geqslant 0, \quad i \in I .$$

  若 $g_i(x)(i\notin I)$ 在点 $\bar{x}$ 处可微，K-T 条件可等价表示为

  $$\begin{aligned} &\nabla f(\bar{x})-\sum_{i=1}^{m} w_{i} \nabla g_{i}(\bar{x})-\sum_{j=1}^{t} v_{j} \nabla h_{j}(\bar{{x}})=\mathbf{0} \\ &w_{i} g_{i}(\bar{x})=0, \quad i=1, \cdots, m \\ &w_{i} \geqslant 0, \quad i=1, \cdots, m, \end{aligned}$$

• 广义 Lagrange 函数

  $$L({x}, {w}, {v})=f({x})-\sum_{i=1}^{m} w_{i} g_{i}({x})-\sum_{j=1}^{l} v_{j} h_{j}({x})$$

  若 $\bar{x}$ 是局部最优解，则存在 Lagrange 乘子 $\bar{w}\ge 0$ 和 $v$ ，使得

  $$\nabla_{x} L(\bar{x}, \bar{w}, \bar{v})=0$$

  此时一般约束问题的一阶必要条件可表示为

  $$\begin{aligned} &\nabla_{x} L({x}, {w}, {v})=\mathbf{0}, \\ &g_{i}({x}) \geqslant 0, \quad i=1, \cdots, m, \\ &h_{j}({x})=0, \quad j=1, \cdots, l, \\ &w_{i} g_{i}({x})=0, \quad i=1, \cdots, m, \\ &w_{i} \geqslant 0, \quad i=1, \cdots, m . \end{aligned}$$

• 定理 7.2.10 凸优化问题最优解的充分条件

  设问题中 $f$ 是凸函数，$g_i(i=1,2,\cdots,m)$ 是凹函数（注意不等式约束 $g_i$ 的符号（若是 $g_i\le0$ ，则应该是凸函数）$h_j(j=1,2,\cdots,l)$ 是线性函数，$S$ 是可行域，$\bar{x}\in S$，$I=\{i|g_i(\bar{x})=0\}$，且在 $\bar{x}$ 处 K-T 条件成立，即存在 $w_i\ge 0(i\in I)$ 及 $v_j(j=1,2,\cdots,l)$ ，使得

  $$\nabla f(\bar{x})-\sum_{i \in I} w_{i} \nabla g_{i}(\bar{x})-\sum_{j=1}^{i} v_{j} \nabla h_{j}(\bar{x})=\mathbf{0}, \quad w_{i} \geqslant 0, \quad i \in I .$$

  则 $\bar{x}$ 为全局最优解。

  注：此处关于函数凸性的假设还可以适当放宽，涉及到准凸和伪凸的概念。

• 切锥

  设 $S$ 是 $\mathbb{R}^{”}$ 中一个非空集合, 点 $\overline{\boldsymbol{x}} \in \mathrm{cl} S$, 集合 $T=\left\{\boldsymbol{d} \mid\right.$ 存在 ${x}^{(k)} \in S, {x}^{(k)} \rightarrow \bar{{x}}$ 及 $\lambda_{k}>0$, 使得 $\left.{d}=\lim _{k \rightarrow \infty} \lambda_{k}\left({x}^{(k)}-\bar{{x}}\right)\right\}$, 则称 ${T}$ 为集合 $S$ 在点 $\bar{{x}}$ 的切锥.

  

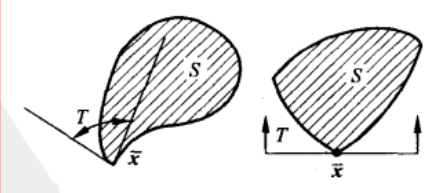
• 定理 7.2.11 （二阶必要条件）

  设 $\bar{x}$ 是局部最优解，$f,g_i,h_j$ 二次连续可微，并存在满足一阶必要条件的乘子 $\bar{w}$ 和 $\bar{v}$ ，再假设在点 $\bar{x}$ 约束规格 $\bar{G}=\bar{T}$ 成立，则对每一个向量 $d\in G$，都有

  $$d^{\mathrm{T}} {\nabla}_{x}^{2} L(\bar{x}, \bar{w}, \bar{v}) {d} \geqslant 0$$

  其中，

  $$\nabla_{x_{x}^{2}}^{2} L(\bar{x}, \bar{w}, \bar{v})=\nabla^{2} f(\bar{x})-\sum_{i=1}^{m} \bar{w}_{i} \nabla^{2} g_{i}(\bar{x})-\sum_{j=1}^{1} \bar{v}_{j} \nabla^{2} h_{j}(\bar{{x}})$$

  是 Lagrange 函数 $L(x,w,v)$ 在 $\bar{x}$ 关于 $x$ 的 Hesse 矩阵。

  集合 $\bar G$ 为

  $$\bar{G}=\left\{d\left | \begin{array}{ll} {d} \in \mathbb{R}^{n} \\ \nabla g_{i}(\bar{x})^{\mathrm{T}} {d}=0, & i \in I \text { 且 } \bar{w}_{i}>0 \\ \nabla g_{i}(\bar{x})^{\mathrm{T}} {d} \geqslant 0, & i \in I \text { 且 } \bar{w}_{i}=0 \\ \nabla h_{j}(\bar{x})^{\mathrm{T}} {d}=0, & j=1, \cdots, l \end{array}\right\}\right.$$

• 定理 7.2.12 （二阶充分条件）

  设 $f,g_i,h_j$ 二次连续可微， $\bar{x}$ 是可行点，并存在乘子 $\bar{w}$ 和 $\bar{v}$ 满足一阶必要条件，且对每一个向量 $d\in G$​，都有

  $$d^{\mathrm{T}} {\nabla}_{x}^{2} L(\bar{x}, \bar{w}, \bar{v}) {d}>0$$

  则 $\bar{x}$ 是严格局部最优解。

  其中，集合 $G$ 为

  $$\bar{G}=\left\{d\left | \begin{array}{ll} d\ne 0\\ \nabla g_{i}(\bar{x})^{\mathrm{T}} {d}=0, & i \in I \text { 且 } \bar{w}_{i}>0 \\ \nabla g_{i}(\bar{x})^{\mathrm{T}} {d} \geqslant 0, & i \in I \text { 且 } \bar{w}_{i}=0 \\ \nabla h_{j}(\bar{x})^{\mathrm{T}} {d}=0, & j=1, \cdots, l \end{array}\right\}\right.$$

  • 注意：对于含等式约束优化问题的二阶极值条件，不能仅考虑 Hesse 矩阵，即便 Hesse 矩阵正定，也不一定是局部最优解。

参考链接

• 《最优化理论与算法》（第7章 最优性条件） 陈宝林著