对偶理论
对偶问题的意义在于无论原问题是凸还是非凸,对偶问题都是凸优化问题。通过将原问题转化为对偶问题,有将复杂问题简单化的可能性,并能够求得原问题的全局最优解。
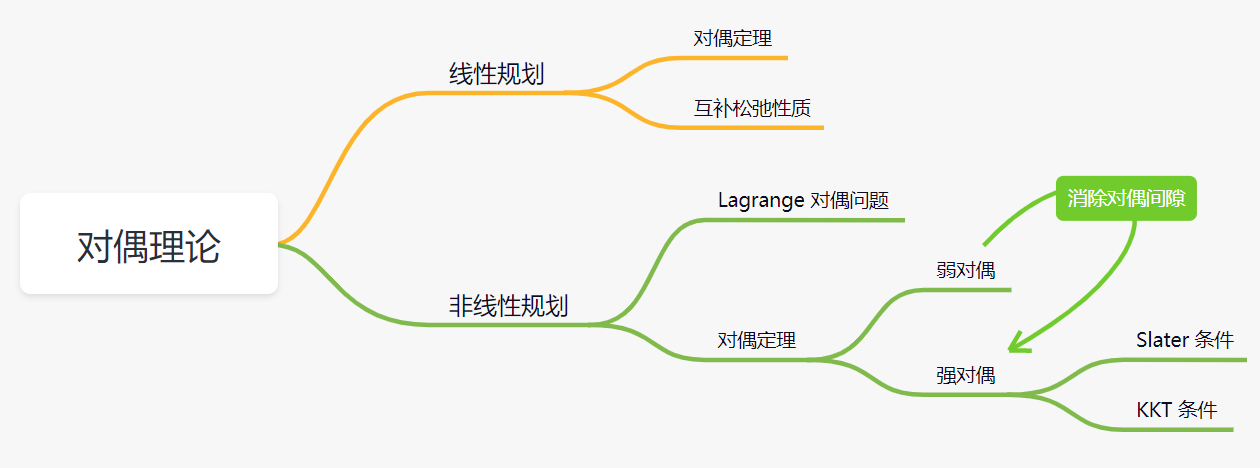
一、线性规划中的对偶理论
1.1 对偶的三种形式
-
对称形式的对偶(只包含不等式约束)
原问题
\[\begin{array}{ll} \min & c x \\ \text { s. t. } & A x \geqslant b,\\ & x \geqslant 0 . \end{array}\quad\quad(1) \]对偶问题
\[\begin{array}{ll} \max & w b \\ \text { s. t. } & w A \leqslant c,\\ & w \geqslant 0 . \end{array}\quad\quad(2) \]其中,\(A=(p_1,p_2,\cdots,p_n)\) 是 \(m\times n\) 矩阵,\(b=(b_1,b_2,\cdots,b_m)\) 是 \(m\) 维列向量,\(c=(c_1,c_2,\cdots,c_n)\) 是 \(n\) 维行向量,\(x=(x_1,x_2,\cdots,x_n)\) 是由原问题的变量组成的 \(n\) 维列向量,\(w=(w_1,w_2,\cdots,w_m)\) 是由对偶问题的变量组成的 \(m\) 维行向量。(原问题约束条件个数=对偶问题中变量的个数;原问题中变量个数=对偶问题中约束条件的个数)
-
非对称形式的对偶(只包含等式约束)
原问题
\[\begin{array}{ll} \min & c x \\ \text { s. t. } & A x=b, \\ & x \geqslant 0 \end{array}\quad\quad(3) \]需要先写成等价形式
\[\begin{array}{ll} \min & c x \\ \text { s. t. } & A x\ge b, \\ &-A x\le -b, \\ & x \geqslant 0 \end{array}\quad\quad(4) \]对偶问题
\[\begin{array}{ll} \max & wb \\ \text { s. t. } & wA \le c. \end{array}\quad\quad(5) \]其中,对偶问题中的变量无正负号限制。
-
一般情形
原问题
\[\begin{array}{ll} \min & {c x} \\ \text { s. t. } & {A}_{1} {x} \geqslant {b}_{1}, \\ & {A}_{2} {x}={b}_{2}, \\ & {A}_{3} {x} \leqslant {b}_{3}, \\ & {x} \geqslant {0} \end{array}\quad\quad(6) \]引入松弛变量将其写成等价形式
\[\begin{array}{ll} \min & {c x} \\ \text { s. t. } & {A}_{1} {x} -x_s = {b}_{1}, \\ & {A}_{2} {x}={b}_{2}, \\ & {A}_{3} {x}+x_t = {b}_{3}, \\ & x,x_s,x_t \geqslant {0} \end{array}\quad\quad(7) \]对偶问题为
\[\begin{array}{ll} \max & {w}_{1} {b}_{1}+{w}_{2} {b}_{2}+{w}_{3} {b}_{3} \\ \text { s. t. } & {w}_{1} {A}_{1}+{w}_{2} {A}_{2}+{w}_{3} {A}_{3} \leqslant {c}, \\ & {w}_{1} \geqslant {0}, \\ & {w}_{3} \leqslant {0}, \\ & {w}_{2} \text { 无限制 , } \end{array}\quad\quad(8) \]
1.2 对偶变换规则
- 若原问题是极大化问题, 那么对偶问题就是极小化问题;若原问题是极小化问 题,那么对偶问题就是极大化问题。
- 在原问题和对偶问题中,约束右端向量与目标函数中系数向量恰好对换。
- 对于极小化问题的“\(\ge\)”型约束(极大化问题中的“\(\le\)”型约束),相应的对偶问题有非负限制;对于极小化问题的“ \(\le\) ”型约束(极大化问题中的“\(\ge\)”型约束),相应的对偶变量有非正制;对于原问题中的“\(=\)”型约束,相应的对偶变量无正负限制。
- 对于极小化问题的具有非负限制的变量(极大化问题的具有非正限制的变量),在其对偶问题中,相应的约束为“ \(\le\) ”型不等式;对极小化问题中具有非正限制的变量(极大化问题的具有非负限制的变量),在其对偶问题中,相应的约束为“\(\ge\)”型不等式;对于原问题中无正负限制的变量, 在其对偶问题中, 相应的约束为等式。
例子

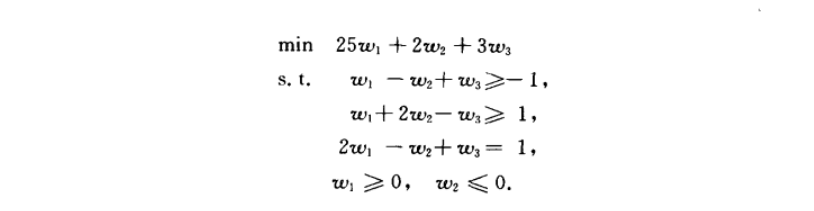
1.3 对偶定理
-
定理 4.1.1 设 \(x^{(0)}\) 和 \(w^{(0)}\) 分别是问题 \((1)\) 和 \((2)\) 的可行解,则 \(cx^{(0)}\ge w^{(0)}b\).
即极小化问题给出极大化问题的目标函数值的上界;极大化问题给出极小化问题的目标函数的下界。
- 推论1:若 \(x^{(0)}\) 和 \(w^{(0)}\) 分别是问题 \((1)\) 和 \((2)\) 的可行解,且\(cx^{(0)}=w^{(0)}b\),则 \(x^{(0)}\) 和 \(w^{(0)}\) 分别是原问题和对偶问题的最优解。
- 推论2:对偶规划 \((1)\) 和 \((2)\) 有最优解的充要条件是它们同时有可行解。
- 推论3:若原问题的目标函数值在可行域无下界,则对偶问题无可行解;反之同理。
-
定理 4.1.2 设原问题和对偶问题中有一个问题存在最优解,则另一个问题也存在最优解,且两个问题的目标函数的最优值相等。
1.4 互补松弛性质
-
定理 4.1.3 设 \(x^{(0)}\) 和 \(w^{(0)}\) 分别是问题 \((1)\) 和 \((2)\) 的可行解,那么 \(x^{(0)}\) 和 \(w^{(0)}\) 都是最优解的充要条件是,对所有的 \(i\) 和 \(j\) ,下列关系成立:
- 若 \(x_{j}^{(0)}>0\),就有 \({w}^{(0)} {p}_{j}=c_{j}\) ;
- 若 \({w}^{(0)} {p}_{j}<c_{j}\),就有 \(x_{j}^{(0)}=0\) ;
- 若 \(w_j^{(0)}>0\),就有 \(A_ix^{(0)}=b_i\) ;
- 若 \(A_ix^{(0)}>b_i\) ,就有 \(w_j^{(0)}=0\) ;
其中,\(p_j\) 是 \(A\) 的第 \(j\) 列,\(A_i\) 是 \(A\) 的第 \(i\) 行。
二、非线性规划中的对偶理论
对偶问题的极大值等于原问题的极小值。这种现象对于线性规划中的对偶是必然的;但是对于非线性规划,这一结论并不是普遍成立。
2.1 共轭函数(对偶函数)
-
定义
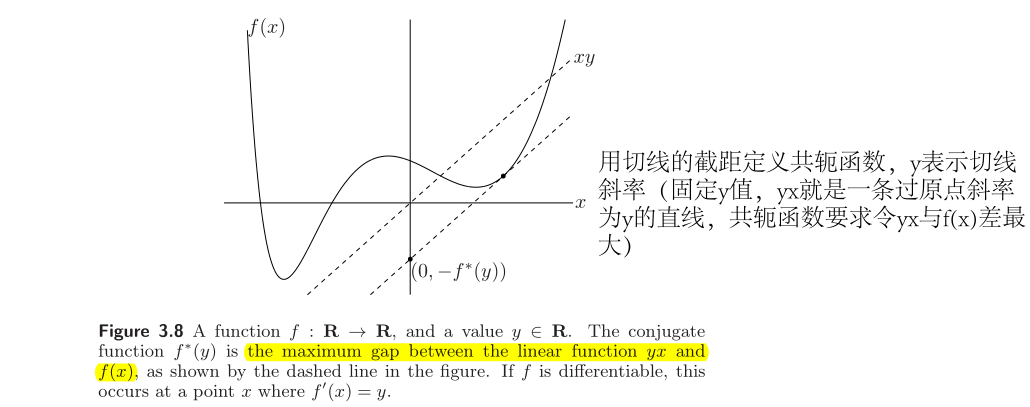
假设 \(f:\mathrm{R}^n\rightarrow \mathrm{R}\),则将其共轭函数定义为 \(f^*:\mathrm{R}^n\rightarrow \mathrm{R}\) ,表示为
\[f^{*}(y)=\sup _{x \in \operatorname{dom} f}\left(y^{T} x-f(x)\right) \]该共轭函数的定义域由 \(y\in\mathrm{R}^n\) 组成,其上确界是有限的。其定义可由下图解释
![conjugate function]()
-
解释
共轭函数 \(f^*\) 实际上是由一系列仿射函数的逐点上确界组成(\(\sup _{x \in \operatorname{dom} f}\left(y^{T} x-f(x)\right)\) 的第一项是关于 \(y\) 的线性函数,第二项无关),由于仿射函数是凸函数,而逐点上确界是保凸运算,因此 \(f^*\) 是凸函数。因此无论原函数 \(f\) 是否为凸,其共轭函数都是凸函数。且仅当 \(f\) 为凸且闭合时,\(f^{**}=f\) 。
-
共轭函数的意义
即便一个函数为非凸函数,也可以通过共轭运算获得一个凸函数以求得其最优解。
2.2 Lagrange 对偶问题
考虑非线性规划问题
则其对偶问题可以写为
称为 Lagrange 对偶问题 。其目标函数 \(\theta(\lambda,\nu)\) 为 Lagrange 对偶函数,其定义如下:
其中,\(L(x, \lambda, \nu)\) 是 Lagrange 函数,\(L\) 称为 Lagrange 算符,\(\lambda, \nu\) 是 Lagrange 乘子。根据 2.1 节所述,由于 Lagrange 对偶函数是一系列仿射函数的逐点下确界,因此 \(\theta(\lambda,\nu)\) 是凹函数,而对偶问题的约束条件为凸集,因此 Lagrange 对偶问题为凸优化问题,且无论原问题是否为凸优化问题。
2.3 对偶定理
-
7.3.1 弱对偶定理 设 \(x\) 和 \((\lambda,\nu)\) 分别是原问题和对偶问题的可行解,则
\[f(x)\ge \theta(\lambda,\nu). \]-
推论1:对于原问题和对偶问题,必有
\[\inf\{f(x)|g(x)\le 0,h(x)=0,x\in D\} \ge \sup\{\theta(\lambda,\nu)|\lambda\ge 0\} \] -
推论2:若 \(f(\overline{x})\le\theta(\overline{\lambda},\overline{\nu})\) ,其中
\[\overline{x}\in\{x|g(x)\le 0,h(x)=0,x\in D\},\overline{\lambda}\ge 0 \]则 \(\overline{x}\) 和 \((\overline{\lambda},\overline{\nu})\) 分别是原问题和对偶问题的最优解。
-
推论3:若
\[\inf\{f(x)|g(x)\le 0,h(x)=0,x\in D\} = -\infty \]则对每个 \(\lambda\ge 0\) ,有 \(\theta(\lambda,\nu)=-\infty\) 。
-
推论4:若
\[\sup\{\theta(\lambda,\nu)|\lambda\ge 0\}=\infty \]则原问题无可行解。
若原问题目标函数最优值为 \(f_{\mathrm{min}}\) ,对偶问题最优值为 \(\theta_{\mathrm{max}}\) ,则必有 \(f_{\mathrm{min}}\ge \theta_{\mathrm{max}}\) ,若严格不等号成立,即 \(f_{\mathrm{min}}> \theta_{\mathrm{max}}\) ,则称存在对偶间隙。为了保证不出现对偶间隙,需要对目标函数和约束函数的性态给予适当的限定,以建立强对偶定理。
-
-
定理7.3.3 强对偶定理 设 \(D\) 是 \(\mathbb{R}^n\) 中的一个非空凸集,\(f\) 和 \(g_i(i=1,2,\cdots,m)\) 是 \(\mathbb{R}^n\) 上的凸函数,\(h_j(j=1,2,\cdots,p)\) 是 \(\mathbb{R}^n\) 上的仿射函数,即 \(h(x)=Ax-b\) ,又设存在点 \(\hat x\in D\),使得
\[g(\hat{x})<0, \quad h(\hat{x})=0, \quad 0 \in \text { int } H(D) \]其中,\(H(D)=\{h(x)|x\in D\}\) ,则
\[\inf\{f(x)|g(x)\le 0,h(x)=0,x\in D\} = \sup\{\theta(\lambda,\nu)|\lambda\ge 0\} \]且若式子中 \(\inf\) 为有限值,则
\[\sup\{\theta(\lambda,\nu)|\lambda\ge 0\} \]在 \((\overline{\lambda},\overline{\nu})\) 处达到,\(\overline{\lambda}\ge 0\) 。如果 \(\inf\) 在点 \(\overline{x}\) 达到,则 \(\overline{\lambda}^\mathrm{T}g(\overline x)=0\) 。
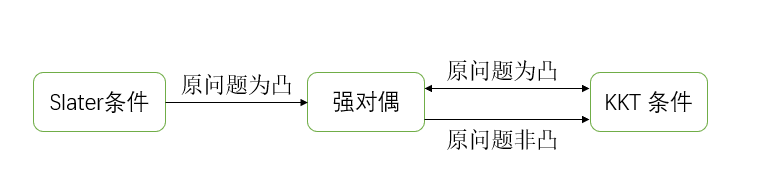
对于凸优化问题,在适当的约束规格下(Slater 条件),原问题的极小值与对偶问题的极大值是相等的。
-
Slater 条件
在原问题是凸优化问题时,Slater 条件是强对偶成立的充分不必要条件。
定义:存在点 \(x\in \mathrm{relint}\;D\) (\(\mathrm{relint}\;D\) 指的是集合 \(D\) 的相对内部,去除边缘的集合,相当于开集),使得
\[g_{i}(x)<0, \quad i=1,2, \ldots, m, \quad h_j=0,\quad j=1,2,\cdots,p \]其中,\(h_j(x)\) 是仿射函数,即 \(h(x)=Ax-b\) 。一般称之满足 Slater 条件的点为严格可行点。
2.4 KKT 条件
-
当原问题和对偶问题满足强对偶时,若 \(x^*\) 和 \((\lambda^*,\nu^*)\) 分别是原问题和对偶问题的最优点,则存在下式
\[\begin{aligned} f\left(x^*\right) &=\theta\left(\lambda^{*}, \nu^{*}\right) \\ &=\inf _{x}\left(f(x)+\sum_{i=1}^{m} \lambda_{i}^{*} g_{i}(x)+\sum_{j=1}^{p} \nu_{j}^{*} h_{j}(x)\right) \\ & \leq f\left(x^{*}\right)+\sum_{i=1}^{m} \lambda_{i}^{*} g_{i}\left(x^{*}\right)+\sum_{j=1}^{p} \nu_{j}^{*} h_{j}\left(x^{*}\right) \\ & \leq f\left(x^{*}\right) . \end{aligned} \]其中,第三行式子代表 \(L(x, \lambda^*, \nu^*)\) 在 \(x^*\) 处取得最小值。
-
互补松弛条件(complementary slackness)
根据该式第三行,可得到
\[\lambda_{i}^{*} g_{i}\left(x^{*}\right)=0, \quad i=1,2, \ldots, m . \]此条件的含义是:要么第 \(i\) 个 Lagrange 乘子为0,要么第 \(i\) 个约束条件有效。因为
\[\begin{aligned} &\lambda_{i}^{*}>0 \Longrightarrow g_{i}\left(x^{*}\right)=0, \\ &\mathrm{or}\\ &g_{i}\left(x^{*}\right)<0 \Longrightarrow \lambda_{i}^{*}=0 . \end{aligned} \] -
Karush-Kuhn-Tucker(KKT)条件
对于非凸问题,若原问题和对偶问题满足强对偶,则一定满足 KKT 条件(KKT 条件是强对偶的必要不充分条件);
对于凸问题,若满足 KKT 条件,则其原问题和对偶问题一定满足强对偶(充要条件)。
\[\begin{aligned} g_{i}\left(x^{*}\right) & \leq 0, \quad i=1,2, \ldots, m \\ h_{j}\left(x^{*}\right) &=0, \quad j=1,2, \ldots, p \\ \lambda_{i}^{*} & \geq 0, \quad i=1,2, \ldots, m \\ \lambda_{i}^{*} g_{i}\left(x^{*}\right) &=0, \quad i=1,2, \ldots, m \\ \nabla f\left(x^{*}\right)+\sum_{i=1}^{m} \lambda_{i}^{*} \nabla g_{i}\left(x^{*}\right)+\sum_{j=1}^{p} \nu_{j}^{*} \nabla h_{j}\left(x^{*}\right) &=0, \end{aligned} \]其中,第 1,2,3 项为原问题和对偶问题的约束条件,第 4 项是互补松弛条件,第 5 项是因为 \(L(x, \lambda^*, \nu^*)\) 在 \(x^*\) 处取得最小值,因此梯度为 0。
-
总结
参考链接
- 《最优化理论与算法》第4章、第7章。陈宝林著
- 《Convex Optimization》
- 整体理解对偶问题,slater,kkt条件
- 简单介绍KKT条件


 浙公网安备 33010602011771号
浙公网安备 33010602011771号