最速下降法、牛顿法、共轭梯度法原理及对比
三者都是基于导数的迭代优化方法,用于求解无约束优化问题。
代码:https://github.com/321hjd/ImageBed/tree/main/code/NumericalOptimization/derivative-basedOptimization
一、最速下降法
1.1 原理
基本思想
-
最速下降法是梯度下降法和一维搜索的结合
-
梯度下降法采用一阶泰勒展开式对函数近似,然后将变量沿着负梯度方向(下降最快的方向)移动一定的步长,目标函数就会一直减小,直至接近极小值
\[\begin{align} &f(x) \approx f\left(x_{0}\right)+\nabla f(x)\left(x-x_{0}\right)\\ &d^{(k)}=-\nabla f(x)\\ &x^{(k)+1}=x^{(k)}+\lambda d^{(k)} \end{align} \] -
步长的确定。让变量在负梯度方向走一段能让函数值最小的距离。可通过求解下式得到(一般通过令其对 \(\lambda\) 求导为0直接求解或通过一维搜索算法如试探法、函数逼近法迭代求解)。
\[\lambda_k=\arg\min _\limits{\lambda \geq 0} f\left(x^{(k)}+\lambda d^{(k)}\right) \] -
一阶收敛条件。梯度的范数满足趋近于0的精度要求
算法步骤
-
步骤1:选取初始点 \(x^0\) ,给定终止精度要求 \(\varepsilon>0\) ,令迭代编号 \(k=0\)
-
步骤2:计算梯度 \(\nabla f(x^k)\) ,若满足 \(||\nabla f(x^k)||<\varepsilon\) ,则停止算法,输出极值点 \(x^k\),否则进入步骤3
-
步骤3:取负梯度 \(d^{(k)}=-\nabla f(x^k)\) 作为下降方向
-
步骤4:一维搜索求最佳步长 \(\lambda_k\) ,使得其满足沿该方向移动步长 \(\lambda_k\) 后,函数值最小
\[\lambda_k=\arg\min _\limits{\lambda \geq 0} f\left(x^{(k)}+\lambda d^{(k)}\right) \] -
步骤5:变量迭代 \(x^{(k+1)}=x^{(k)}+\lambda_k d^{(k)}\) ,回到步骤2继续迭代
算法特点
-
最速下降法的搜索过程是锯齿形的,每一步所得方向(负梯度)都与上一步正交,在远离极值点时收敛速度快,但接近极值点时收敛非常慢(可以和其它在极值点附近收敛速度快的算法结合)
正交的原因:
一维搜索时无论是利用求导直接求解还是一维搜索方法,最终目的都是令其梯度趋近于零。即
\[\frac{\partial f(x^{(k)}-\lambda\nabla f(x^{(k)}))}{\partial \lambda}=-\nabla f(x^{(k)}-\lambda\nabla f(x^{(k)}))\nabla f(x^{(k)})=-\nabla f(x^{(k+1)})\nabla f(x^{(k)})=0 \]内积为0,因此相邻步的方向是正交的。
-
最速下降法所得解是局部最优解,而非全局最优解,仅当目标函数为凸函数时,为全局最优。可形象地解释为:在点x1处向梯度方向到达x2,x2再向梯度方向到达x3,但这不一定是x1到x3最快的路径。
1.2 实例
目标函数:\(f(x_1,x_2)=x_1^2+x_1x_2+3x_2^2\)
初始点:\((1,1)\)
终止精度:\(\mathrm{eps}=10^{-5}\)
等高线及迭代点搜索过程图
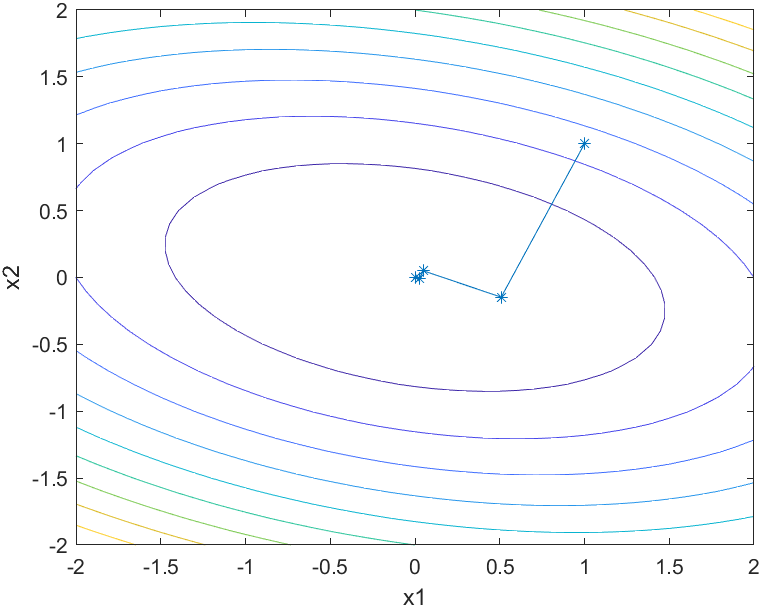
经过9次迭代,算法终止。可以看到在接近极小值点时,最速下降法收敛速度非常慢。
二、牛顿法
2.1 原理
算法思想
-
二阶函数近似。利用二阶泰勒展开式对目标函数进行近似,因此会用到一阶导数(梯度)和二阶导数(海森矩阵)
-
近似极小值点。将近似得到二阶函数的极小值点作为原函数极小值点的近似,并不断重复这一近似的过程,直至得到满足精度要求的极小值点
-
终止条件仍然是满足梯度趋近于0
\[\begin{align} &f(x) \approx f\left(x^{(k)}\right)+\nabla f(x^{(k)})\left(x-x^{(k)}\right)+\frac{1}{2}\nabla^2 f(x^{(k)})\left(x-x^{(k)}\right)^2\\ &f'(x)=\nabla f(x^{(k)})+\nabla^2 f(x^{(k)})\left(x-x^{(k)}\right)=0\\ &x^{(k+1)}=x^{(k)}-\frac{\nabla f(x^{(k)})}{\nabla^2 f(x^{(k)})} \end{align} \]
算法步骤
- 步骤1:选取初始点 \(x^0\) ,给定终止精度要求 \(\varepsilon>0\) ,令迭代编号 \(k=0\)
- 步骤2:计算梯度 \(\nabla f(x^k)\) ,若满足 \(||\nabla f(x^k)||<\varepsilon\) ,则停止算法,输出极值点 \(x^k\),否则进入步骤3
- 步骤3:计算海森矩阵 \(\nabla^2 f(x^k)\)
- 步骤4:变量迭代 \(x^{(k+1)}=x^{(k)}-\frac{\nabla f(x^{(k)})}{\nabla^2 f(x^{(k)})}\) ,并回到步骤2继续迭代
算法特点
-
相比最速下降法,省去了一维搜索的步骤,但需要计算海森矩阵及其逆
-
收敛速度快,具有局部二阶收敛性。形象解释:最速下降法只考虑当前位置下降最快的方向,而不考虑下降后的坡度如何;而牛顿法同时考虑当前下降方向(一阶导)和下降之后坡度的变化(二阶导)
-
对于二次函数(正定二次型),牛顿法具有一步收敛性
假设目标函数为二次型 \(f(x)=\frac{1}{2}x^TQx-x^Tb\)
梯度为:\(\nabla f(x^{(0)})=Qx^{(0)}-b\)
海森矩阵为: \(\nabla^2 f(x^{(0)})=Q\)
经过牛顿法一次迭代后,近似极值点为:\(x^{(1)}=\frac{b}{Q}\)
重新计算梯度: \(\nabla f(x^{(1)})=Qx^{(1)}-b=0\) ,算法终止
2.2 实例
目标函数:\(f(x_1,x_2)=x_1^2+x_1x_2+3x_2^2\)
初始点:\((1,1)\)
终止精度:\(\mathrm{eps}=10^{-5}\)
等高线及迭代点搜索过程图
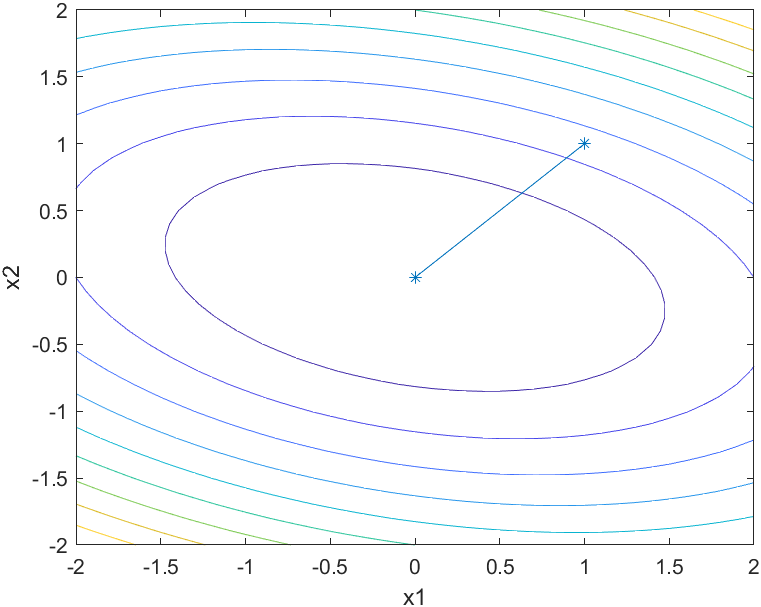
由于牛顿法对于二次函数的一步收敛性,可见仅经过1次迭代,算法终止。
三、共轭梯度法
3.1 原理
术语
-
残差
假设目标函数为二次型 \(f(x)=\frac{1}{2}x^TQx-x^Tb\) ,其中 \(b,x\in\mathbb{R}^n,Q\in\mathbb{R}^{n\times n}\) 且矩阵 \(Q\) 是对称正定的。\(n\) 代表解空间是 \(n\) 维的,即 \(n\) 元二次函数。
其最小值可以通过令一阶导为零得到:\(\nabla f(x^*)=Qx^*-b=0\)
假设通过迭代法求解,迭代法通常无法令该一阶导等于零,因此可将 \(\nabla f(x^{(k)})-\nabla f(x^*)\) 称作系统残差(也是梯度),具体表示为:
\[r^{(k)}=Qx^{(k)}-b \] -
共轭向量
当一组向量 \(\{p_0,p_1,\cdots,p_{n-1}\}\) 满足如下条件时,称其关于对称正定矩阵 \(Q\) 共轭。
\[p_i^TQp_j=0\quad\forall i\ne j \]这样一组向量是线性独立的,可以张成整个空间 \(\mathbb{R}^n\) ,因而可以用来表示其它向量。
算法思想
-
与最速下降法类似,需要找到下降方向(二者的区别也就在于确定的下降方向不同),然后通过一维搜索找到变量 \(x_k\) 迭代的最优步长 \(\lambda_k\)
对于寻找最优步长 \(\lambda_k\) ,需要将
\[x_{k+1}=x_{k}+\lambda p_k \]代入目标函数 \(f(x)\) 并对 \(\lambda\) 求导。因此可以得到:
\[\lambda_k=-\frac{r_k^Tp_k}{p_k^TQp_k} \] -
利用共轭梯度法确定下降方向 \(p_k\)。将最优解点和初始点的差用一组线性无关的共轭向量(向量个数与解空间维度相同)的线性组合近似。然后逐个寻找共轭向量及其系数(步长),构建每一个方向(维度)上的最优解,即沿着解空间的维度逐步构建最优解。具体可解释如下:
将最优解和初始值的差表示为共轭向量的线性组合:
\[x^{*}-x_{0}=\beta_{0} p_{0}+\beta_1 p_1+\ldots+\beta_{n-1} p_{n-1} \]其中 \(\beta_k\) 就是沿着每个共轭向量\(p_k\)(方向)走的步长。对于第 \(k\) 步,\(x_k\) 将 \(x^*\) 投影到由 \(k\) 个线性独立的共轭向量张成的解空间中。
共轭向量 \(p_{k+1}\) 的寻找依赖于负残差和上一个共轭向量。负残差其实就是负梯度,因此称为共轭梯度法。每次迭代找到的新方向(共轭向量)是负残差和上一个搜索方向的线性组合:
\[p_{k+1}=-r_{k+1}+\beta_kp_{k} \]其中,步长 \(\beta_k\) 可以根据共轭条件(\(p_{k}^TQp_{k+1}=0\))得到:
\[\beta_{k}=\frac{r_{k+1}^T Q p_{k}}{p_{k}^{T} Q p_{k}} \] -
\(\lambda_k\) 和 \(\beta_k\) 计算的简化
\[\lambda_k=-\frac{r_k^Tp_k}{p_k^TQp_k}=\frac{r_k^Tr_k}{p_k^TQp_k}\\ \beta_{k}=\frac{r_{k+1}^T Q p_{k}}{p_{k}^{T} Q p_{k}}=\frac{r_{k+1}^{T}r_{k+1} }{r_{k}^{T} r_{k}} \]
对于 \(\lambda_k=\frac{r_k^Tr_k}{p_k^TQp_k}\)
由于 \(p_{k+1}=-r_{k+1}+\beta_kp_{k}\) ,且 \(r_{k+1}^Tp_{k}=0,r_{k+1}r_k=0\)
同时 \(r_{k}=Qx_k-b\)
所以 \(r_{k+1}-r_k=Q(x_{k+1}-x_k)=Q\lambda_kp_k\)
进一步 \(\lambda_k=\frac{r_{k+1}-r_k}{Qp_k}\)
分子分母左乘 \(p_k^T\) 代入即可证明。
对于 \(\beta_k=\frac{r_{k+1}^{T}r_{k+1} }{r_{k}^{T} r_{k}}\)
由1中证明,\(Qp_k=\frac{r_{k+1}-r_k}{\lambda_k},r_{k+1}r_k=0\)
代入可得到分子 \(r_{k+1}^{T}r_{k+1}\)
由 \(p_{k}^Tr_{k+1}=0\) ,所以 \(p_{k}^Tr_{k}=r_{k}^Tr_{k}\)
进一步可得到分母 \(r_{k}^{T}r_{k}\)
算法步骤
-
步骤1:计算初始残差(梯度)\(r_0=Qx_0-b\) ,初始下降方向(负梯度) \(p_0=-r_0\)
-
步骤2:按下列公式迭代 \(k=0,1,\cdots,n-1\) 直到收敛(n维搜索n步)(收敛条件仍然是残差(梯度)满足精度要求)
\[\lambda_k=\frac{r_k^Tr_k}{p_k^TQp_k}\\ x_{k+1}=x_{k}+\lambda p_k\\ r_{k+1}=r_k+\lambda_kQp_k\\ \beta_k=\frac{r_{k+1}^{T}r_{k+1} }{r_{k}^{T} r_{k}}\\ p_{k+1}=-r_{k+1}+\beta_kp_k \]
算法特点
- 仅需计算一阶导数,但收敛速度比最速下降法快;不需要像牛顿法一样存储和计算海森矩阵并求逆
- 具有“步收敛性”,即在每个方向都走到极致,不会走曾经走过的方向,n维空间只需要走n步即可找到极值点。
3.2 实例
目标函数:\(f(x_1,x_2)=x_1^2+x_1x_2+3x_2^2\)
初始点:\((1,1)\)
终止精度:\(\mathrm{eps}=10^{-5}\)
等高线及迭代点搜索过程图
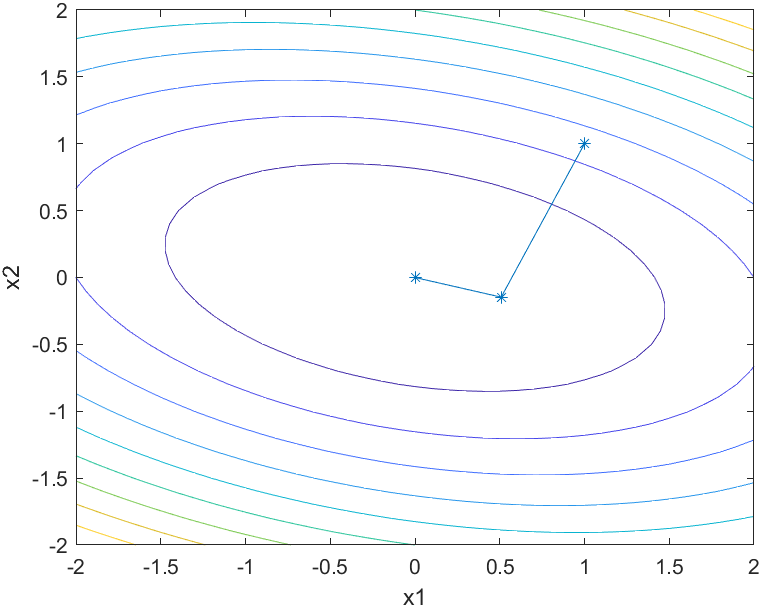
因为是二元函数,可见仅经过2次迭代,算法终止。
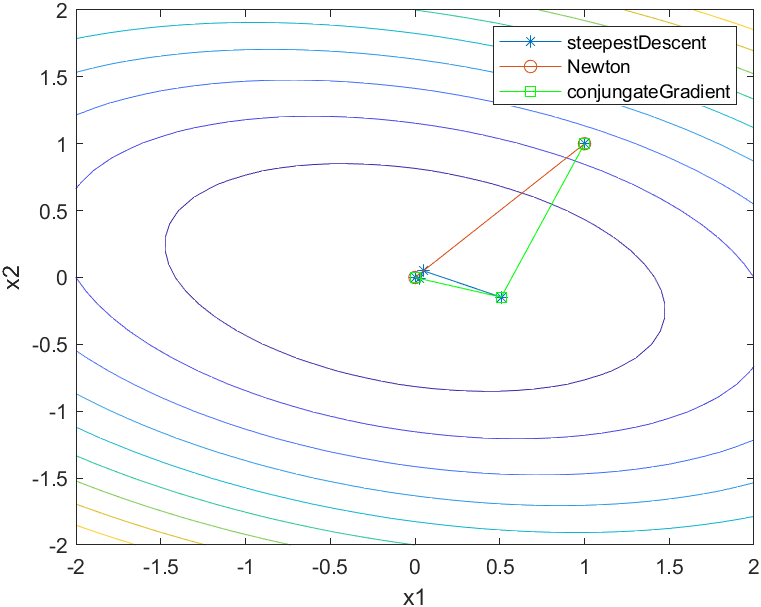
三种方法的搜索过程对比


 浙公网安备 33010602011771号
浙公网安备 33010602011771号