mixup: Beyond Empirical Risk Minimization

这篇论文MIT和FAIR的工作，主要是提出了一种mixup的方式。（感觉是一种产生hard sample的方法，是一种新的、更有效的数据增强。）

1 Introduction

大网络需要大数据，目前CV领域的任务逐渐采用大模型来解决。这些大模型有两个共同特点：①经验风险最小化（ERM)，在训练集上需要训练出比较好的性能，也就是拟合训练数据；②模型规模与数据集规模线性增长，才有可能训出比较好的模型，作者举了几个任务中的模型与数据集来说明这个问题。

可是矛盾的是，众所周知：当模型规模不随着训练数据增加而增加时，ERM才会得到保证。（此处不太明白是啥意思...）

这一矛盾挑战了ERM在神经网络训练中的适用性。一方面ERM会让网络记住训练数据（而不是泛化），即便做了很强的正则化；另一方面，当测试样本取自于训练数据分布之外时，网络的推测会发生剧变（比如对抗样本）。这些都说明了ERM是不利于泛化的。

以上，作者对ERM作了一番批判，主要还是强调overfitting的问题。

 

接着作者引入了data augmentation，从VRM理论角度描述了一下data augmentation是个啥，也就是使训练数据的特征空间{X}的点更丰富，在原始样本附近，按某一分布产生新样本点。随后又告诉大家，目前的data augmentation有两个毛病：①生成的相似样本是属于同一类的（文中描述为data augmentation assumes that the examples in the vicinity share the same class）；②不同类的样本之间的关系没有被建模。（我觉得，大概就是为了后面说mixup做铺垫，目前的data augmentation产生的样本是增强了各个类的样本数量，而没有强化不同类之间的样本区别。）

 

通过以上论述可知，最初的ERM是没有数据增强的，对训练样本完全信赖，并且尽可能拟合之，这就是ERM principle，可是会带来过拟合，显而易见。VRM是产生近邻virtual sample，也就是做了data augmentation，由此一定程度缓解了过拟合，但是也只是一定程度上，因为仍然是ERM原则，因此还是会有过拟合。同时还存在一些其他问题：生成的virtual sample是通过某一个training sample产生的，并且和该training sample共享同一标签，也就是没有不同类、不同training sample之间的互动。由此引出了一种更好的data augmentation方法，也就是通过mixup的方式来产生virtual sample。

 

 2 From Empirical Risk Minimization to mixup

首先从数据分布角度给出期望风险的形式化定义：feature vector X和target vector Y满足联合分布P(X, Y)，那么期望风险就是所有(X, Y)的Loss function对P(X, Y)的积分。

不幸的是，期望风险是可望而不可即的，只能用经验风险代替。由于各种场景的测试数据的联合分布P是不可知的，只能使用训练数据的分布代替，称为经验分布，使用以各个样本点为中心的Dirac function的平均来计算。那么经验风险所有样本的Loss对经验分布的积分，也即所有样本的Loss直接求平均。对经验风险进行优化，就是ERM（Empirical Risk Minimization）。

由此引出了ERM，为了实现ERM，就要对每一个样本降Loss，因此模型会尽力拟合尽可能多的样本，作者称之为“Memorize”，这和“Generalize”相对。由此导致了训练出来的X与Y之间的映射f在training data之外的表现不好。

为了缓解在原始训练集上ERM带来的过拟合问题，出现了data augmentation，对此的理论解释是VRM。神经网络的本质是特征提取+分类，训练过程是在做两件事：①调节extractor的参数用来提取对分类最有效的特征，②调节classifier的参数用来实现特征空间到target空间的最佳映射。过拟合问题就是：网络对于见过的数据，能够有很大把握分类正确，可是没见过的数据很有可能分类错误，也就是——feature空间到target空间的映射还有Achilles‘ heel。通过data augmentation，可以减少一部分盲区。而VRM就是描述feature空间中样本点附件的空间应该如何划分的问题，VRM通过按照某一分布在真实样本点附近构造virtual sample。

 

鉴于ERM的过拟合严重，VRM还不够general，作者提出了一种数据增强的方式——mixup。其形式非常显然，唯一的包装是vicinal distribution的描述，但是其本质还是很清楚简单的，这就是作者说的Occam's razor。

在实现上，作者提供了一些深入思考：

• 更多数量的样本进行mixup不会带来更多收益。
• 作者的实验是在同一个minibatch中进行mixup，但是注意需要shuffle。
• 同类样本的mixup不会带来收益。

接着在What is mixup doing?部分，作者mixup会让模型behave linearly in-between training examples，这种线性的组合方式会抑制模型做预测时的波动，

 

λ～B(α，α)，作者实验发现，α∈[0.1, 0.4]会使得模型性能相比较ERM提升，过大的α会导致欠拟合。由于mixup后样本数量会增加，因此训练时间要放长，才能使模型得到收敛，性能稳定提升。

 

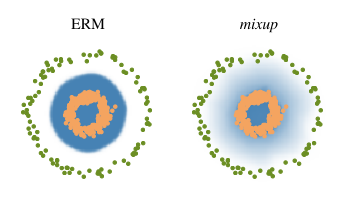
作者给出了一副很形象的示意图，ERM会在各个类之间形成明确的决策边界，而mixup在样本点附近是渐变的，是一种线性过渡。

 

神经网络训练的最终目标是：网络对任何输入数据都能给出正确的预测。这意味着，对于任意的未知数据，网络都要保持鲁棒。如果能够达到这个目的，即使网络在训练集上表现不好也没关系。但是，往往，一个好的模型，在任意输入上表现都好，因此对于训练数据的表现也应该好。训练过程中肯定存在这种问题：网络对训练数据表现越来越好，但训练过程中我们不知道网络有没有出现过拟合。因此，需要一些技术，来预防模型在训练集上出现过拟合，比如regularization、dropout、data augmentation等，mixup的提出也是为了防止过拟合。

 

Previews：

Joint distribution (https://blog.csdn.net/tiankong_/article/details/78332666),

Dirac function (https://zh.wikipedia.org/zh-cn/%E7%8B%84%E6%8B%89%E5%85%8B%CE%B4%E5%87%BD%E6%95%B0),

Beta distribution (https://www.zhihu.com/question/30269898)