机器学习常用模型

（原作：MSRA刘铁岩著《分布式机器学习：算法、理论与实践》。这一部分叙述很清晰，适合用于系统整理NN知识）

 

线性模型

线性模型是最简单的，也是最基本的机器学习模型。其数学形式如下：g(X;W)=W^TX。有时，我们还会在W^TX的基础上额外加入一个偏置项b，不过只要把X扩展出一维常数分量，就可以把带偏置项的线性函数归并到W^TX的形式之中。线性模型非常简单明了，参数的每一维对应了相应特征维度的重要性。但是很显然，线性模型也存在一定的局限性。

 

首先，线性模型的取值范围是不受限的，依据w和x的具体取值，它的输出可以是非常大的正数或者非常小的负数。然而，在进行分类的时候，我们预期得到的模型输出是某个样本属于正类（如正面评价）的可能性，这个可能性通常是取值在0和1之间的一个概率值。为了解决这二者之间的差距，人们通常会使用一个对数几率函数对线性模型的输出进行变换，得到如下公式：

  

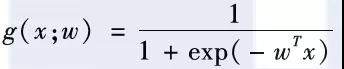
经过变换，严格地讲，g(x;w)已经不再是一个线性函数，而是由一个线性函数派生出来的非线性函数，我们通常称这类函数为广义线性函数。对数几率模型本身是一个概率形式，非常适合用对数似然损失或者交叉熵损失进行训练。

 

其次，线性模型只能挖掘特征之间的线性组合关系，无法对更加复杂、更加强大的非线性组合关系进行建模。为了解决这个问题，我们可以对输入的各维特征进行一些显式的非线性预变换（如单维特征的指数、对数、多项式变换，以及多维特征的交叉乘积等），或者采用核方法把原特征空间隐式地映射到一个高维的非线性空间，再在高维空间里构建线性模型。

 

核方法与支持向量机

略

 

决策树与Boosting

略

 

神经网络

神经网络是一类典型的非线性模型，它的设计受到生物神经网络的启发。人们通过对大脑生物机理的研究，发现其基本单元是神经元，每个神经元通过树突从上游的神经元那里获取输入信号，经过自身的加工处理后，再通过轴突将输出信号传递给下游的神经元。当神经元的输入信号总和达到一定强度时，就会激活一个输出信号，否则就没有输出信号(如图2.7a所示)。

 

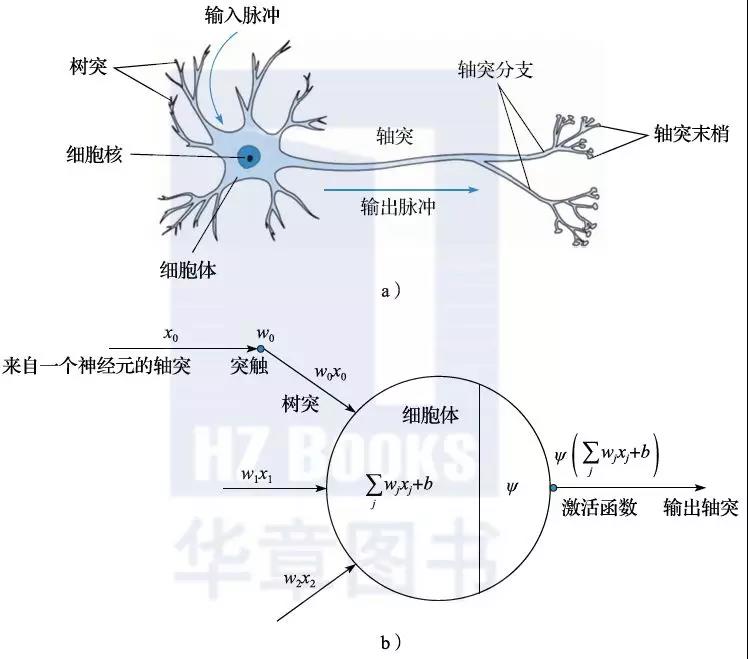
图2.7 神经元结构与人工神经网络

 

这种生物学原理如果用数学语言进行表达，就如图2.7b所示。神经元对输入的信号进行线性加权求和，然后依据求和结果的大小来驱动一个激活函数ψ，用以生成输出信号。生物系统中的激活函数类似于阶跃函数：

 

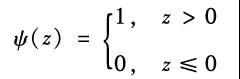
但是，由于阶跃函数本身不连续，对于机器学习而言不是一个好的选择，因此在人们设计人工神经网络的时候通常采用连续的激活函数，比如Sigmoid函数、双曲正切函数(tanh)、校正线性单元(ReLU)等。它们的数学形式和函数形状分别如图2.8所示。

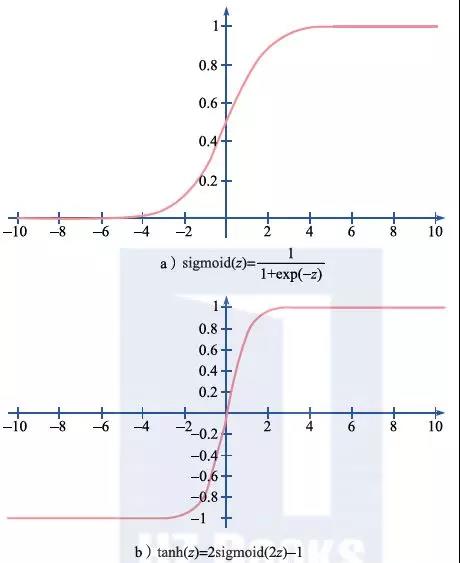
图2.8 常用的激活函数

 

1.全连接神经网络

最基本的神经网络就是把前面描述的神经元互相连接起来，形成层次结构（如图2.9所示），我们称之为全连接神经网络。对于图2.9中这个网络而言，最左边对应的是输入节点，最右边对应的是输出节点，中间的三层节点都是隐含节点（我们把相应的层称为隐含层）。每一个隐含节点都会把来自上一层节点的输出进行加权求和，再经过一个非线性的激活函数，输出给下一层。而输出层则一般采用简单的线性函数，或者进一步使用softmax函数将输出变成概率形式。

 

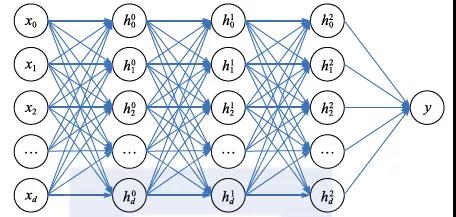
图2.9 全连接神经网络

 

全连接神经网络虽然看起来简单，但它有着非常强大的表达能力。早在20世纪80年代，人们就证明了著名的通用逼近定理(Universal Approximation Theorem[28])。最早的通用逼近定理是针对Sigmoid激活函数证明的，一般情况下的通用逼近定理在2001年被证明[29]。其数学描述是，在激活函数满足一定条件的前提下，任意给定输入空间中的一个连续函数和近似精度ε，存在自然数Nε和一个隐含节点数为Nε的单隐层全连接神经网络，对这个连续函数的L_∞-逼近精度小于ε。这个定理非常重要，它告诉我们全连接神经网络可以用来解决非常复杂的问题，当其他的模型（如线性模型、支持向量机等）无法逼近这类问题的分类界面时，神经网络仍然可以所向披靡、得心应手。近年来，人们指出深层网络的表达力更强，即表达某些逻辑函数，深层网络需要的隐含节点数比浅层网络少很多[30]。这对于模型存储和优化而言都是比较有利的，因此人们越来越关注和使用更深层的神经网络。

 

全连接神经网络在训练过程中常常选取交叉熵损失函数，并且使用梯度下降法来求解模型参数（实际中为了减少每次模型更新的代价，使用的是小批量的随机梯度下降法）。要注意的是，虽然交叉熵损失是个凸函数，但由于多层神经网络本身的非线性和非凸本质，损失函数对于模型参数而言其实是严重非凸的。在这种情况下，使用梯度下降法求解通常只能找到局部最优解。为了解决这个问题，人们在实践中常常采用多次随机初始化或者模拟退火等技术来寻找全局意义下更优的解。近年有研究表明，在满足一定条件时，如果神经网络足够深，它的所有局部最优解其实都和全局最优解具有非常类似的损失函数值[31]。换言之，对于深层神经网络而言，“只能找到局部最优解”未见得是一个致命的缺陷，在很多时候这个局部最优解已经足够好，可以达到非常不错的实际预测精度。

 

除了局部最优解和全局最优解的忧虑之外，其实关于使用深层神经网络还有另外两个困难。

 

• 首先，因为深层神经网络的表达能力太强，很容易过拟合到训练数据上，导致其在测试数据上表现欠佳。为了解决这个问题，人们提出了很多方法，包括DropOut[32]、数据扩张（Data Augmentation）[33]、批量归一化（Batch Normalization）[34]、权值衰减（Weight Decay）[35]、提前终止（Early Stopping）[36]等，通过在训练过程中引入随机性、伪训练样本或限定模型空间来提高模型的泛化能力。

   

• 其次，当网络很深时，输出层的预测误差很难顺利地逐层传递下去，从而使得靠近输入层的那些隐含层无法得到充分的训练。这个问题又称为“梯度消减”问题[37]。研究表明，梯度消减主要是由神经网络的非线性激活函数带来的，因为非线性激活函数导数的模都不太大，在使用梯度下降法进行优化的时候，非线性激活函数导数的逐层连乘会出现在梯度的计算公式中，从而使梯度的幅度逐层减小。为了解决这个问题，人们在跨层之间引入了线性直连，或者由门电路控制的线性通路[38]，以期为梯度信息的顺利回传提供便利。

2.卷积神经网络

除了全连接神经网络以外，卷积神经网络(Convolutional Neural Network，CNN)[13]也是十分常用的网络结构，尤其适用于处理图像数据。

 

卷积神经网络的设计是受生物视觉系统的启发。研究表明每个视觉细胞只对于局部的小区域敏感，而大量视觉细胞平铺在视野中，可以很好地利用自然图像的空间局部相关性。与此类似，卷积神经网络也引入局部连接的概念，并且在空间上平铺具有同样参数结构的滤波器（也称为卷积核）。这些滤波器之间有很大的重叠区域，相当于有个空域滑窗，在滑窗滑到不同空间位置时，对这个窗内的信息使用同样的滤波器进行分析。这样虽然网络很大，但是由于不同位置的滤波器共享参数，其实模型参数的个数并不多，参数效率很高。

 

图2.10描述了一个2×2的卷积核将输入图像进行卷积的例子。所谓卷积就是卷积核的各个参数和图像中空间位置对应的像素值进行点乘再求和。经过了卷积操作之后，会得到一个和原图像类似大小的新图层，其中的每个点都是卷积核在某空间局部区域的作用结果（可能对应于提取图像的边缘或抽取更加高级的语义信息）。我们通常称这个新图层为特征映射（feature map）。对于一幅图像，可以在一个卷积层里使用多个不同的卷积核，从而形成多维的特征映射；还可以把多个卷积层级联起来，不断抽取越来越复杂的语义信息。

 

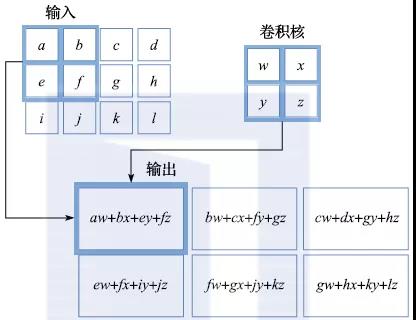
图2.10 卷积过程示意图

 

除了卷积以外，池化也是卷积神经网络的重要组成部分。池化的目的是对原特征映射进行压缩，从而更好地体现图像识别的平移不变性，并且有效扩大后续卷积操作的感受野。池化与卷积不同，一般不是参数化的模块，而是用确定性的方法求出局部区域内的平均值、中位数，或最大值、最小值（近年来，也有一些学者开始研究参数化的池化算子[39]）。图2.11描述了对图像局部进行2×2的最大值池化操作后的效果。

 

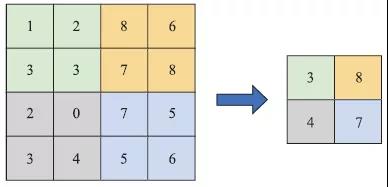
图2.11 池化操作示意图

 

在实际操作中，可以把多个卷积层和多个池化层交替级联，从而实现从原始图像中不断抽取高层语义特征的目的。在此之后，还可以再级联一个全连接网络，在这些高层语义特征的基础上进行模式识别或预测。这个过程如图2.12所示。

 

图2.12 多层卷积神经网络（N1,N2,N3表示对应单元重复的次数）

 

实践中，人们开始尝试使用越来越深的卷积神经网络，以达到越来越好的图像分类效果。图2.13描述了近年来人们在ImageNet数据集上不断通过增加网络深度刷新错误率的历程。其中2015年来自微软研究院的深达152层的ResNet网络[40]，在ImageNet数据集上取得了低达3.57%的Top-5错误率，在特定任务上超越了普通人类的图像识别能力。

 

图2.13 卷积神经网络不断刷新ImageNet数据集的识别结果

 

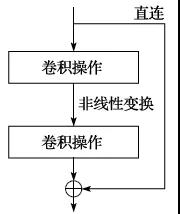
图2.14残差学习

 

随着卷积神经网络变得越来越深，前面提到的梯度消减问题也随之变得越来越显著，给模型的训练带来了很大难度。为了解决这个问题，近年来人们提出了一系列的方法，包括残差学习[40-41]（如图2.14所示）、高密度网络[42]（如图2.15所示）等。实验表明：这些方法可以有效地把训练误差传递到靠近输入层的地方，为深层卷积神经网络的训练奠定了坚实的实践基础。

 

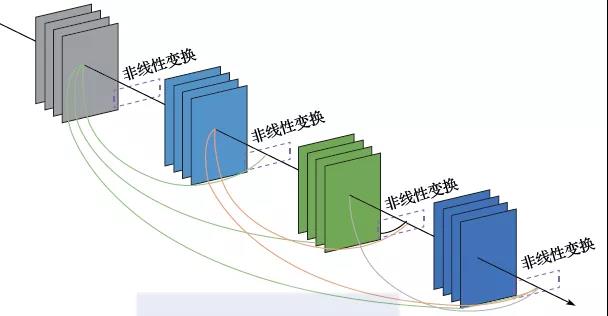
图2.15 高密度网络

 

3.循环神经网络

循环神经网络（Recurrent Neural Network，RNN）[14]的设计也有很强的仿生学基础。我们可以联想一下自己如何读书看报。当我们阅读一个句子时，不会单纯地理解当前看到的那个字本身，相反我们之前读到的文字会在脑海里形成记忆，而这些记忆会帮助我们更好地理解当前看到的文字。这个过程是递归的，我们在看下一个文字时，当前文字和历史记忆又会共同成为我们新的记忆，并对我们理解下一个文字提供帮助。其实，循环神经网络的设计基本就是依照这个思想。我们用表示在时刻的记忆，它是由t时刻看到的输入和时刻的记忆st-1共同作用产生的。这个过程可以用下式加以表示：

 

 

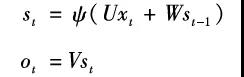
很显然，这个式子里蕴含着对于记忆单元的循环迭代。在实际应用中，无限长时间的循环迭代并没有太大意义。比如，当我们阅读文字的时候，每个句子的平均长度可能只有十几个字。因此，我们完全可以把循环神经网络在时域上展开，然后在展开的网络上利用梯度下降法来求得参数矩阵U、W、V，如图2.16所示。用循环神经网络的术语，我们称之为时域反向传播(Back Propagation Through Time，BPTT)。

 

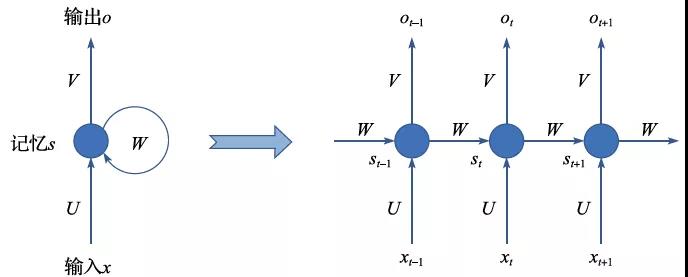
图2.16 循环神经网络的展开

 

和全连接神经网络、卷积神经网络类似，当循环神经网络时域展开以后，也会遇到梯度消减的问题。为了解决这个问题，人们提出了一套依靠门电路来控制信息流通的方法。也就是说，在循环神经网络的两层之间同时存在线性和非线性通路，而哪个通路开、哪个通路关或者多大程度上开关则由一组门电路来控制。这个门电路也是带参数并且这些参数在神经网络的优化过程中是可学习的。比较著名的两类方法是LSTM[43]和GRU[44]（如图2.17所示）。GRU相比LSTM更加简单一些，LSTM有三个门电路（输入门、忘记门、输出门），而GRU则有两个门电路（重置门、更新门），二者在实际中的效果类似，但GRU的训练速度要快一些，因此近年来有变得更加流行的趋势。

 

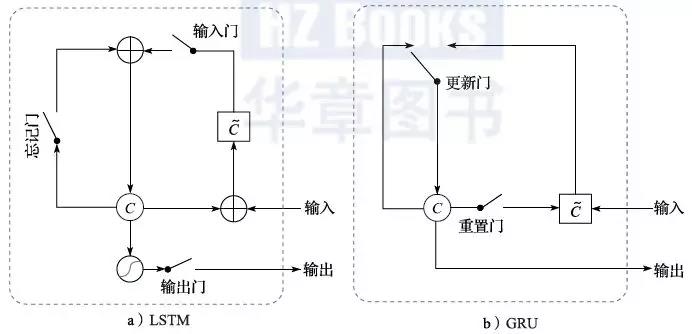
图2.17 循环神经网络中的门电路

 

循环神经网络可以对时间序列进行有效建模，根据它所处理的序列的不同情况，可以把循环神经网络的应用场景分为点到序列、序列到点和序列到序列等类型（如图2.18所示）。

 

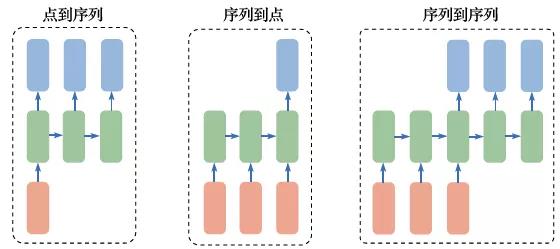
图2.18 循环神经网络的不同应用

 

下面分别介绍几种循环神经网络的应用场景。

 

(1)图像配文字：点到序列的循环神经网络应用

 

在这个应用中，输入的是图像的编码信息（可以通过卷积神经网络的中间层获得，也可以直接采用卷积神经网络预测得到的类别标签），输出则是靠循环神经网络来驱动产生的一句自然语言文本，用以描述该图像包含的内容。

 

(2)情感分类：序列到点的循环神经网络应用

 

在这个应用中，输入的是一段文本信息（时序序列），而输出的是情感分类的标签（正向情感或反向情感）。循环神经网络用于分析输入的文本，其隐含节点包含了整个输入语句的编码信息，再通过一个全连接的分类器把该编码信息映射到合适的情感类别之中。

 

(3)机器翻译：序列到序列的循环神经网络应用

 

在这个应用中，输入的是一个语言的文本（时序序列），而输出的则是另一个语言的文本（时序序列）。循环神经网络在这个应用中被使用了两次：第一次是用来对输入的源语言文本进行分析和编码；而第二次则是利用这个编码信息驱动输出目标语言的一段文本。

 

在使用序列到序列的循环神经网络实现机器翻译时，在实践中会遇到一个问题。输出端翻译结果中的某个词其实对于输入端各个词汇的依赖程度是不同的，通过把整个输入句子编码到一个向量来驱动输出的句子，会导致信息粒度太粗糙，或者长线的依赖关系被忽视。为了解决这个问题，人们在标准的序列到序列循环神经网络的基础上引入了所谓“注意力机制”。在它的帮助下，输出端的每个词的产生会利用到输入端不同词汇的编码信息。而这种注意力机制也是带参数的，可以在整个循环神经网络的训练过程中自动习得。

 

神经网络尤其是深层神经网络是一个高速发展的研究领域。随着整个学术界和工业界的持续关注，这个领域比其他的机器学习领域获得了更多的发展机会，不断有新的网络结构或优化方法被提出。如果读者对于这个领域感兴趣，请关注每年发表在机器学习主流学术会议上的最新论文。

 

参考文献：

［1］Cao Z, Qin T, Liu T Y, et al. Learning to Rank: From Pairwise Approach to Listwise Approach[C]//Proceedings of the 24th international conference on Machine learning. ACM, 2007: 129-136.

［2］Liu T Y. Learning to rank for information retrieval[J]. Foundations and Trends in Information Retrieval, 2009, 3(3): 225-331.

［3］Kotsiantis S B, Zaharakis I, Pintelas P. Supervised Machine Learning: A Review of Classification Techniques[J]. Emerging Artificial Intelligence Applications in Computer Engineering, 2007, 160: 3-24.

［4］Chapelle O, Scholkopf B, Zien A. Semi-supervised Learning (chapelle, o. et al., eds.; 2006)[J]. IEEE Transactions on Neural Networks, 2009, 20(3): 542-542.

［5］He D, Xia Y, Qin T, et al. Dual learning for machine translation[C]//Advances in Neural Information Processing Systems. 2016: 820-828.

［6］Hastie T, Tibshirani R, Friedman J. Unsupervised Learning[M]//The Elements of Statistical Learning. New York: Springer, 2009: 485-585.

［7］Sutton R S, Barto A G. Reinforcement Learning: An Introduction[M]. Cambridge: MIT press, 1998.

［8］Seber G A F, Lee A J. Linear Regression Analysis[M]. John Wiley & Sons, 2012.

［9］Harrell F E. Ordinal Logistic Regression[M]//Regression modeling strategies. New York: Springer, 2001: 331-343.

［10］Cortes C, Vapnik V. Support-Vector Networks[J]. Machine Learning, 1995, 20(3): 273-297.

［11］Quinlan J R. Induction of Decision Trees[J]. Machine Learning, 1986, 1(1): 81-106.

［12］McCulloch, Warren; Walter Pitts (1943). "A Logical Calculus of Ideas Immanent in Nervous Activity" [EB]. Bulletin of Mathematical Biophysics. 5(4): 115-133.

［13］LeCun Y, Jackel L D, Bottou L, et al. Learning Algorithms for Classification: A Comparison on Handwritten Digit Recognition[J]. Neural networks: The Statistical Mechanics Perspective, 1995, 261: 276.

［14］Elman J L. Finding structure in time[J]. Cognitive Science, 1990, 14(2): 179-211.

［15］周志华. 机器学习［M］. 北京：清华大学出版社，2017.

［16］Tom Mitchell. Machine Learning[M]. McGraw-Hill, 1997.

［17］Nasrabadi N M. Pattern Recognition and Machine Learning[J]. Journal of Electronic Imaging, 2007, 16(4): 049901.

［18］Voorhees E M. The TREC-8 Question Answering Track Report[C]//Trec. 1999, 99: 77-82.

［19］Wang Y, Wang L, Li Y, et al. A Theoretical Analysis of Ndcg Type Ranking Measures[C]//Conference on Learning Theory. 2013: 25-54.

［20］Devroye L, Gyrfi L, Lugosi G. A Probabilistic Theory of Pattern Recognition[M]. Springer Science & Business Media, 2013.

［21］Breiman L, Friedman J, Olshen R A, et al. Classification and Regression Trees[J]. 1984.

［22］Quinlan J R. C4. 5: Programs for Machine Learning[M]. Morgan Kaufmann, 1993.

［23］Iba W, Langley P. Induction of One-level Decision Trees[J]//Machine Learning Proceedings 1992. 1992: 233-240.

［24］Breiman L. Bagging predictors[J]. Machine Learning, 1996, 24(2): 123-140.

［25］Schapire R E. The Strength of Weak Learnability[J]. Machine Learning, 1990, 5(2): 197-227. 

［26］Schapire R E, Freund Y, Bartlett P, et al. Boosting the Margin: A New Explanation for The Effectiveness of Voting Methods[J]. Annals of Statistics, 1998: 1651-1686.

［27］Friedman J H. Greedy Function Approximation: A Gradient Boosting Machine[J]. Annals of statistics, 2001: 1189-1232.

［28］Gybenko G. Approximation by Superposition of Sigmoidal Functions[J]. Mathematics of Control, Signals and Systems, 1989, 2(4): 303-314.

［29］Csáji B C. Approximation with Artificial Neural Networks[J]. Faculty of Sciences, Etvs Lornd University, Hungary, 2001, 24: 48.

［30］Sun S, Chen W, Wang L, et al. On the Depth of Deep Neural Networks: A Theoretical View[C]//AAAI. 2016: 2066-2072.

［31］Kawaguchi K. Deep Learning Without Poor Local Minima[C]//Advances in Neural Information Processing Systems. 2016: 586-594.

［32］Srivastava N, Hinton G, Krizhevsky A, et al. Dropout: A Simple Way to Prevent Neural Networks from Overfitting[J]. The Journal of Machine Learning Research, 2014, 15(1): 1929-1958.

［33］Tanner M A, Wong W H. The Calculation of Posterior Distributions by Data Augmentation[J]. Journal of the American statistical Association, 1987, 82(398): 528-540.

［34］ Ioffe S, Szegedy C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift[C]//International Conference on Machine Learning. 2015: 448-456.

［35］Krogh A, Hertz J A. A Simple Weight Decay Can Improve Generalization[C]//Advances in neural information processing systems. 1992: 950-957.

［36］Prechelt L. Automatic Early Stopping Using Cross Validation: Quantifying the Criteria[J]. Neural Networks, 1998, 11(4): 761-767.

［37］Bengio Y, Simard P, Frasconi P. Learning Long-term Dependencies with Gradient Descent is Difficult[J]. IEEE Transactions on Neural Networks, 1994, 5(2): 157-166.

［38］Srivastava R K, Greff K, Schmidhuber J. Highway networks[J]. arXiv preprint arXiv:1505.00387, 2015.

［39］Lin M, Chen Q, Yan S. Network in Network[J]. arXiv preprint arXiv:1312.4400, 2013.

［40］He K, Zhang X, Ren S, et al. Deep Residual Learning for Image Recognition[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2016: 770-778.

［41］He K, Zhang X, Ren S, et al. Identity Mappings in Deep Residual Networks[C]//European Conference on Computer Vision. Springer, 2016: 630-645.

［42］Huang G, Liu Z, Weinberger K Q, et al. Densely Connected Convolutional Networks[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2017, 1(2): 3.

［43］Hochreiter S, Schmidhuber J. Long Short-term Memory[J]. Neural Computation, 1997, 9(8): 1735-1780.

［44］Cho K, Van Merrinboer B, Gulcehre C, et al. Learning Phrase Representations Using RNN Encoder-decoder for Statistical Machine Translation[J]. arXiv preprint arXiv:1406.1078, 2014.

［45］Cauchy A. Méthode générale pour la résolution des systemes d’équations simultanées[J]. Comp. Rend. Sci. Paris, 1847, 25(1847): 536-538.

［46］Hestenes M R, Stiefel E. Methods of Conjugate Gradients for Solving Linear Systems[M]. Washington, DC: NBS, 1952.

［47］Wright S J. Coordinate Descent Algorithms[J]. Mathematical Programming, 2015, 151(1): 3-34.

［48］Polyak B T. Newton’s Method and Its Use in Optimization[J]. European Journal of Operational Research, 2007, 181(3): 1086-1096.

［49］Dennis, Jr J E, Moré J J. Quasi-Newton Methods, Motivation and Theory[J]. SIAM Review, 1977, 19(1): 46-89.

［50］Frank M, Wolfe P. An Algorithm for Quadratic Programming[J]. Naval Research Logistics (NRL), 1956, 3(1-2): 95-110.

［51］Nesterov, Yurii. A method of solving a convex programming problem with convergence rate O (1/k2)[J]. Soviet Mathematics Doklady, 1983, 27(2).

［52］Karmarkar N. A New Polynomial-time Algorithm for Linear Programming[C]//Proceedings of the Sixteenth Annual ACM Symposium on Theory of Computing. ACM, 1984: 302-311.

［53］Geoffrion A M. Duality in Nonlinear Programming: A Simplified Applications-oriented Development[J]. SIAM Review, 1971, 13(1): 1-37.

［54］Johnson R, Zhang T. Accelerating Stochastic Gradient Descent Using Predictive Variance Reduction[C]//Advances in Neural Information Processing Systems. 2013: 315-323.

［55］Sutskever I, Martens J, Dahl G, et al. On the Importance of Initialization and Momentum in Deep Learning[C]//International Conference on Machine Learning. 2013: 1139-1147.

［56］Duchi J, Hazan E, Singer Y. Adaptive Subgradient Methods for Online Learning and Stochastic Optimization[J]. Journal of Machine Learning Research, 2011, 12(7): 2121-2159.

［57］Tieleman T, Hinton G. Lecture 6.5-rmsprop: Divide the Gradient By a Running Average of Its Recent Magnitude[J]. COURSERA: Neural networks for machine learning, 2012, 4(2): 26-31.

［58］Zeiler M D. ADADELTA: An Adaptive Learning Rate Method[J]. arXiv preprint arXiv:1212.5701, 2012.

［59］Kingma D P, Ba J. Adam: A Method for Stochastic Optimization[J]. arXiv preprint arXiv:1412.6980, 2014.

［60］Reddi S, Kale S, Kumar S. On the Convergence of Adam and Beyond[C]// International Conference on Learning Representations, 2018.

［61］Hazan E, Levy K Y, Shalev-Shwartz S. On Graduated Optimization for Stochastic Non-convex Problems[C]//International Conference on Machine Learning. 2016: 1833-1841.