强化学习入门知识与经典项目分析1.4

上一篇文章介绍了策略评估的方法，并且证明了其收敛性，本篇文章在其基础上证明策略迭代、策略提升和价值迭代，并且介绍格子世界的例子

主要的学习资源是四个:

• B站许志钦老师的视频（主要入门理论）https://www.bilibili.com/video/BV15a4y1j7vg?spm_id_from=333.999.0.0
• 书籍《强化学习入门：从原理到实践》（叶强等著，机械工业出版社）
• github中的配套资源 https://github.com/qqiang00/Reinforce
• 书籍《强化学习精要：核心算法与TensorFlow实现》（冯超著，中国工信出版集团）

1.策略迭代

在开始介绍策略迭代之前，我们再回顾一下我们策略评估所完成的事情：
我们在已知一个马尔科夫决策过程\(⟨S, A, P, R, γ⟩\)和一个策略π的情况下，通过贝尔曼方程反复迭代，求解了基于该策略的价值函数\(V_π\)。

我们曾在第一篇文章提到：强化学习的核心思想是通过某种手段影响被实验体的行为，就是说我们希望用手段获得更好的行为。如果用值函数（状态价值函数\(V_π(s)\)和状态行为价值函数\(q_π(s, a)\)合称为值函数）的角度考虑强化学习的目标的话，可以得到：强化学习就是找到最优策略，使每一个状态的价值函数最大化，这相当于求解：

\[π^*=argmax_πV_π(s), \forall s \]

而对于每一个状态对应的行动，我们希望找到使其价值最大化的行动

\[a^*=argmax_aq_{π^*}(s, a) \]

从上面两个式子中我们会发现一个悖论：如果想要知道最优策略，就需要能够准确估计值函数；然而要准确估计值函数，又需要知道最优策略，这样就变成了一个“鸡生蛋、蛋生鸡”的故事。面对这种问题是否可以反复迭代逐渐接近最优结果呢？（这种方法在数值计算领域运用的很多，过段时间我也会写相关的博客介绍。）

于是我们就提出了如下计算思路：

1. 以某种策略π开始，计算当前策略下的值函数\(V_π(s)\)
2. 利用这个值函数，找到更好的策略\(π'\)
3. 用这个策略继续前行，更新值函数，得到\(V'_π(s)\)，然后重复1过程……

上面的计算思路可以用下图的流程表示：

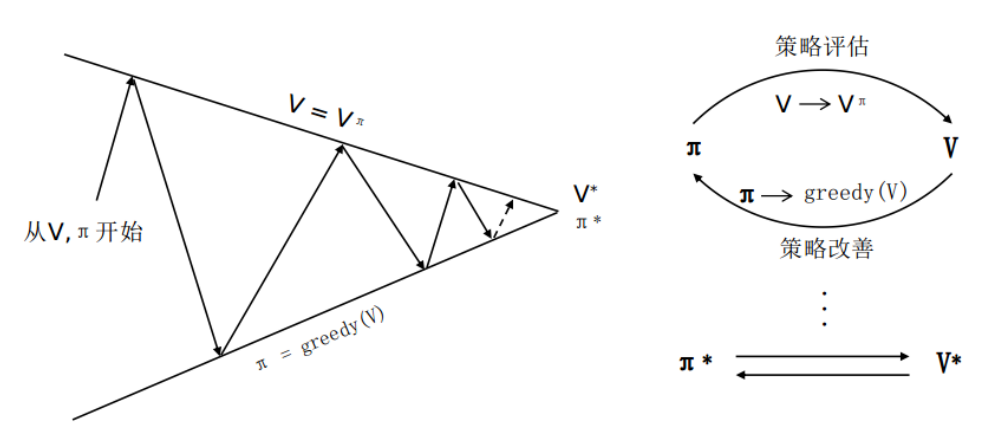
到这里大家肯定发现了：

\[策略迭代=策略评估+策略提升 \]

策略评估这一部分在数学上已经没有问题了，接下来我们需要证明策略提升的可行性。

策略提升及收敛性证明

策略可以分为随机策略和确定性策略， 前者指策略是随机性的，即在一个确定的状态S下可能会概率性地采取不同的行为，\(π(a|s)\)。后者指策略是决定性的，即策略在一个确定的状态S下只可能采取一种行为\(a=π(s)\)。

下文给出基于贪婪策略的迭代将收敛于最优策略和最优状态价值函数的证明。
考虑一个依据确定性策略\(π\)(每个状态后仅跟一个动作)对任意状态\(s\)产生的行为\(a=π(s)\)，贪婪策略在同样的状态\(s\)下会得到新行为\(a′ = π′(s)\)，其中：

\[π'(s)=\underset{a\in A}{argmax}q_π(s,a) \]

假如个体在与环境交互时，仅下一步采取该贪婪策略产生的行为，而在后续步骤仍采取基于原策略产生的行为，那么下面的（不）等式成立

\[q_π(s,π'(s))= \underset{a\in A}{max}q_π(s,a)\ge q_π(s,π(s))=V_π(s) \]

其中上式中的s对状态机S中的所有状态都成立，于是可得下式：

\[\begin{aligned} V_π(s)&\le q_π(s,π'(s))=\sum_{s'}P_{ss'}^a π'(s)[R_{t+1}+γq_π(s',π'(s'))]\\ &\le \sum_{s'}P_{ss'}^a π'(s)R_{t+1}+γ\sum_{s'}P_{ss'}^a π'(s)\sum_{s''}P_{s's''}^{a'}\sum_{a'} π'(s')[R_{t+2}+γq_π(s'',π'(s''))]]\\ &\le ...\\ &\le E[R_{t+1}+γR_{t+2}+···|s_t=s]\\ &=V_{π'}(s) \end{aligned} \]

也就是说，如果使用贪婪策略，新策略下状态价值函数总不劣于原策略下的状态价值函数。

另一方面，我们又可以证明策略提升的收敛性。
每次策略提升时，其计算过程就是如下公式：

\[π(s)=argmax_a (R_s^a+γ\sum_{s'\in S} P_{ss'}^aV(s)) \]

这个公式依据的就是贝尔曼最优方程（虽然我们前面都没有提到过，但很多书都会涉及定义，这边就不赘述了）。
下面是贝尔曼最优方程的收敛性证明：

\[\begin{aligned} d(F(U),F(V))&=||max_a (R+γPU)-max_{a'} (R+γPV)||_\infty\\ &\le || (R+γPU)_a- (R+γPV)_{a}||_\infty\\ &\le γ||U-V||_\infty=γd(U,V) \end{aligned} \]

第一个不等号是说明减号后面减的是满足第一个max的行为a的F(V)，a不一定满足第二个max，所以用\(\le\)。第二个不等号是因为状态转移矩阵\(P\)的每一元素都小于1。
因为前提条件是确定性策略，最优价值函数收敛对应的策略也会收敛，即随着迭代轮数增加，某一状态对应着唯一的行为。

最终我们可以得出完整的策略迭代算法，伪代码如下：

2.价值迭代和融合泛化

如果将下面两个策略迭代关键公式：

\[\begin{cases} V_{k+1}(s) = \sum_aπ(a|s)[R_{s}^a + γ\sum_{s'\in S}P_{ss'}^aV_k(s')]\\ π(s)=argmax_a (R_s^a+γ\sum_{s'\in S} P_{ss'}^aV(s)) \end{cases} \]

整合到一起，就可以得到如下公式：

\[V_{k+1}(s) = \underset{a\in A}{max} [R_{s}^a + γ\sum_{s'\in S}P_{ss'}^aV_k(s')] \]

这个公式实际上是贝尔曼最优方程的迭代表达，我们在上面已经证明了收敛性。
我们可以得出完整的价值迭代算法，伪代码如下：

如果将策略迭代和价值迭代组合使用，我们也可以得到泛化迭代法，这部分冯超老师的书里面有比较详细的说明，这边就不赘述了。

3. 格子世界实例

这部分内容参考了叶强老师的内容，接下来和大家一起欣赏下。

3.1 小型格子世界建模

先对4×4小型方格世界的MDP进行建模，由于4×4方格世界环境简单，环境动力学明确，将不使用字典来保存状态价值、状态转移概率、奖励、策略等。使用列表来描述状态空间和行为空间，编写一个反映环境动力学特征的函数（方法）来确定后续状态和奖励值，该方法接受当前状态和行为作为参数。状态转移概率和奖励也使用函数（方法）的形式来表达。

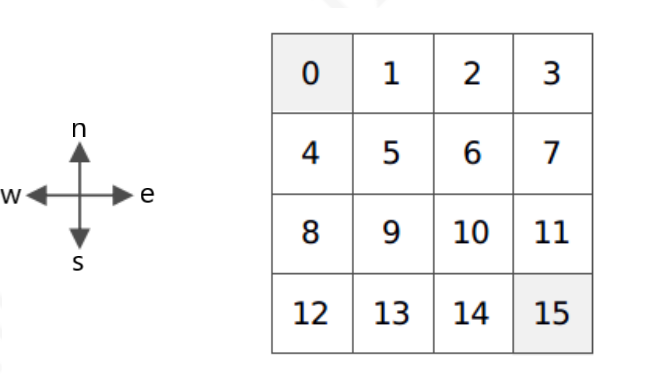
# 4*4 方格状态命名
# 状态0和15为终止状态
#  0  1  2  3
#  4  5  6  7
#  8  9 10  11
# 12 13 14  15
S = [i for i in range(16)] # 状态空间
A = ["n", "e", "s", "w"] # 行为空间
# P,R,将由dynamics动态生成

ds_actions = {"n": -4, "e": 1, "s": 4, "w": -1} # 行为对状态的改变

def dynamics(s, a): # 环境动力学
    模拟小型方格世界的环境动力学特征
    Args:
        s 当前状态 int 0 - 15
        a 行为 str in ['n','e','s','w'] 分别表示北、东、南、西
    Returns: tuple (s_prime, reward, is_end)
        s_prime 后续状态
        reward 奖励值
        is_end 是否进入终止状态
    
    s_prime = s
    if (s%4 == 0 and a == "w") or (s<4 and a == "n") \
        or ((s+1)%4 == 0 and a == "e") or (s > 11 and a == "s")\
        or s in [0, 15]:
        pass
    else:
        ds = ds_actions[a]
        s_prime = s + ds
    reward = 0 if s in [0, 15] else -1
    is_end = True if s in [0, 15] else False
    return s_prime, reward, is_end

def P(s, a, s1): # 状态转移概率函数
    s_prime, _, _ = dynamics(s, a)
    return s1 == s_prime

def R(s, a): # 奖励函数
    _, r, _ = dynamics(s, a)
    return r

gamma = 1.00
MDP = S, A, R, P, gamma

最后建立的MDP同上一个案例一样是一个拥有五元组，只不过R和P都变成了函数而不是字典了。同样变成函数的还有策略。下面的代码分别建立了均一随机策略和贪婪策略，并给出了调用这两个策略的统一的接口。由于生成一个策略所需要的参数并不统一，例如像均一随机策略多数只需要知道行为空间就可以了，而贪婪策略则需要知道状态的价值。为了方便程序使用相同的代码调用不同的策略，于是对参数进行了统一。

def uniform_random_pi(MDP = None, V = None, s = None, a = None):
    _, A, _, _, _ = MDP
    n = len(A)
    return 0 if n == 0 else 1.0/n

def greedy_pi(MDP, V, s, a):
    S, A, P, R, gamma = MDP
    max_v, a_max_v = -float('inf'), []
    for a_opt in A:# 统计后续状态的最大价值以及到达到达该状态的行为（可能不止一个）
        s_prime, reward, _ = dynamics(s, a_opt)
        v_s_prime = get_value(V, s_prime)
        if v_s_prime > max_v:
            max_v = v_s_prime
            a_max_v = [a_opt]
        elif(v_s_prime == max_v):
            a_max_v.append(a_opt)
    n = len(a_max_v)
    if n == 0: return 0.0
    return 1.0/n if a in a_max_v else 0.0

def get_pi(Pi, s, a, MDP = None, V = None):
    return Pi(MDP, V, s, a)

在编写贪婪策略时，考虑了多个状态具有相同最大值的情况，此时贪婪策略将从这多个具有相同最大值的行为中随机选择一个。

3.2 贝尔曼方程构建

为了能使用前一章编写的一些方法，重写一下需要用到的诸如获取状态转移概率、奖励以及显示状态价值等的辅助方法。

# 辅助函数
def get_prob(P, s, a, s1): # 获取状态转移概率
    return P(s, a, s1)

def get_reward(R, s, a): # 获取奖励值
    return R(s, a)

def set_value(V, s, v): # 设置价值字典
    V[s] = v
    
def get_value(V, s): # 获取状态价值
    return V[s]

def display_V(V): # 显示状态价值
    for i in range(16):
        print('{0:>6.2f}'.format(V[i]),end = " ")
        if (i+1) % 4 == 0:
            print("")
    print()

下面一部分和上一个案例类似，就是根据如下的两个公式编写贝尔曼方程函数。

\[q_π(s,a)=R_s^a+γ\sum_{s'\in S}V_{π}(s')P_{ss'}^a \]

\[V_π(s) = \sum_{a\in A}π(a|s)q_π(s,a) \]

def compute_q(MDP, V, s, a):
    '''根据给定的MDP，价值函数V，计算状态行为对s,a的价值qsa
    '''
    S, A, R, P, gamma = MDP
    q_sa = 0
    for s_prime in S:
        q_sa += get_prob(P, s, a, s_prime) * get_value(V, s_prime)
    q_sa = get_reward(R, s,a) + gamma * q_sa
    return q_sa

def compute_v(MDP, V, Pi, s):
    '''给定MDP下依据某一策略Pi和当前状态价值函数V计算某状态s的价值
    '''
    S, A, R, P, gamma = MDP
    v_s = 0
    for a in A:
        v_s += get_pi(Pi, s, a, MDP, V) * compute_q(MDP, V, s, a)
    return v_s        

3.3 策略评估

为了方便起见，就直接n次迭代，也没有作收敛性条件判断（Δ<θ）。

def update_V(MDP, V, Pi):
    '''给定一个MDP和一个策略，更新该策略下的价值函数V
    '''
    S, _, _, _, _ = MDP
    V_prime = V.copy()
    for s in S:
        set_value(V_prime, s, compute_v(MDP, V_prime, Pi, s))
    return V_prime
def policy_evaluate(MDP, V, Pi, n):
    '''使用n次迭代计算来评估一个MDP在给定策略Pi下的状态价值，初始时价值为V
    '''
    for i in range(n):
        #print("====第{}次迭代====".format(i+1))
        V = update_V(MDP, V, Pi)
        #display_V(V)
    return V

下面测试均匀随机策略结果:

V = [0 for _ in range(16)] # 状态价值
V_pi = policy_evaluate(MDP, V, uniform_random_pi, 100)
display_V(V_pi)
#   0.00 -14.00 -20.00 -22.00 
# -14.00 -18.00 -20.00 -20.00 
# -20.00 -20.00 -18.00 -14.00 
# -22.00 -20.00 -14.00   0.00 

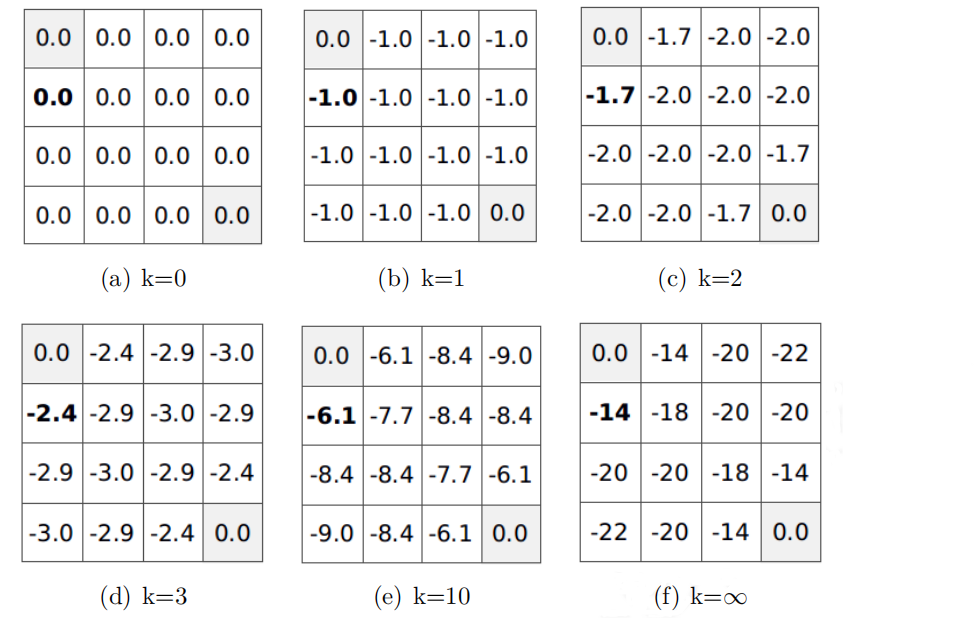
下面测试贪婪策略结果:

V = [0  for _ in range(16)] # 状态价值
V_pi = policy_evaluate(MDP, V, greedy_pi, 100)
display_V(V_pi)

# n=1
#   0.00  -1.00  -1.00  -1.00 
#  -1.00  -1.00  -1.00  -1.00 
#  -1.00  -1.00  -1.00  -1.00 
#  -1.00  -1.00  -1.00   0.00 
# n=2
#   0.00  -1.00  -2.00  -2.00 
#  -1.00  -2.00  -2.00  -2.00 
#  -2.00  -2.00  -2.00  -1.00 
#  -2.00  -2.00  -1.00   0.00 
# n=3
#   0.00  -1.00  -2.00  -3.00 
#  -1.00  -2.00  -3.00  -2.00 
#  -2.00  -3.00  -2.00  -1.00 
#  -3.00  -2.00  -1.00   0.00 
# n=100
#   0.00  -1.00  -2.00  -3.00 
#  -1.00  -2.00  -3.00  -2.00 
#  -2.00  -3.00  -2.00  -1.00 
#  -3.00  -2.00  -1.00   0.00 

在使用贪婪策略时，各状态的最终价值与均一随机策略下的最终价值不同。这体现了状态的价值是基于特定策略的。

3.4 策略迭代

编写如下代码进行贪婪策略迭代

def policy_iterate(MDP, V, Pi, n, m):
    for i in range(m):
        V = policy_evaluate(MDP, V, Pi, n)
        Pi = greedy_pi # 第一次迭代产生新的价值函数后随机使用贪婪策略
    return V

这里很多朋友就会疑惑包括我自己，一开始也疑惑上面两行赋值的意义。
实际上greedy_pi本身是个函数，其作用就是利用每次生成的V得到概率。而policy_evaluate内部则是调用了这个函数，结果生成V。

每迭代1次改善一次策略，共进行100次策略迭代：

V = [0  for _ in range(16)] # 重置状态价值
V_pi = policy_iterate(MDP, V, greedy_pi, 1, 100)
display_V(V_pi)
#   0.00  -1.00  -2.00  -3.00 
#  -1.00  -2.00  -3.00  -2.00 
#  -2.00  -3.00  -2.00  -1.00 
#  -3.00  -2.00  -1.00   0.00 

3.5 价值迭代

下面的代码展示了单纯使用价值迭代的状态价值

\[V_{k+1}(s) = \underset{a\in A}{max} [R_{s}^a + γ\sum_{s'\in S}P_{ss'}^aV_k(s')] \]

# 价值迭代得到最优状态价值过程
def compute_v_from_max_q(MDP, V, s):
    '''根据一个状态的下所有可能的行为价值中最大一个来确定当前状态价值
    '''
    S, A, R, P, gamma = MDP
    v_s = -float('inf')
    for a in A:
        qsa = compute_q(MDP, V, s, a)
        if qsa >= v_s:
            v_s = qsa
    return v_s

def update_V_without_pi(MDP, V):
    '''在不依赖策略的情况下直接通过后续状态的价值来更新状态价值
    '''
    S, _, _, _, _ = MDP
    V_prime = V.copy()
    for s in S:
        set_value(V_prime, s, compute_v_from_max_q(MDP, V_prime, s))
    return V_prime

def value_iterate(MDP, V, n):
    '''价值迭代
    '''
    for i in range(n):
        V = update_V_without_pi(MDP, V)
    return V

我们把迭代次数选择为4次，状态价值已经和最优状态价值一致了。

V = [0  for _ in range(16)] # 重置状态价值
V_star = value_iterate(MDP, V, 4)
display_V(V_star)
#   0.00  -1.00  -2.00  -3.00 
#  -1.00  -2.00  -3.00  -2.00 
#  -2.00  -3.00  -2.00  -1.00 
#  -3.00  -2.00  -1.00   0.00 

还可以编写如下的代码来观察最优状态下对应的最优策略：

def greedy_policy(MDP, V, s):
    S, A, P, R, gamma = MDP
    max_v, a_max_v = -float('inf'), []
    for a_opt in A:# 统计后续状态的最大价值以及到达到达该状态的行为（可能不止一个）
        s_prime, reward, _ = dynamics(s, a_opt)
        v_s_prime = get_value(V, s_prime)
        if v_s_prime > max_v:
            max_v = v_s_prime
            a_max_v = a_opt
        elif(v_s_prime == max_v):
            a_max_v += a_opt
    return str(a_max_v)

def display_policy(policy, MDP, V):
    S, A, P, R, gamma = MDP
    for i in range(16):
        print('{0:^6}'.format(policy(MDP, V, S[i])),end = " ")
        if (i+1) % 4 == 0:
            print("")

display_policy(greedy_policy, MDP, V_star)
#  nesw    w      w      sw   
#   n      nw    nesw    s    
#   n     nesw    es     s    
#   ne     e      e     nesw