【算法复习】动态规划

Outline

  • 动态规划原理
  • 编号动态规划：最大不下降子序列
  • 划分动态规划：矩阵链乘、凸多边形三角剖分
  • 数轴动态规划：0-1背包
  • 前缀动态规划：最长公共子序列
  • 树形动态规划：最优二分搜索树

Notes

## 动态规划原理

  • 基本思想：问题的最优解如果可以由子问题的最优解推导得到，则可以先求解子问题的最优解，在构造原问题的最优解；若子问题有较多的重复出现，则可以自底向上从最终子问题向原问题逐步求解。
  • 使用条件：可分为多个相关子问题，子问题的解被重复使用
    • Optimal substructure（优化子结构）：
      • 一个问题的优化解包含了子问题的优化解
      • 缩小子问题集合，只需那些优化问题中包含的子问题，降低实现复杂性
      • 我们可以自下而上的
    • Subteties（重叠子问题）：在问题的求解过程中，很多子问题的解将被多次使用。
  • 动态规划算法的设计步骤：
    • 分析优化解的结构
    • 递归地定义最优解的代价
    • 自底向上地计算优化解的代价保存之，并获取构造最优解的信息
    • 根据构造最优解的信息构造优化解
  • 动态规划特点：
    • 把原始问题划分成一系列子问题；
    • 求解每个子问题仅一次，并将其结果保存在一个表中，以后用到时直接存取，不重复计算，节省计算时间
    • 自底向上地计算。
    • 整体问题最优解取决于子问题的最优解（状态转移方程）（将子问题称为状态，最终状态的求解归结为其他状态的求解）

 

## 编号动态规划：最大不下降子序列

　　本类的状态是基础的基础，大部分的动态规划都要用到它，成为一个维。

  • 最长不下降子序列定义：从序列中选出若干个数组成一个新的序列，不改变他们的队伍的顺序，要求新的序列里xi≤xi+1≤xi+1.....举个例子{4,6,5,7,3}，最长不下降子序列就是{4,6,7}。

  • 子问题的表示：令dp[i]表示以第i个元素结尾的前i个元素构成的最长不下降子序列的长度
  • 优化子结构：若最长不下降子序列包括ak，则必有一个解包含a1,a2…ak-1的最长不下降子序列，dp[i]表示为前i个元素的序列的最长不下降子序列
  • 方程： dp[i] = max{dp[j] | 0<j<i , aj≥ai} + 1
  • 伪代码：

　　　　输入a[1,...,n]　　输出：最长子序列

 　　　　　

时间复杂度：O(n^2)

 

 ## 划分动态规划

【矩阵链乘】

  • 优化子结构：若计算A1~n的优化顺序在k处断开矩阵链, 即A1~n=A1~k × Ak+1~n，则在A1~n的优化顺序中，对应于子问题A1~k的解必须是A1-k的优化解，对应于子问题Ak+1~n的解必须是Ak+1~n的优化解
  • 子问题重叠性：

　　　　

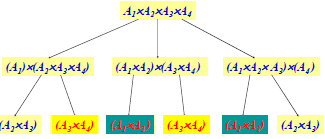
  • 方程：

假设：m[i, j] = 计算Ai~j的最小乘法数；    A1 ... AkAk+1 .... An 是优化解(k实际上是不可预知)

 　　

　    

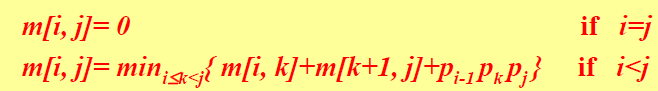
  • 伪代码：
输入：<A1, A2, ..., An>, Ai是矩阵
输出：计算A1 x A2 x ... x An的最小代价方法

Matrix-Chain-Order(p)
n=length(p)-1；
FOR i=1 TO n DO
    m[i, i]=0;
FOR l=2 TO n DO /* 计算地l对角线*/
    FOR i=1 TO n-l+1 DO
        j=i+l-1;
        m[i, j]= ∞;
        FOR k←i To j←1 DO /* 计算m[i,j] */
             q=m[i, k]+m[k+1, j]+ pi-1pkpj
             IF q<m[i, j] THEN 
                 m[i,j]=q; s[i,j]=k;
Return m and s.
Print-Optimal-Parens(s, i, j) //构建最优解，输出A1-n的优化计算顺序
 IF j=i
 THEN Print “A”i;
 ELSE Print “(”
     Print-Optimal-Parens(s, i, s[i, j])
     Print-Optimal-Parens(s, s[i, j]+1, j)
     Print “)”
  • 算法复杂度
    • 计算代价的时间：三层循环 O(n3)
    • 构建最优解的时间： O(n)
    • 总时间复杂度：O(n3)
  •  空间复杂度
    • 使用数组m和s
    • 需要空间O(n3)

 【三角剖分】

  • 优化子结构：将多边形P划分为不相交三角形的弦的集合
  • 优化问题:

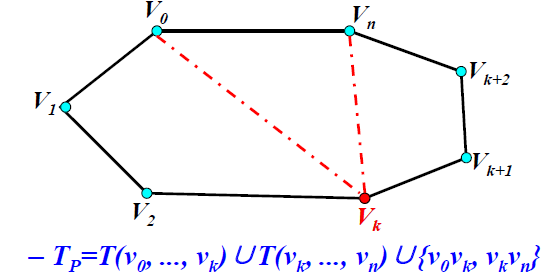
  • 方程：设t[i,j] = <vi-1,vi,.....,vj>的优化三角剖分代价

 　　

 

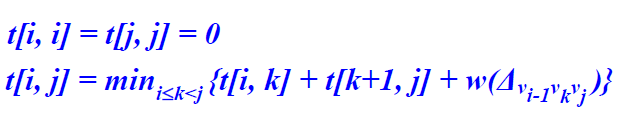
## 数轴动态规划：0-1背包

  • 问题描述：给定n种物品和一个背包，物品i的重量是wi，价值vi，背包容量为C，问如何选择装入背包的物品，使装入背包中的物品的总价值最大？对于每种物品总能选择完全装入或不装入，一个物品最多装入一次。
  • 等价整数规划问题：

　　　　

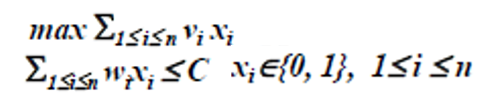
  • Naive的方法：每个物品只有两种选择：不装或装，n个物品共2n个装取方案，每个装取方案的计算代价为n，总计算代价为O(n2n)
  • 问题的划分：

 　　

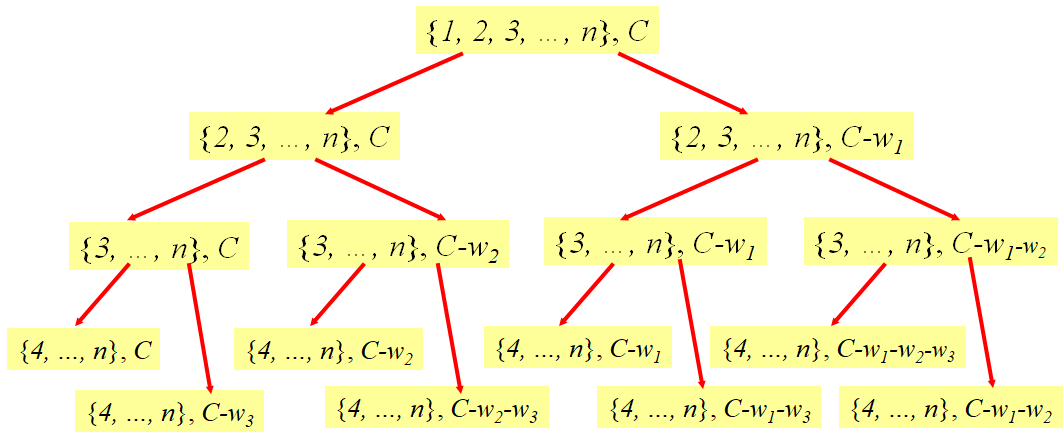
  • 定义代价矩阵m与方程：   
    • 定义m(i, j) :背包容量为j，可选物品为xi,xi+1…xn时，问题的最优解代价时m[i,j]
    • m(n, j) = 0,   0 ≤ j <wn
    • m(n, j) = vn,   j ≥wn
    • m(i, j) =  m(i+1, j), 　　      0≤ j< wi
    • m(i, j) =  max{m(i+1, j), m(i+1, j-wi)+vi},      j ≥ wi
  • 优化子结构和自底向上的代价

　　

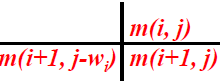
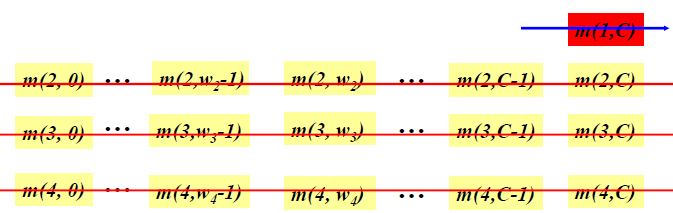
  • 伪代码

输入：C>0, wi>0, vi>0, 1≤ i≤n
输出：(x1, x2, …, xn), xi∈{0, 1}, 满足 ∑1≤i≤nwi xi ≤C, ∑1≤i≤nvi xi 最大


For j=0 To min(wn-1, C) Do
      m[n, j] = 0;
For j=wn To C Do
      m[n, j] = vn;
For i=n-1 To 2 Do
    For j=0 To min(wi -1, C)  Do
      m[i, j] = m[i+1, j];
    For j=wi  To C   Do
      m[i, j]=max{m[i+1, j], m[i+1, j-wi]+vi};
If  C<w1  Then  m[1, C]=m[2, C];
      Else  m[1, C]=max{m[2, C], m[2, C-w1]+v1};

 

m(1, C)是最优解代价值，相应解计算如下: //构造优化解
    If m(1, C) = m(2, C)
    Then x1 = 0;
    Else x1 = 1;
如果x1=0, 由m(2, C)继续构造最优解;
如果x1=1, 由m(2, C-w1)继续构造最优解.
  • 时间复杂度：
    • 计算代价的时间为O(Cn)
    • 构造最优解的时间:O(Cn)
    • 总时间复杂度为:O(Cn)
  • 空间复杂度：
    • 使用数组m，需要空间O(Cn)

 

## 前缀动态规划：最长公共子序列（LCS）

  •  问题描述：Z是序列X与Y的公共子序列如果Z是X的子序列也是Y的子序列。
  •  Naive方法：
    • 枚举X的每个子序列Z
    • 检查Z是否为Y的子序列
    • T(n)=O(n2m)
  •  优化子结构：
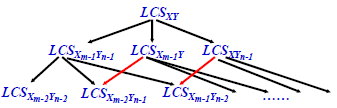
    • 设X=(x1, ..., xm)、Y=(y1, ..., yn)是两个序列， LCSXY=(z1, ..., zk)是X与Y的LCS，我们有：
    •  如果xm=yn, 则zk=xm=yn, LCSXY = LCSXm-1Yn-1 + <xm=yn>,   LCSXm-1Yn-1是Xm-1和Yn-1的LCS.
    •  如果xm≠yn，且zk≠xm，则LCSXY是Xm-1和Y的LCS，即 LCSXY = LCSXm-1Y
    •  如果xm≠yn,且zk≠yn,则LCSXY是X与Yn-1的LCS，即 LCSXY = LCSXYn-1

　　　　

  • 子问题重叠性

  • 方程：

　　　　

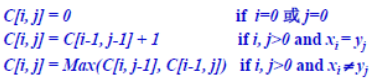
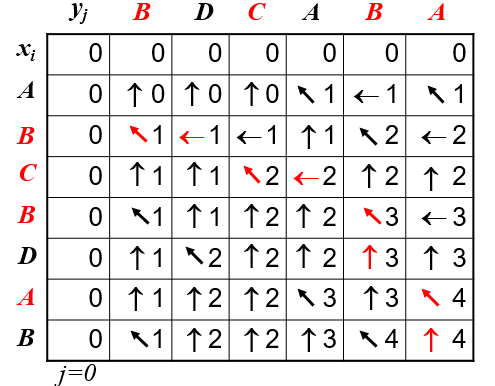
  •  自底向上计算：

　　　　

  • 伪代码

输入：X = (x1,x2,...,xm)，Y = (y1,y2,...yn)
输出：Z = X与Y的最长公共子序列

C[0:m,0:n]: C[i,j]是Xi与Yj的LCS的长度   B[1:m,1:n]:
B[i,j]是指针，指向计算C[i,j]时所选择的子问题的优化解所对应的C表的表项

LCS-length(X, Y)
m←length(X)；n←length(Y)；
For i←0 To m Do C[i,0]←0;
For j←0 To n Do C[0,j]←0;
For i←1 To m Do
  For j←1 To n Do
    If xi = yj
    Then C[i,j]←C[i-1,j-1]+1；B[i,j]←“↖”;
      Else If C[i-1,j]≥C[i,j-1] Then
              C[i,j]←C[i-1,j]; B[i,j]←“↑”;
           Else C[i,j]←C[i,j-1]; B[i,j]←“←”;
Return C and B.

Print-LCS(B, X, i, j)
IF i=0 or j=0 THEN Return;
IF B[i, j]=“↖”
THEN Print-LCS(B, X, i-1, j-1);
    Print xi;
ELSE If B[i, j]=“↑”
    THEN Print-LCS(B, X, i-1, j);
    ELSE Print-LCS(B, X, i, j-1).

Print-LCS(B, X, length(X), length(Y))
      可打印出X与Y的LCS。
  • 时间复杂度：
    • 计算代价的时间：O(mn)
    • 构造最优解的时间：O(m+n)
    • 总时间复杂度为： O(mn)
  • 空间复杂度：
    • 使用数组C和B，需要空间O(mn)

 

## 树形动态规划

 

 

posted @ 2018-06-26 16:41  HongmingYou  阅读(110717)  评论(0)  编辑  收藏  举报