【算法复习】分治算法
Outline
- 分治思想和递归表达式
- 大整数乘法
- 矩阵乘法的Strassen算法
- 快速傅里叶变化
- 基于分治的排序
- merge-sort排序
- 快速排序
- 排序的下界问题
- 中位数和顺序统计量
- 最邻近点对
- 凸包
Notes
## 分治思想和递归表达式
【分治思想】
将一个问题分解为与原问题相似但规模更小的若干子问题,递归地解这些子问题,然后将这些子问题的解结合起来构成原问题的解。这种方法在每层递归上均包括三个步骤:
- divide(分解):将问题划分为若干个子问题
- conquer(求解):递归地解这些子问题;若子问题Size足够小,则直接解决之
- Combine(组合):将子问题的解组合成原问题的解
【分治递归表达式】
- 设T(n)是Size为n的执行时间,若Size足够小,如n ≤ C (常数),则直接求解的时间为θ(1)
- ①设完成划分的时间为D(n)
- ②设分解时,划分为a个子问题,每个子问题为原问题的1/b,则解各子问题的时间为aT(n/b)
- ③设组合时间C(n)
- 则有递归方程总结为:
- T(n)=θ(1) if n<c
- T(n)=aT(n/b)+D(n)+C(n) if n≥c
- 技术细节(注意):
- 在声明、求解递归式时,常常忽略向上取整、向下取整、边界条件
- 边界条件可忽略,这些细节一般只影响常数因子的大小,不改变量级。求解时,先忽略细节,然后再决定其是否重要!
## 大整数乘法
*********优化划分阶段,降低 T(n)=aT(n/b) + f(n) 中的 a*********
这里我们假设有两个大整数X、Y,分别设X=1234、Y=5678。现在要求X*Y的乘积,小学的算法就是把X与Y中的每一项去乘,但是这样的乘法所需的时间复杂度为O(n^2),效率低下,我们可以尝试使用分治来解决。

XY = (A2n/2 + B)(C2n/2 + D)
= AC2n + (AD+BC)2n/2 + BD
= AC2n + ((A-B)(D-C)+AC+BD)2n/2 + BD
- 算法分析:
- 首先将X和Y分成A,B,C,D
- 此时将X和Y的乘积转化为上述式子,把问题转化为求解式子的值
- 此时递归式为 T(n)=4T(n/2)+θ(n)
- 算法复杂度 T(n)=θ(n2)
- 继续优化: AD+BC=(B-A)(C-D)+AC+BD
- 算法过程:
- 划分产生A,B,C,D;
- 计算 B-A 和 C-D;
- 计算 n/2 位乘法 AC、BD、(B-A)(C-D);
- 计算 (B-A)(C-D) + AC + BD;
- AC左移n位,((B-A)(C-D) + AC + BD) 左移n/2位;
- 计算XY
- 递推式:
- T(n)=θ(1) if n=1
- T(n)=3T(n/2)+O(n) if n>1
- 算法复杂度: T(n)=O(nlog3) =O(n1.59)
## 矩阵乘法的Strassen算法
【矩阵相乘的朴素算法 T(n) = Θ(n3)】
朴素矩阵相乘算法,思想明了,编程实现简单。时间复杂度是Θ(n^3)。伪码如下
1 for i ← 1 to n 2 do for j ← 1 to n 3 do c[i][j] ← 0 4 for k ← 1 to n 5 do c[i][j] ← c[i][j] + a[i][k]⋅ b[k][j]
【矩阵相乘的strassen算法 T(n)=Θ(nlog7) =Θ (n2.81)】

一般算法需要八次乘法,四次加法;算法效率是Θ(n^3);
鉴于上面的分治法方案无法有效提高算法的效率,要想提高算法效率,由主定理方法可知必须想办法将2中递归式中的系数8减少。Strassen提出了一种将系数减少到7的分治法方案,如下图所示。

我们可以看到上面只有7次乘法和多次加减法,最终达到降低复杂度为O( nlg7 ) ~= O( n2.81 );

SQUARE-MATRIX-MULTIPLY-RECURSIVE(A,B) n=A.rows let C be a new n*n matrix if n==1 c11=a11*b11 else partition A, B and C as in equation(1) C11=SQUARE-MATRIX-MULTIPLY-RECURSIVE(A11,B11) + SQUARE-MATRIX-MULTIPLY-RECURSIVE(A12,B21) C22=SQUARE-MATRIX-MULTIPLY-RECURSIVE(A11,B12) + SQUARE-MATRIX-MULTIPLY-RECURSIVE(A12,B22) C21=SQUARE-MATRIX-MULTIPLY-RECURSIVE(A21,B11) + SQUARE-MATRIX-MULTIPLY-RECURSIVE(A22,B21) C22=SQUARE-MATRIX-MULTIPLY-RECURSIVE(A21,B22) + SQUARE-MATRIX-MULTIPLY-RECURSIVE(A22,B22) return C
## 快速傅里叶变换(FFT)
问题定义:

算法思想:


伪代码:

递归方程:
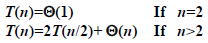
算法复杂度: T(n) = θ(n logn)
## 基于分治的排序
【归并排序】
归并排序是分治思想的典型应用,
划分策略:根据中间点将数组集合划分成两部分,不断递归
合并策略:比较a[i]和b[j]的大小,若a[i]≤b[j],则将第一个有序表中的元素a[i]复制到r[k]中,并令i和k分别加上1;否则将第二个有序表中的元素b[j]复制到r[k]中,并令j和k分别加上1,如此循环下去,直到其中一个有序表取完,然后再将另一个有序表中剩余的元素复制到r中从下标k到下标t的单元。
MergeSort(A,i,j) Input: A[i,…,j] Output:排序后的A[i,…,j] 1. k ← (i+j)/2; 2. MergeSort(A,i,k); 3. MergeSort(A,k+1,j); 4. l←i; h ← k+1; t=i; //设置指针 5. While l≤k & h< j Do 6. IF A[l] < A[h] THEN B[t] ← A[l]; l ← l+1; t ← t+1; 7. ELSE B[t] ← A[h]; h ← h+1; t ← t+1; 8. IF l<k THEH //第一个子问题有剩余元素 9. For v ← l To k Do 10. B[t] ← A[v]; t ← t+1; 11. IF h<j THEN //第二个子问题有剩余元素 12. For v ← h To j Do 13. B[t] ← A[v]; t ← t+1; 14. For v ← i To j Do //将归并后的数据复制到A中 15. A[v] ← B[v];
复杂度分析: T(n)=2T(n/2)+O(n) T(n)=O(nlogn)
复习:归并排序具有如下特点:
- 归并排序的时间复杂度为O(nlogn),这是基于比较的排序算法所能达到的最高境界;
- 归并排序是一种稳定的算法,这一点在某些场景下至关重要;
- 归并排序是最常用的外部排序方法(当待排序的记录放在外存上,内存装不下全部数据时,归并排序仍然适用,当然归并排序同样适用于内部排序...);
- 但其也需要O(n)的辅助空间,而与之效率相同的快排和堆排分别需要O(logn)和O(1)的辅助空间,在同类算法中归并排序的空间复杂度略高
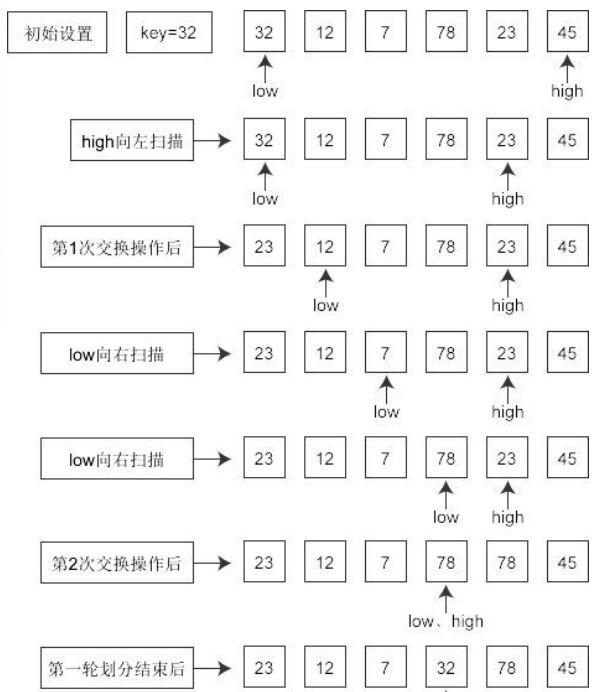
【快速排序】
划分策略:选取一个记录作为枢轴,经过一趟排序,将整段序列分为两个部分,其中一部分的值都小于枢轴,另一部分都大于枢轴。
递归策略:然后继续对这两部分继续进行排序,从而使整个序列达到有序。
合并策略:无操作
QuickSort(A,i,j) Input: A[i,…,j], x Output: 排序后的A[i,…,j] 1. temp←rand(i,j); //产生i,j之间的随机数 2. x ← A[temp]; //以确定的策略选择x 3. k=partition(A,i,j,x); //用x完成划分 4. QuickSort(A,i,k); //递归求解子问题 5. QuickSort(A,k+1,j);
Partition(A,i,j,x)
1. low←i ; high ←j;
2. While( low< high ) Do
3. swap(A[low], A[high]);
4. While( A[low] < x ) Do
5. low←low+1;
6. While( A[low] < x ) Do
7. high←high-1;
8. return(high)
平均、最优的时间复杂度为O(nlogn),最差的时间复杂度为O(n^2)
平均的空间复杂度为O(logn),最差的空间复杂度为O(n)
排序的下界是:Ω(n log n)
## 中位数和顺序统计量
【最大值最小值】
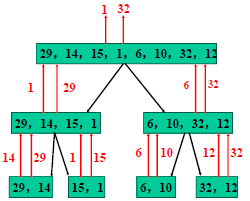
算法MaxMin(A) 输入: 数组A[i,…,j] 输出:数组A[i,…,j]中的max和min 1. If j-i+1 =1 Then 输出A[i],A[i],算法结束 2. If j-i+1 =2 Then 3. If A[i]< A[j] Then输出A[i],A[j];算法结束 4. k←(j-i+1)/2 5. m1,M1 ←MaxMin(A[i:k]); 6. m2,M2 ←MaxMin(A[k+1:j]); 7. m ←min(m1,m2); 8. M ←max(M1,M2); 9. 输出m,M
时间复杂度分析:T(n) = 3n/2 - 2
所以时间复杂度为:O( ⌊3n/2⌋ )
【中位数的线性时间选择算法】
- 这种算法在最坏的情况下的时间复杂度为O(n),其具体过程如下:
- 将输入数组划分为n/5组,每组有5个元素,且剩下的至多有一组的元素小于5个。
- 寻找这n/5个组中每个组的中位数,可以将每组做一次排序,然后选取每组的第三个元素。
- 对于第2部找出的n/5个中位数递归的调用Select函数求出其中位数x.(约定偶数个中位数为其较小的中位数)
- 按照找到的中位数x将数组划分为两个部分,求得小于或者等于x的元素有q个
- 如果k==q则返回x,若k<q则在x的左区间找第k小的数,否则在x的有区间找第k-q大的数
Input: 数组A[1:n], 1≤i≤n Output: A[1:n]中的第i-大的数 1. for j←1 to n/5 2. InsertSort(A[(j-1)*5+1 : (j-1)*5+5]); 3. swap(A[j], A[[(j-1)*5+3]); 4. x ←Select(A[1: n/5], n/10 ); 5. k ←partition(A[1:n], x); 6. if k=i then return x; 7. else if k>i then retrun Select(A[1:k-1],i); 8. else retrun Select(A[k+1:n],i-k);
递归方程式:T(n) ≤ T( ⌈n/5⌉ ) +T(7n/10+6) + O(n)
时间复杂度:T(n) = O(n)
## 最邻近点对
- 输入:Euclidean空间上的n个点的集合Q
- 输出:P1, P2∈Q, Dis(P1, P2)=Min{Dis(X, Y) | X, Y∈Q}
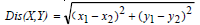
- 算法过程:
- 如果Q中仅包含一个点,则算法结束;
- 把Q中点分别按x-坐标值和y-坐标值排序.
- 划分:
- 计算Q中各点x-坐标的中位数m;
- 用垂线 L:x=m 把Q划分成两个大小相等的子集合QL 和QR, QL中点在L左边, QR 中点在L右边.
- 求解:
- 递归地在QL、QR中找出最接近点对:(p1, p2)∈QL , (q1, q2)∈QR
- d=min{Dis(p1, p2), Dis(q1, q2)};
- 合并:
- 在临界区查找距离小于d的点对(pl, qr), pl∈QL,qr∈QR;
- 如果找到,则(pl, qr)是Q中最接近点对,否则(p1, p2)和(q1, q2) 中距离最小者为Q中最接近点对
- 时间复杂度:
- Divide阶段需要O(n)时间
- Conquer阶段需要2T(n/2)时间
- Merge阶段需要O(n)时间
- 递归方程
- T(n)= O(1) n = 2
- T(n) = 2T(n/2) + O(n) n ≥ 3
- 用Master定理求解T(n)
- T(n) = O(nlogn)

## 凸包



