【论文阅读】大模型参数高效微调方式——LORA

本文成文于23年5月，当时的市场热点正在从“超大模型训练到微调应用”转变。

一段话总结：面向大模型的全参数finetune 需要很高的计算消耗和存储成本，学界开始探索参数高效的微调方法。LoRA就是其中的代表，他在原始的Transformer模型上插入少量的参数，只训练增量的参数就能达到与全参数finetune相同/更优的效果。
原文：https://arxiv.org/pdf/2106.09685.pdf

一、Motivation

Full Finetune的本质： \(W \rightarrow W + \Delta W\) ，其中\(\Delta W=\alpha\cdot\left(-\nabla L_W\right)\) 通过反向传播求得

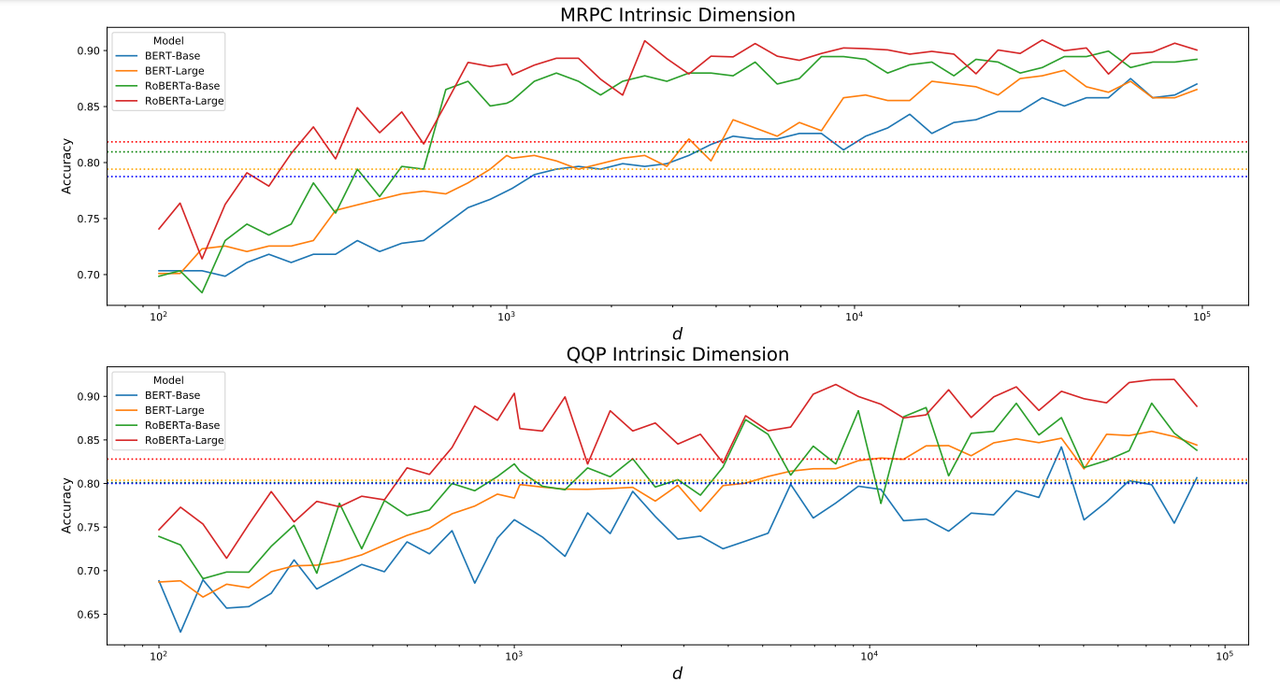
• 前序工作发现大模型微调时 \(\Delta W\) 是欠秩的 [ACL2021 Meta]，即使用很低的参数维度就能达到全量finetune 90%的水平。
• 从另一个角度理解，虽然语言模型整体参数空间很大，但具体到每个任务其实有各自的隐表征空间(intrisic dimension)，这个隐表征的维度并不高。对于每个下游任务、只在低维的空间内学习就ok。
  

二、Methods

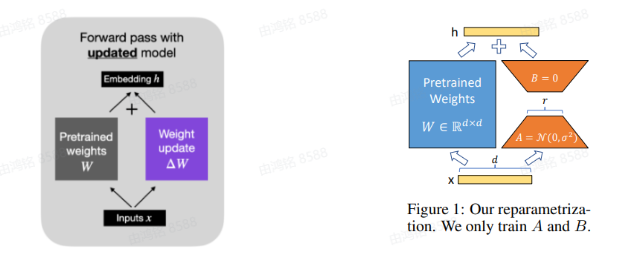
方法： \(\Delta W_{d \times h}\) 做低秩分解，分解为 \(B A,  B \in \mathbb{R}^{d \times r}, A \in \mathbb{R}^{r \times k}\)，其中 \(r\ll{min\{d,k\}}\)。

• 在训练过程中，模型主体的参数freeze、只训Lora的部分。在推理的时候pretrain和lora部分一起用。
  

• 可训练参数从 \(d \times h\) 降至\(d\times{r}+h\times{r}\)。训练消耗的显存从 \(16\Phi\) bytes 降低至 \((4 \Phi+16 \Theta)\) bytes，有效降低显存诉求。

  • 其中，\(\Phi\)是全部可训练参数，\(\Theta\)是Lora方法下的可训练参数。在GPT-2的案例中，\(\Theta \approx 0.1\% \Phi\)
  • 每一个可训练参数在混合精度训练的情况下，需要2byte存parameter、2bytes存grad、12bytes存optimizer states，详见 ZeRO文章

• 理论如此，现实有很多细节问题：Lora 模型中的哪些参数？ \(r\)如何选取？ 这么做真的有效么？

三、Analyse

问题一：Lora 模型中的哪些参数

• 结论：只微调 self-attention模块的参数、不微调MLP的参数；
• 背景知识：自注意力模块内置四个参数矩阵
  
• 实验：控制可调节的参数总量，消融实验看怎么配置效果最好，四个参数都调的效果最好、只微调 \(W_q和W_v\)的效果也ok。
  

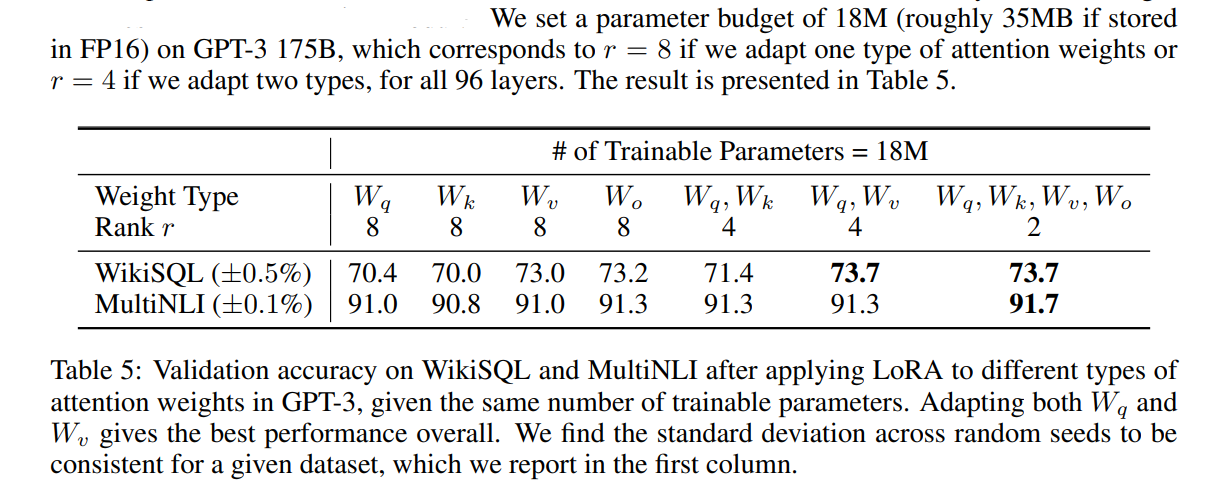
问题二：\(\Delta W\) 真的是欠秩的么，r 要怎么选

• 结论： r设置一个很小的值就能达到满秩训练的效果；且从数学的角度分析 \(A_{r=8} 与 A_{r=64}\)非常相似
• 实验： r取4~8时就能得到很好地效果
  
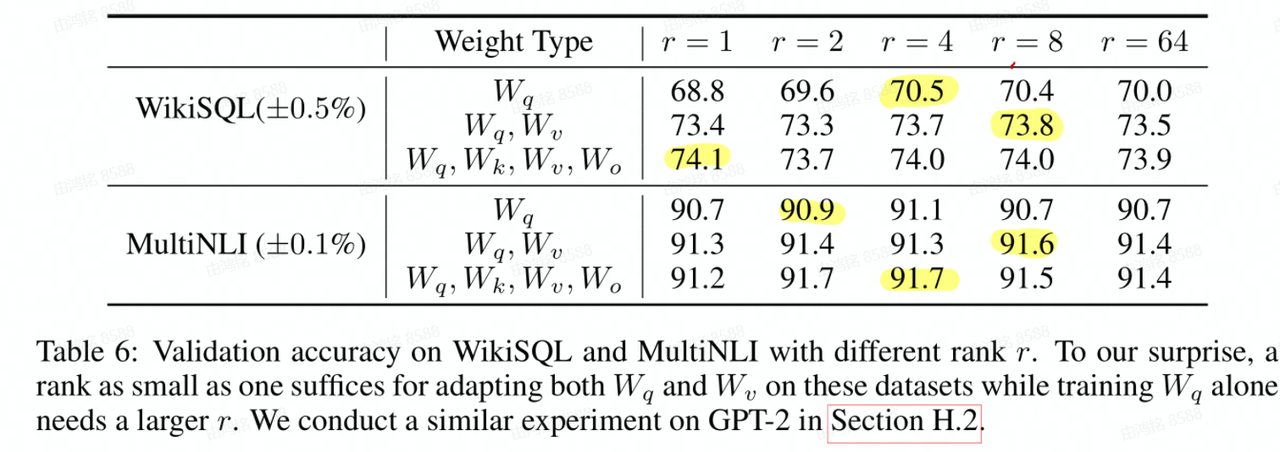
• 分析：对 r=8 和 r=64 时获得的 \(\Delta W\)进行奇异值分解，发现 高奇异值对应的奇异向量的相似度很高 ( >0.5)、证明两个\(\Delta W\)子空间的相似性很高。
  

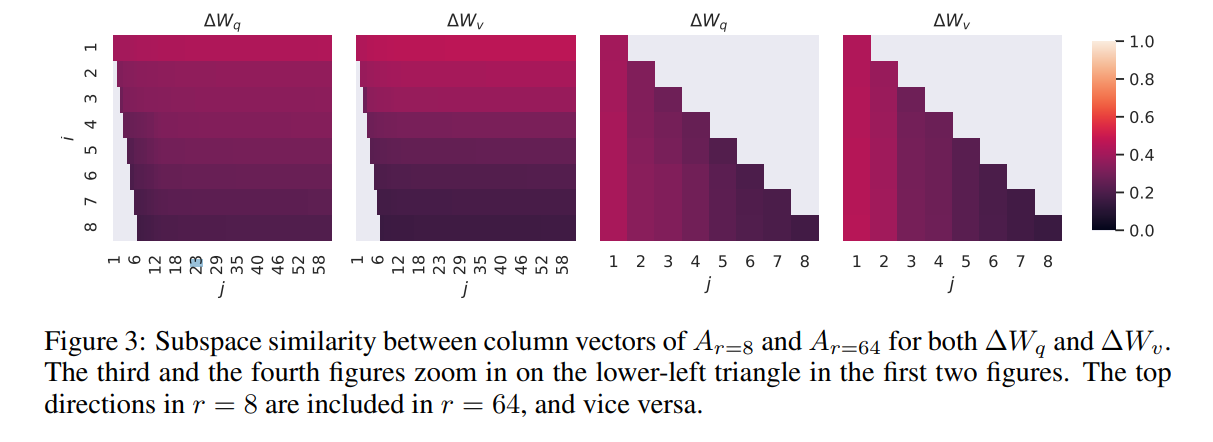
问题三：这么做真的有效么、\(\Delta W\) 到底学了啥

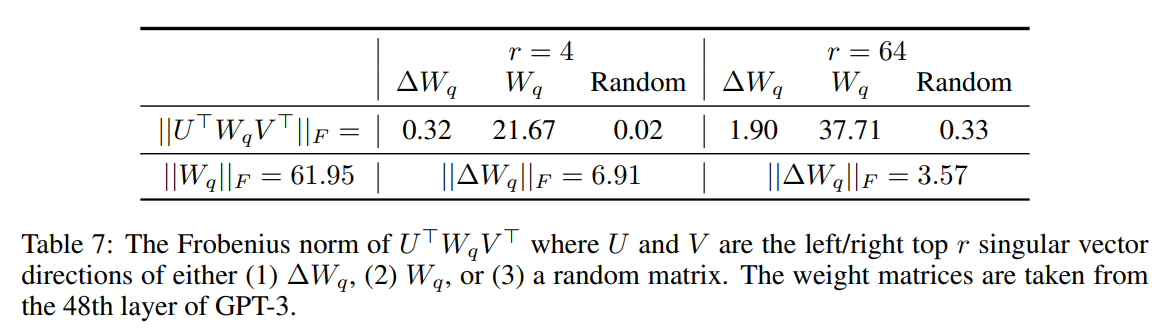
• 结论：\(\Delta W\) 跟预训练参数\(W\)有更强的相关性，它强化了 $$W$$当中原有的非重点特征，这些特征是下游任务更需要的。
• 分析：思路是把 \(W\) 投影到 \(\Delta W\)的空间内计算F范数(衡量空间内的相关度)，原始参数0.32、微调参数6.91，加强了其中的部分特性。
  

四、Performance

五、Practice

output_dim = 768  # e.g., the output size of the layer
rank = 8  # The rank 'r' for the low-rank adaptation

W = ... # from pretrained network with shape input_dim x output_dim

W_A = nn.Parameter(torch.empty(input_dim, rank)) # LoRA weight A
W_B = nn.Parameter(torch.empty(rank, output_dim)) # LoRA weight B

# Initialization of LoRA weights
nn.init.kaiming_uniform_(W_A, a=math.sqrt(5))
nn.init.zeros_(W_B)

def regular_forward_matmul(x, W):
    h = x @ W
return h

def lora_forward_matmul(x, W, W_A, W_B):
    h = x @ W  # regular matrix multiplication
    h += x @ (W_A @ W_B)*alpha # use scaled LoRA weights
return h```