偏差-方差分解

 

最近在看机器学习周志华那本书，受益颇多。我们先抛过来几个问题，再一一解答。

• 什么是偏差-方差分解？为什么提出这个概念？

• 什么是偏差？什么是方差？

• 什么是偏差-方差窘境？应对措施？

1、偏差-方差分解的提出

我们知道训练往往是为了得到泛化性能好的模型，前提假设是训练数据集是实际数据的无偏采样估计。但实际上这个假设一般不成立，针对这种情况我们会使用训练集训练，测试集测试其性能，上篇博文有介绍评估策略。对于模型估计出泛化性能，我们还希望了解它为什么具有这样的性能。这里所说的偏差-方差分解就是一种解释模型泛化性能的一种工具。它是对模型的期望泛化错误率进行拆解。

2、偏差-方差分解推导

样本可能出现噪声，使得收集到的数据样本中的有的类别与实际真实类别不相符。对测试样本 x，另 y_d 为 x 在数据集中的标记，y 为真实标记，f(x;D) 为训练集D上学得模型 f 在 x 上的预测输出。接下来以回归任务为例：

模型的期望预测：

 

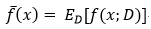
样本数相同的不同训练集产生的方差：

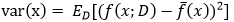
噪声：

期望输出与真实标记的差别称为偏差：

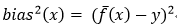
 为便于讨论，假设噪声期望为0，即：E_D[y-y_D]=0，通过简单的多项式展开与合并，模型期望泛化误差分解如下：

画红线部分是分解后由这三部分方差、偏差、噪声组成。偏差那部分因为和D无关，所以去掉了E_D。画蓝线部分用了数学技巧，并且有两项等于0约简。

3、偏差、方差、噪声

偏差：度量了模型的期望预测和真实结果的偏离程度，刻画了模型本身的拟合能力。

方差：度量了同样大小的训练集的变动所导致的学习性能的变化，即刻画了数据扰动所造成的影响。

噪声：表达了当前任务上任何模型所能达到的期望泛化误差的下界，刻画了学习问题本身的难度。

4、偏差-方差窘境

为了得到泛化性能好的模型，我们需要使偏差较小，即能充分拟合数据，并且使方差小，使数据扰动产生的影响小。一般来讲，偏差和方差在一定程度上是有冲突的，这称作为偏差-方差窘境。

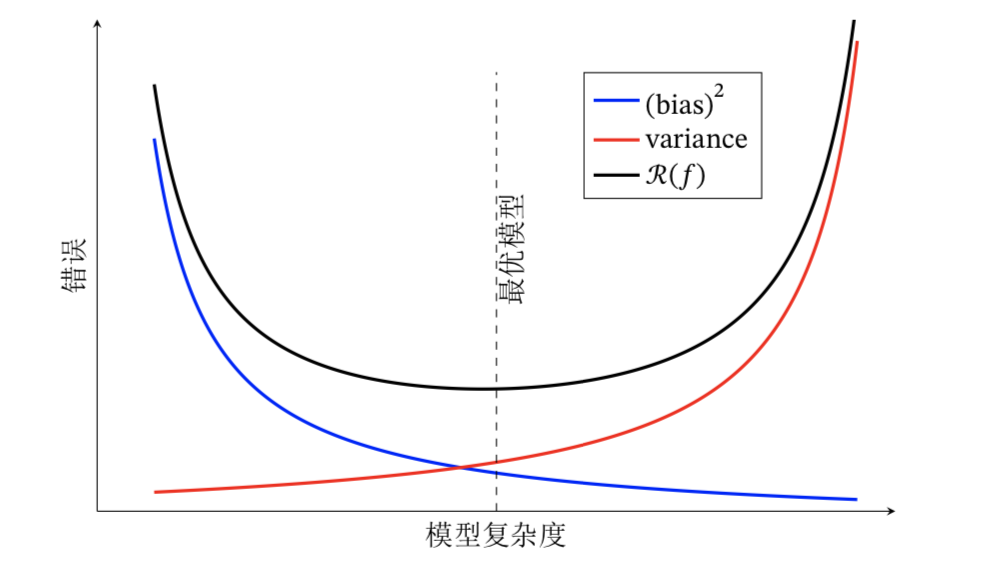
下图中的R(f)是指泛化误差，图中展现了方差、偏差和泛化误差之间的关系。在模型训练不足时，拟合能力不够强，训练数据的扰动不足以使学习器产生显著变化，此时偏差主导泛化误差，此时称为欠拟合现象。当随着训练程度加深，模型的拟合能力增强，训练数据的扰动慢慢使得方差主导泛化误差。当训练充足时，模型的拟合能力非常强，数据轻微变化都能导致模型发生变化，如果过分学习训练数据的特点，则会发生过拟合。

针对欠拟合，我们提出集成学习的概念并且对于模型可以控制训练程度，比如神经网络加多隐层，或者决策树增加树深。针对过拟合，我们需要降低模型的复杂度，提出了正则化惩罚项。