机器学习-类别不平衡问题
-
引言：我们假设有这种情况，训练数据有反例998个，正例2个，模型是一个永远将新样本预测为反例的学习器，就能达到99.8%的精度，这样显然是不合理的。
-
类别不平衡：分类任务中不同类别的训练样例数差别很大。
一般我们在训练模型时，基于样本分布均匀的假设。从线性分类器的角度讨论，使用 y=wTx+b 对新样本分类时，用预测的 y 与一个阈值进行比较，y>0.5 即判别为正例，否则判别为负例。这里的 y 实际表达了正例的可能性（1-y是反例的可能性），0.5表明分类器认为正反例可能性相同。即
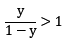，则预测为正例
但如果训练集中正反例数目相差悬殊，另m+表示正例数目，m-表示反例数目，则在大数的基础上，观测几率就代表了真实几率，只要分类器的预测几率高于观测几率就判定为正例，即
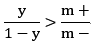，预测为正例
我们知道分类器是基于上一个公式决策的，则稍加调整
也就是 y > m+/(m++m-) 即判定为正例，实际上想想也很简单，本来是假设正负例各占一半，所以是0.5，现在类别样本数目不均衡，所以需要大于实际正例数目所占比。以上就是类别不平衡学习的一个基本策略——“再缩放”。实际上，这种策略也是一种代价敏感学习，将 m-/ m+ 用 cost+/cost- 代替，其中cost+ 是将正例误分为反例的代价，cost-相反。
实际上，再缩放实际操作起来不现实，因为假设的前提训练集是真实的样本总体的无偏采样往往不成立，所以观测几率未必有效。另外两种比较常用的解决方案如下：
1、欠采样
对训练集里的反例样本进行“欠采样”，即去除一些反例使得正反例数目接近，再进行学习。由于丢弃很多反例，会使得训练集远小于初始训练集，所以有可能导致欠拟合。所以提出以下策略
代表算法：EasyEnsemble
利用集成学习机制，每次从大多数类中抽取和少数类数目差不多的重新组合，总共构成n个新的训练集，基于每个训练集训练出一个AdaBoost分类器（带阈值），最后结合之前训练分类器结果加权求和减去阈值确定最终分类类别。
2、过采样
增加一些正例使得正反例数目接近，然后再学习。需要注意的是不能只是对初始正例样本重复采样，否则导致严重的过拟合。所以提出以下策略
代表算法：SMOTE
合成新的少数样本的策略是，对每个少类a样本，从最近邻中随机选一个样本b，在a、b之间连线上随机选一点作为合成新样本。
基于算法的改进：SMOTE可能导致初始样本分布有的部分更加稠密，有的部分更加稀疏，而且使得正反例的边界模糊。所以有学者提出 Borderline-SMOTE算法，将少数类样本根据距离多数类样本的距离分为noise,safe,danger三类样本集，只对danger中的样本集合使用SMOTE算法。
