机器学习之PCA(1)
• 连续潜变量模型
• 经常有一些数据的未知的潜在的原因。
• 到目前为止,我们已经看了模型与离散的潜变量,如混合高斯模型的。
• 有时,依照我们观察到的数据是由连续因素控制的去思考更合适。
• 动机:对于许多数据集,数据点处于接近比原来的数据空间维数低得多的复本(manifold)。
• 训练连续潜变量模型通常被称为降维,因为通常有许多更少的潜在维度。
• 例子:主成分分析、因子分析、独立成分分析。
内在的潜在维度
•这两个数据中的内在潜在维度是什么

• 我们如何从高维数据中找到这些潜在的维度。
人类是生活在三维空间里的动物,但是照片是二维的。
内在的潜在维度
• 在这个数据集,只有3自由度的可变性——垂直和水平对应翻译,和旋转。

每个图像进行随机位移和旋转在一些更大的图像。
结果图像100*100 = 10000像素。
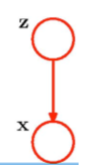
产生式观点:
• 每个数据示例生成都来自于先选择在一个在隐空间中的分布的一个点,然后从输入空间的条件分布中生成一个点
*.最简单潜变量模型:假设潜变量和观测变量均为高斯分布。
*这导致概率公式的主成分分析和因子分析。
*我们首先看看标准主成分分析,然后考虑它的概率的形成。
• 概率公式的优点:使用EM进行参数估计, PCAs(主成分分析技术)的混合、贝叶斯PCA。
PCA(主成分分析:Principal Component Analysis )
用途: 用于数据压缩、可视化、特征提取,降维。
• 目标是在D维数据中找到潜在的M主成分——
选择S的(数据协方差矩阵)M个最高(top)特征向量:{u1,u2,……,um};
也就是选择其中比较具有代表性的特征组成一个向量。
投射每个输入向量x到这个子空间,比如: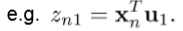
ui={xu1,xu2,xu3……,xun} 1*n维,
数据的特征有M个,数据有N个,这样{u1,u2,……,um}是N*M维,
完整投影成M维需要的形式:
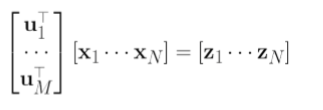
两个视角/派生:

最大化方差(绿点的散射)。
最小化错误(每个数据点红绿距离)。
最大方差公式
考虑数据集{ x1,…,xN },xN 属于R( )。
)。
我们的目标是把数据投射到一个M维空间(M维<D维)
• 考虑投影到M = 1维空间。
用d维单位向量u1定义这个空间的方向,所以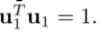
目的:最大化投影数据相对于u1的方差(这意味着包含更多的信息)
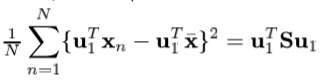
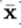 是样本均值(期望),
是样本均值(期望),
S是数据协方差矩阵。
N是样本数量。
u1第一个特征
用整个样本去最大化特征U1.


其中样本均值和数据协方差为:
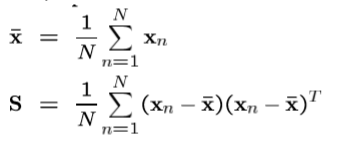





 浙公网安备 33010602011771号
浙公网安备 33010602011771号