数学知识：Convex Optimization A

目录

• 1. Introduction
  • mathmetical optimization
  • examples
  • solving optimization problems
  • least-squares
  • linear programming problem
  • convex optimization problem
  • example
  • course goals and topics
  • nonlinear optimization
• 2. Convex sets
  • affine set
  • convex set
  • convex combination and convex hull
  • convex cone
  • hyperplane and half-sapces
  • euclidean balls and ellipsoids
  • norm balls and cones
  • polyhedra
  • positive semidefinite cone
  • operations that preserve convexity
  • intersection
  • affine function
  • perspective and linear-fractional function
  • generalized inequalities
  • minimum and minimal elements
  • separating hyperplane thoerem
  • supporting hyperplane theorem
  • dual cones and generalized inequalities
  • minimum and minimal elements via dual inequality
• Convex functions
  • definition
  • examples on \(\mathbf{R}\)
  • example on \(\mathbf{R}^n\) and \(\mathbf{R}^{m\times n}\)
  • restriction of a convex function to a line
  • extended-value extension
  • first-order condition
  • second-order condition
  • examples
  • epigraph and sublevel set
  • Jense's inequality
  • operations that preserve convexity
  • positive weighted sum & composition with affine function
  • pointwise maximum
  • pointwise supremum
  • composition with scalar functions
  • vector composition
  • minimization
  • perspective
  • the conjugate function
  • quasiconvex functions
  • examples
  • properties
  • log-concave and log-convex functions
  • properties of log-concave functions
  • consequences of integration property
  • convexity with respect to generalized inequalities

1. Introduction

• mathematical optimization
• least-squares and linear programing
• convex optimization
• example
• course goals and topics
• nonlinear optimization
• brief history of convex optimization

mathmetical optimization

optimization problem

\[minimize~~f_0(x) \]

\[subject~to~~f_i(x){\leq}b_i,i=1,...,m \]

• \(x=(x_1,...,x_n)\): optization variables
• \(f_0:R^n{\rightarrow}R\): objective function
• \(f_i:R^n{\rightarrow}R,~i=1,...,m\): constraint functions

optimal solution \(x^*\) has smallest value of \(f_0\) among all vectors that satisfy the constraints

examples

portfolio optimization

• variables:amounts inveated in different assets
• constraints:budget,max./min. investment per asset, minimum return
• objective:overall risk or return variance

device sizing in eletronic circuits

• variables: device widths and lengths
• constraints: manufacturing limits, timing requirements, maximum area
• objective: power consumption

data fiting

• variables: model parameters
• constraints: prior information, parameter limits
• objective: measure of misfit or prediction error

solving optimization problems

general optimization problem

• very difficult to solve
• methods involve some compromise, e.g., very long computation time or not always finding the solution

examples: certain problem classes can be solved efficiently and reliably

• least-squares problems
• linaer programming problems
• convex optimization problems

least-squares

\[minimum~~{\parallel}Ax-b{\parallel}_2^2 \]

solving least-square problems

• analytical solution: \(x^*=(A^TA)^{-1}A^Tb\)
• reliabe and efficient algorithems and software
• computation time proportional to \(n^2k(A{\in}R^{k×n})\); less if structured
• a mature technology

using least-squares

• least-squares problems are easy to recognize
• a few standard techniques increase flexibility(e.g., including weights, adding regularization terms)

linear programming problem

\[minimize~~c^Tx \]

\[subject~to~~a_i^Tx{\le}b_i,~i=1,...,m \]

solving linear programs

• no analytical formula for solution
• reliable and efficient algorithms and software
• computation time proportional to \(n^2m\) if \(m{\ge}n\); less with structure
• a mature technology

using linaer programming

• not as easy as least-square problems
• a few standard tricks used to convert problems to linear programs(e.g., problems involving \(l_1\) or \(l_{\infty}\) norms, piecewise-linear functions)

convex optimization problem

\[minimum~~f_0(x) \]

\[subject~to~f_i(x){\le}b_i,i=1,...,m \]

• objective and constraint are convex:

\[f_i({\alpha}x+{\beta}y){\le}{\alpha}f_i(x)+{\beta}f_i(y) \]

if \({\alpha}+{\beta}=1, {\alpha}{\ge}0, {\beta}{\ge}0\)

• includes least-square problems and linaer program problems as special cases

solving convex optimization problem

• no analytic solution
• reliable and efficient algorithms
• consumption time proportional to \(max\{n^3, n^2m, nm^2, F\}\), where \(F\) is cost of evaluating \(f_i\)'s and their first and second derivatives
• almost a technology

using convex optimization

• often difficult to recognize
• many triks for transforming problems into convex form
• surprisingly many problems can be solved via convex optimization

example

\(m\) lamps illuminating \(n\)(small, flat) patches
intensity \(I_k\) at patch \(k\) depends linearly on lamp power \(p_j\):

\[I_k=\sum\limits_{j=1}^m a_{kj} p_j,~~~~~~~a_{kj}=r_{kj}^{-2}max\{cos\theta_{kj},0\} \]

problem: achieve desired illumination \(I_{des}\) with bounded lamp powers

\[minimium~\mathop{max}\limits_{k=1,...,n}~\lvert logI_k-logI_{des}\rvert \]

\[subject~to~~0 \le p_j \le p_{max},~j=1,...,m \]

solution

1. use uniform power: \(p_j=p\), vary \(p\)
2. use least-squares:

\[minimum~~\sum\limits_{k=1}^n(I_k-I_{des})^2 \]

round \(p_j\) if \(p_j>p_max\) or \(p_j<0\)

3. use weighted least-squares:

\[minimize~\sum\limits_{k=1}^n(I_k-I_{des})^2+\sum\limits_{j=1}^m w_j (p_j-p_{max}/2)^2 \]

iteratively adjust weights \(w_j\) until \(0 \le p_j \le p_{max}\)

1. use linear programming:

\[minimium~~\mathop{max}\limits_{k=1,...,n}~\lvert I_k-I_{des}\rvert \]

\[subject~to~~0 \le p_j \le p_{max}, ~j=1,...,m \]

which can be solved via linear programming

1. use convex optimization: problem is equivalent to

\[minimum~~f_0(p) =\max\limits_{k=1,...,m} h(I_k/I_{des}) \]

\[subject~to~~0 \leq p_j \leq p_{max},~j=1,...,m \]

with \(h(u)=max\{u,1/u\}\)
\(f_0\) is convex because maximum of convex functions is convex

additional constraints:
Does add 1 or 2 below complecate the problem?

1. no more than 50% total power is in 10 lamps
2. no more than half of lamps are on (\(p_j>0\))

• answer: whit (1), still easy to solve; whit (2), extremely difficult
• moral: (untrained) intuition doesn't always work; whitout the proper background very easy problems can appear quite similiar to very difficult

course goals and topics

goals

1. recognize/formulate problems (such as illumination problem) as convex optimization problems
2. develop code for problems of moderate size (1000 lamps, 5000 patchs)
3. characterize optimal solutin (optimal power distribution), give limits of performace, etc.

topics

1. convex sets, functions, optimization problems
2. examples and applications
3. algorithms

nonlinear optimization

...

2. Convex sets

• affine and convex sets
• some important example
• operations that preserve convexity
• genaralized inequalities
• separating and supporting hyperplanes
• dual cones and generalied inequalized

affine set

line through \(x_1, x_2\): all points

\[x=\theta x_1+(1-\theta)x_2~~~~(\theta\in R) \]

affine set: contains the line through any two distinct points in the set
example: soultion set of linear equation \(\{x|Ax=b\}\)
(conversely, every affine set can be expressed as solution set of system of linear equations)

convex set

line segment between \(x_1\) and \(x_2\): all points

\[x=\theta x+(1-\theta)x_2 \]

with \(0\le\theta\le1\)

convex set: contains any line segment between two points in the set

\[x_1,x_2\in C,~~0\le\theta\le1~~~\Longrightarrow~~~\theta x_1+(1-\theta)x_2\in C \]

examples:
略

convex combination and convex hull

convex combination of \(x_1,x_2,...,x_k\): any point \(x\) of the form

\[x=\theta_1x_1+\theta_2x _2+...+\theta_kx_k \]

with \(\theta_1+...+\theta_k=1,\theta_k\ge0\)

convex hull conv \(S\):set of all convex combination of points in \(S\)

convex cone

conic (nonnegative) combination of \(x_1\) and \(x_2\): any point of the form

\[x=\theta_1x_1+\theta_2x_2 \]

with \(\theta_1\ge0,\theta_2\ge0\)

convex cone: set that contains all conic combinations of points in the set

hyperplane and half-sapces

hyperplane: set of the form \(\{x|a^Tx=b\}(a\ne0)\)

halfspace: set of the form \(\{x|a^Tx\le b\}(a\ne0)\)

• \(a\) is the normal vector
• hyperplanes are affine and convex; halfspaces are convex

euclidean balls and ellipsoids

(euclipsoid) ball with center \(x_c\) and radius \(r\):

\[B(x_c,r)=\{x\vert~\Vert x-x_c\Vert^2\le r\}=\{x_c+ux\vert~\Vert u\Vert_2\le1\} \]

ellipsoid: set of the form

\[\{x\vert~(x-x_c)^TP^{-1}(x-x_c)\le1\} \]

with \(P\in S_{++}^n\) (\(i.e., P\) symmetic positive definite matrix)
other representation: \(\{x_c+Ax\vert \Vert u\Vert_2\le1\}\) with \(A\) suqare and nonsigular

norm balls and cones

norm: a function \(\Vert\cdot\Vert\) that satisfis

• \(\Vert x\Vert\ge0;~\Vert x\Vert=0\) if and only if \(x=0\)
• \(\Vert tx\Vert=\vert t\vert~\Vert x\Vert\) for \(t\in R\)
• \(\Vert x+y\Vert\le\Vert x\Vert+\Vert y\Vert\)
  notation:\(\Vert\cdot\Vert\) is general (unspecified) norm; \(\Vert\cdot\Vert_{symb}\) is particular norm

norm ball with center \(x_c\) and radius \(r:~\{x\vert~\Vert x-x_c\Vert\le r\}\)

norm cone: \(\{(x,t)\vert~\Vert x\Vert\le t\}\)
euclidean norm cone is called second-order cone;
norm balls and cones are convex

polyhedra

solution set of finitely many linear inequalities and equalities

\[Ax\preceq b,~~~~Cx=d \]

(\(A\in R^{m\times n},~C\in R^{p\times n},~\preceq\) is componentwise inequality)
polyhedron is intersection of finite number of halfspaces and hyperplanes

positive semidefinite cone

notation:

• \(S^n\) is set of symmetric \(n\times n\) matrices
• \(S_+^n=\{X\in S^n\vert X\succeq0\}:\) positive semidefinite \(n\times n\) matices

\[X\in S_+^n~~\Longleftrightarrow~~z^TXz\ge0~for~all~z \]

\(S_+^n\) is a convex cone

• \(S_{++}^n=\{X\in S^n\vert X\succ0\}:\) positive definite \(n\times n\) matrices

example: \(\left[\begin{array}{} x & y \\ y & z\end{array}\right]\in S_+^2\)

operations that preserve convexity

practical methods to establishing convexity of a set \(C\)

1. apply definition

\[x_1,x_2\in C,~0\le \theta \le1~~\Longrightarrow~~\theta x_1+(1-\theta) x_2\in C \]

2. show that \(C\) is obtained from simple convex sets (hyperplanes, halfspaces, norm balls, ...) by operations that preserve convexity

• intersection
• affine function
• perspective function
• linear-fractional function

intersection

the intersection of (any number of) convex sets is convex
example:

\[S=\{x\in R^m\vert~\vert p(t)\vert \le1~for~\vert t\vert\le\pi/3\} \]

where \(p(t)=x_1\cos t+x_2\cos 2t+...+x_m\cos mt\)

affine function

suppose \(f~:~R^n\rightarrow R^m\) is affine (\(f(x)=Ax+b~with~A\in R^{m\times n},~b\in R^m\))

• the image of a convex set under \(f\) is convex

\[S\subseteq R^n ~convex ~~\Longrightarrow~~f(S)=\{f(x)\vert x\in S\} ~convex \]

• the inverse image \(f^{-1}(C)\) of a convex set under \(f\) is convex

\[C\subseteq R^m ~convex\Longrightarrow f^{-1}(C)=\{x\vert x_1A_1+...x_mA_m\preceq B\}~convex \]

example:

• scaling, translationg, projection
• solution set of linear matrix inequality \(\{x\vert x_1A_1+...+x_mA_m\preceq B\}\) (with \(A_i,B\in S^p\))
• hyperbolic cone \(\{x\vert x^TPx\le(c^Tx)^2, c^Tx\ge0\}\) (with \(P\in S^n_{\perp}\))

perspective and linear-fractional function

perspective function \(P:R^{n+1}\rightarrow R^n\):

\[P(x,t)=x/t,~~~dom~P=\{(x,t)\vert x>0\} \]

images and inverse images of convex sets under perspective are convex

linear-fractional function \(f:R^n\rightarrow R^m\):

\[f(x)=\frac{Ax+b}{c^Tx+d},~~~dom~f=\{x\vert c^Tx+d>0\} \]

images and inverse images of convex sets under linear-fractional functions are convex
example of a linear-fractional function

\[f(x)=\frac{1}{x_1+x_2+1}x \]

generalized inequalities

a convex cone \(K\subseteq R^n\) is a proper cone if

• \(K\) is closed (contains its boundary)
• \(K\) is solid (has nonempty interior)
• \(K\) is pointed (contains no line)

examples

• nonnegtive orthant \(K=R_+^n=\{x\in R_n\vert x_i\ge0,i=1,...,n\}\)
• positive semidefinite cone \(K=S_+^n\)
• nonnegtive polynomials on \([0,1]\):

\[K=\{x\in R_n~\vert~ x_1+x_2t+x_3t^2+...+x_nt^{n-1}\ge0~for~t\in[0,1]\} \]

generalized inequality defined by a proper cone \(K\):

\[x\preceq_{K}y\Longleftrightarrow y-x\in K,~~~~~x\prec_{K}y\Longleftrightarrow y-x\in int~K \]

examples

• componentwise inequality (\(K=R_+^n\))

\[x\preceq_{R_+^n}y\Longleftrightarrow x_i\le y_i,~i=1,...,n \]

• martrix ineqaulity (\(K=S_+^n\))

\[X\preceq_{S_+^n}Y\Longleftrightarrow Y-X~positive~semidefinite \]

these two types are so common that we drop the subscript in \(\preceq_{K}\)

properties: many properties of \(\preceq_{K}\) are much similar to \(\le\) on \(R\), \(e.g.\),

\[x\preceq_{K}y,~u\preceq_{K}v\Longrightarrow x+u\preceq_{K}y+v \]

minimum and minimal elements

\(\preceq_{K}\) is not in general a linear ordering: we can have \(x\npreceq_{K}y\) and \(y\npreceq_{K}x\)

\(x\in S\) is the minimum element of \(S\) with respect to \(\preceq_{K}\) if

\[y\in S\Longrightarrow x\preceq_{K}y \]

\(x\in S\) is a minimal element of \(S\) with respect of \(\preceq_{K}\) if

\[y\in S,~y\preceq_{K}x\Longrightarrow y=x \]

example (\(K=R_+^2\))
\(x_1\) is the minimum element of \(S_1\)
\(x_2\) is a minimal elementof \(S_2\)

separating hyperplane thoerem

if \(C\) and \(D\) are disjoint convex sets, then there exists \(a\ne0,b\) such that

\[a^Tx\le b~for~x\in C,~~~a^Tx\ge b~for~ x\in D \]

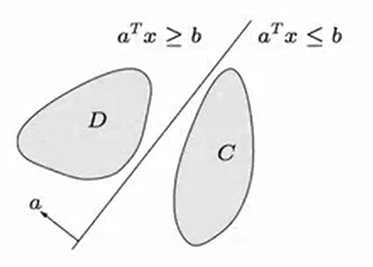
the hyperplane \(\{x\vert a^Tx=b\}\) separates \(C\) and \(D\)

strict separation requires additional assuptions (\(e.g.\), \(C\) is closed, \(D\) is a singleton)

supporting hyperplane theorem

supporting hyperplane to set \(C\) at boundary point \(x_0\):

\[\{x~\vert~a^Tx=a^Tx_0\} \]

where \(a\ne0\) and \(a^Tx\le a^Tx_0\) for all \(x\in C\)

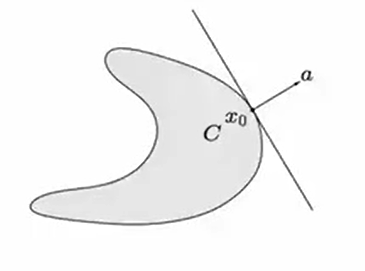
supporting hyperplane theorem: if \(C\) is convex, then there exists a supporting hyperplane at every boundary point of \(C\)

dual cones and generalized inequalities

dual cone of a cone \(K\):

\[K^*=\{y~\vert~y^Tx\ge0~for~all~x\in K\} \]

examples

• \(K=R_+^n:~K^*=R_+^n\)
• \(K=S_+^n:~K^*=S_+^n\)
• \(K=\{(x,t)~\vert~\Vert x\Vert_2\le t\}:~K^*=\{(x,t)~\vert~\Vert x\Vert_2\le t\}\)
• \(K=\{(x,t)~\vert~\Vert x\Vert_1\le t\}:~K^*=\{(x,t)~\vert~\Vert x\Vert_{\infty}\le t\}\)

first three examples are self-dual cones
dual cones of paper cones are proper, hence define generalized inequalities:

\[y\succeq_{K^*}0\Longleftrightarrow y^Tx\ge0~for~all~x\succeq_{K}0 \]

minimum and minimal elements via dual inequality

minimum element w.r.t. \(\preceq_{K}\)
\(x\) is minimum element of \(S\) if for all \(\lambda\succ_{K^*}0\), \(x\) is the unique minimizer of \(\lambda^Tz\) over \(S\)

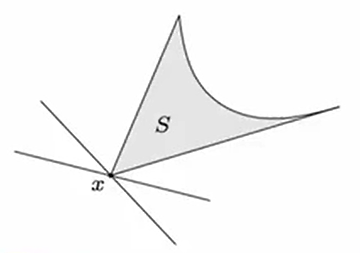
minimal element w.r.t. \(\preceq_{K}\)

• if \(x\) minimizes \(\lambda^Tz\) over \(S\) for some \(\lambda\succ_{K^*}0\), then \(x\) is minimal
• if \(x\) is a minimal element of a convex set \(S\), then there exists a nonzero \(\lambda\succeq_{K^*}0\) such that \(x\) minimizes \(\lambda^Tz\) over \(S\)

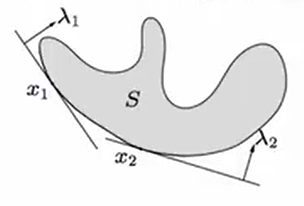
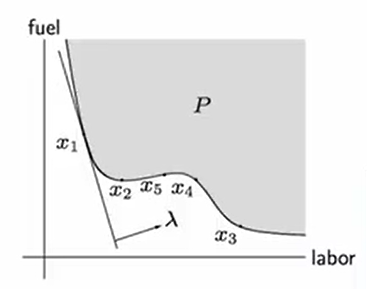
optimal production frontier

• different production methods use different amounts of resources \(x\in R^n\)
• production set \(P\): resource vectors \(x\) for all possibel production methods
• efficient (Pareto optimal) methods correspond to resource vectors \(x\) that are minimal w.r.t. \(R_+^n\)

example (\(n=2\))
\(x_1,x_2,x_3\) are efficient; \(x_4,x_5\) are not

Convex functions

• basic properties and examples
• oerations that preserve convexity
• the conjugation function
• quasiconvex functions
• log-concave and log-convex functions
• convexity with respect to generalized inequality

definition

\(f~:~R^n\rightarrow R\) is convex if dom \(f\) is a convex set and

\[f(\theta x+(1-\theta)y)\le \theta f(x)+(1-\theta)f(y) \]

for all \(x,y\in\) dom \(f,~0\le\theta\le 1\)

• \(f\) is concave if \(-f\) is convex
• \(f\) is strictly convex if dom \(f\) is convex and

\[f(\theta x+(1-\theta)y)< \theta f(x)+(1-\theta)f(y) \]

for \(x,y\in\) dom \(f,~x\ne y,~0<\theta<1\)

examples on \(\mathbf{R}\)

convex:

• affine: \(ax+b\) on \(\mathbf{R}\), for any \(a,b\in\mathbf{R}\)
• exponential: \(e^{ax}\), for any \(a\in\mathbf{R}\)
• powers: \(x^\alpha\) on \(\mathbf{R}_{++}\), for \(\alpha\ge1\) or \(\alpha\le0\)
• powers of absolute value: \(\vert x\vert^p\) on \(\mathbf{R}\), for \(p\ge1\)
• negative entropy: \(x\log x\) on \(\mathbf{R}_{++}\)

concave:

• affine: \(ax+b\) on \(\mathbf{R}\), for any \(a,b\in\mathbf{R}\)
• powers: \(x^\alpha\) on \(\mathbf{R}_{++}\), for \(0\le\alpha\le1\)
• logarithm: \(\log x\) on \(\mathbf{R}_{++}\)

example on \(\mathbf{R}^n\) and \(\mathbf{R}^{m\times n}\)

affine functions are convex; all norms are convex
example on \(\mathbf{R}^n\)

• affine function \(f{x}=a^Tx+b\)
• norms: \(\Vert x\Vert_p=(\sum\limits_{i=1}^n\vert x_i\vert^p)^{1/p}\) for \(p\ge1;~\Vert x\Vert_\infty = \max_k\vert x_k\vert\)
  example on \(\mathbf{R}^{m\times n}\) (\(m\times n\) matrices)
• affine function

\[f(X)=tr(A^TX)+b=\sum\limits_{i=1}^m\sum\limits_{j=1}^nA_{ij}X_{ij}+b \]

• spectral (maximum singular value) norm

\[f(X)=\Vert X\Vert_2=\sigma_{max}(X)=(\lambda_{max}(X^TX))^{1/2} \]

restriction of a convex function to a line

\(f:\mathbf{R}^n\rightarrow\mathbf{R}\) is convexif and only if the function \(g:\mathbf{R}\rightarrow\mathbf{R}\),

\[g(t)=f(x+tv),~~~~dom~g=\{t~\vert~x+tv\in dom~f\} \]

is convex (int \(t\)) for any \(x\in dom~f,~v\in\mathbf{R}^n\)
can check convexity of F by checking convexity of functions of one variable

example: \(f:\mathbf{S}^n\rightarrow\mathbf{R}\) with \(f(X)=\log\det X,~dom~f=\mathbf{S}_{++}^n\)

\[\begin{equation} \begin{split} g(t) & =\log\det(X+tV) \\ & =\log\det X+\log\det(I+tX^{-1/2}VX^{-1/2}) \\ & =\log\det X+\sum_{i=1}^n\log(1+t\lambda_i) \\ \end{split} \end{equation} \]

where \(\lambda_i\) are the eigenvalues of \(X^{-1/2}VX^{-1/2}\)
\(g\) is concave in \(t\) (for any choice of \(X\succ0,V\)); hence \(f\) is concave

extended-value extension

(extended value extension: 拓展值延伸)
extended-value extension \(\tilde{f}\) of \(f\) is

\[\tilde{f}(x)=f(x),~~x\in dom~f,~~~~~~\tilde{f}(x)=\infty,~~x\notin dom~f \]

often simplifies notation; for example, the condition

\[0\le\theta\le1~\Longrightarrow~\tilde{f}(\theta x+(1-\theta)y)\le\theta\tilde{f}(x)+(1-\theta)\tilde{f}(y) \]

(as an inequality in \(\mathbf{R}\cup\{\infty\}\)), means the same as the two conditions

• \(dom~f\) is convex
• for \(x,y\in dom~f\),

\[0\le\theta\le1~\Longrightarrow~f(\theta x+(1-\theta)y)\le\theta f(x)+(1-\theta)f(y) \]

first-order condition

\(f\) is differentiable if dom f is open and the gradient

\[\nabla f(x)=\left(\frac{\partial f(x)}{\partial x_1},\frac{\partial f(x)}{\partial x_2},...,\frac{\partial f(x)}{\partial x_n}\right) \]

exists at each \(x\in dom~f\)
1st-order condition: differentiable \(f\) with convex domain is convex if

\[f(y)\ge f(x)+\nabla f(x)^T(y-x)~for~all~x,y\in dom~f \]

first-order approximation of \(f\) is global underestimator

second-order condition

\(f\) is twice differentiable if dom f is open and the Hessian \(\nabla^2f(x)\in\mathbf{S}^n\),

\[\nabla^2f(x)_{ij}=\frac{\partial^2f(x)}{\partial x_i\partial x_j},~~i,j=1,...,n, \]

exists at each \(x\in dom~f\)

2nd-order conditions: for twice differentiable \(f\) with convex domain

• \(f\) is convex if and only if

\[\nabla^2f(x)\succeq0~for~all~x\in dom~f \]

• if \(\nabla^2f(x)\succ0~\) for all \(x\in dom~f\), then \(f\) is strictly convex

examples

quadratic function: \(f(x)=(1/2)x^TPx+q^Tx+r\) (with \(P\in\mathbf{S}^n\))

\[\nabla f(x)=Px+q,~~~~\nabla^2f(x)=P \]

convex if \(P\succeq0\)
least-suqares objective: \(f(x)=\Vert Ax-b\Vert_2^2\)

\[\nabla f(x)=2A^T(Ax-b),~~~~\nabla^2f(x)=2A^TA \]

convex (for any A)
quadratic-over-linear: \(f(x,y)=x^2/y\)

\[\nabla^2f(x,y)=\frac{2}{y^3}\left[\begin{array}{cc|r}y \\ -x \end{array}\right]\left[\begin{array}{cc|r}y \\ -x \end{array}\right]^T\succeq0 \]

convex for \(y>0\)

log-sum-exp \(f(x)=\log\sum\limits_{k=1}^n\exp x_k\) is convex

\[\nabla^2f(x)=\frac{1}{\mathbf{1}^Tz}diag(z)-\frac{1}{(\mathbf{1}^Tz)^2}zz^T~~~~~~(z_k=\exp x_k) \]

to show \(\nabla^2f(z)\succeq0\), we must werify that \(v^T\nabla^2f(x)v\ge0\) for all \(v\):

\[v^T\nabla^2f(x)v=\frac{(\sum_kz_kv_k^2)(\sum_kz_k)-(\sum_kv_kz_k)^2}{(\sum_kz_k)^2}\ge0 \]

since (\((\sum_kv_kz_k)^2\le(\sum_kz_kv_k^2)(\sum_kz_k)\)) (from Cauchy-Schwarz inequality)

geometric mean: \(f(x)=(\prod_{k=1}^nx_k)^{1/n}\) on \(\mathbf{R}_{++}^n\) is concave (similar proof as for log-sum-exp)

epigraph and sublevel set

（epigraph：上境图；sublevel set：下水平集）
\(\alpha\)-sublevel set of \(f:\mathbf{R}^n\rightarrow\mathbf{R}\):

\[C_\alpha=\{x\in dom~f~|~f(x)\le\alpha\} \]

sublevel sets of convex functions are convex (converse is false)
epigraph of \(f:\mathbf{R}^n\rightarrow\mathbf{R}\):

\[epi~f=\{(x,t)\in\mathbf{R}^{n +1}~|~x\in dom~f,f(x)\le t\} \]

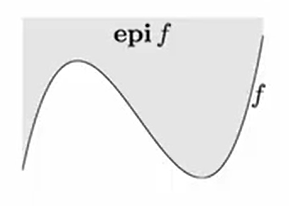
\(f\) is convex if and only if \(epi~f\) is a convex set

Jense's inequality

basic inequality: if \(f\) is convex, then for \(0\le\theta\le1\),

\[f(\theta x+(1-\theta)y)\le\theta f(x)+(1-\theta)f(y) \]

extension: if \(f\) is convex, then

\[f(\mathbf{E}z)\le\mathbf{E}f(z) \]

for any random variable \(z\)

basic inequality is special case with discrete distribution

\[\mathbf{prob}(z=x)=\theta,~~~~~~\mathbf{prob}(z=y)=1-\theta \]

operations that preserve convexity

practical methods for establishing convexity of a function

1. verify definition (often simplified restricting to a line^<1>)
2. for twice differentiable function, show \(\nabla^2f(x)\succeq0\)
3. show that \(f\) is obtainted form simple convex functions by operation that preserve convexity

• nonnegative weighted sum
• composition with affine function
• pointwise maximum or supremum
• composition
• minimization
• perspective

^<1>: Generally we know that a function is convex it is convex even after we restrict it to a line. "Restricting a function to a line" simply means that you draw a line in the domain of that function and evaluate the function along that line.

positive weighted sum & composition with affine function

nonnegative multipe: \(\alpha f\) is convex if \(f\) is convex, \(\alpha \ge 0\)
sum: \(f_1+f_2\) convex if \(f_1,~f_2\) convex (extends to infinite sums and integrals)
composition with affine function: \(f(Ax+b)\) is convex if \(f\) is convex

examples:

• log barrier for linear inequalities

\[f(x)=-\sum\limits_{i=1}^m\log(b_i-a_i^Tx),~~~~~~dom~f=\{x\vert a_i^Tx < b_i,~i=1,...,m\} \]

• (any) norm of affine function: \(f(x) = \Vert Ax+b\Vert\)

pointwise maximum

if \(f_1,...,f_m\) is convex, then \(f(x)=max\{f_1(x),...,f_m(x)\}\) is convex

examples

• piecewisw-linear function: \(f(x)=\max\limits_{i=1,...,m}(a_i^Tx+b_i)\)
• sum of \(r\) largest components of \(x\in\mathbf{R}^n\):

\[f(x)=x_{[1]}+x_{[2]}+...+x_{[r]} \]

is convex (\(x_{[i]}\) is \(i\)th largest component of \(x\))
proof:

\[f(x)=\max\{x_{i_1}+x_{i_2}+...+x_{i_r}\vert 1\le i_1< i_2< ...< i_r \le n \} \]

pointwise supremum

(supremum：上界)
if \(f(x,y)\) is convex in \(x\) for each \(y\in\mathcal{A}\), then

\[g(x)=\sup\limits_{y\in\mathcal{A}}f(x,y) \]

is convex
examples

• support function of a set \(C:S_C(x)=\sup_{y\in C}y^Tx\) is convex

• distance to farthest point in a set \(C\):

\[f(x)=\sup\limits_{y\in C}\Vert x-y\Vert \]

• maximun eigenvalue of symmetric matrix: for \(X\in\bf{S}^n\),

\[\lambda_{max}(X)=\sup\limits_{\Vert y\Vert_2=1}y^TXy \]

composition with scalar functions

composition of \(g:\bf{R}^n\rightarrow\bf{R}\) and \(h:\bf{R}\rightarrow\bf{R}\):

\[f(x)=h(g(x)) \]

\(f\) is convex if:
\(g\) convex, \(h\) convex, \(\tilde{h}\) nondecreasing;
\(g\) convave, \(h\) convex, \(\tilde{h}\) nonincreasing

• proof (for \(n=1\), differentiable \(g,h\))

\[f''(x)=h''(g(x))g'(x)^2+h'(g(x))g''(x) \]

• note: monotonicity must hold for extended-value extension \(\tilde{h}\)

examples

• \(\exp g(x)\) is convex if \(g\) is convex
• \(1/g(x)\) is convex if \(g\) is concave and positive

vector composition

composition of \(g:\bf{R}^n\rightarrow\bf{R}^k\) and \(h:\bf{R}^k\rightarrow\bf{R}\):

\[f(x)=h(g(x))=h(g_1(x),...,g_k(x)) \]

\(f\) is convex if
\(g_i\) convex, \(h\) convex, \(\tilde{h}\) nondecreasing in each argument
\(g_i\) concave, \(h\) convex, \(\tilde{h}\) nonincreasing in each argument
proof (for \(n=1\), differentiable \(g,h\))

\[f''(x)=g'(x)^T\nabla^2h(g(x))g'(x)+\nabla h(g(x))^Tg''(x) \]

examples

• \(\sum_{i=1}^m\log g_i(x)\) is concave if \(g_i\) are concave and positive
• \(\log\sum_{i=1}^m\exp g_i(x)\) is convex if \(g_i\) is covex

minimization

(infimum: 下界；Schur complement（舒尔补）：https://blog.csdn.net/sheagu/article/details/115771184)
if \(f(x,y)\) is convex in \((x,y)\) and \(C\) is a convex set, then

\[g(x)=\inf\limits_{y\in C}f(x,y) \]

is convex
examples

• \(f(x,y)=x^TAx+2x^TBy+y^TCy\) with

\[\left[ \begin{matrix} A & B \\ B^T & C \end{matrix} \right]\succeq0,~~~~C\succ0 \]

minimizing over \(y\) gives \(g(x)=\inf_yf(x,y)=x^T(A-BC^{-1}B^T)x\) \(g\) is convex, hence Schur complement \(A-BC^{-1}B^T\succeq0\)

-distance to a set: \(dist(x,S)=\inf\limits_{y\in S}\Vert x-y\Vert\) is convex if \(S\) is convex

perspective

the perspective of a function \(f:\bf{R}^n\rightarrow\bf{R}\) is the function \(g:\bf{R}^n\times\bf{R}\rightarrow\bf{R}\),??有问题！

\[g(x,t)=tf(x/t),~~~~~~dom~g=\{(x,t)\vert x/t\in dom~f,t>0\} \]

\(g\) is convex if \(f\) is convex

examples

• \(f(x)=x^Tx\) is convex; hence \(g(x,t)=x^Tx/t\) is convex for \(t>0\)
• negative logrithm \(f(x)=-\log x\) is convex; hence relative entropy \(g(x,t)=t\log t-t\log x\) is convex on \(\bf{R}_{++}^2\)
• if \(f\) is convex, then

\[g(x)=(c^Tx+d)f\left((Ax+b)/(c^Tx+d)\right) \]

is convex on \({x\vert c^Tx+d>0, (Ax+b)/(c^Tx+d)\in dom~f}\)

the conjugate function

the conjugate of a function \(f\) is

\[f^*(y)=\sup\limits_{x\in dom~f}(y^Tx-f(x)) \]

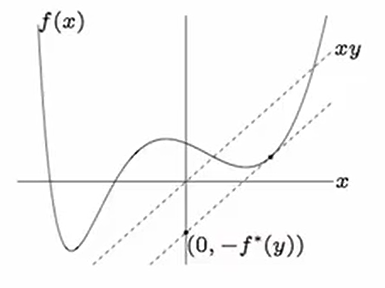
• \(f^*\) is convex (even if \(f\) is not)
• will be useful in chapter 5

examples

• negative logarithm \(f(x)=-\log x\)

\[\begin{align*} f^*(y)&=\sup\limits_{x>0}(xy+\log x) \\ &=\begin{cases} -1-\log(-y) & y<0 \\ \infty & \rm{otherwise} \end{cases} \end{align*} \]

• strictly convex quadratic \(f(x)=(1/2)x^TQx\) with \(Q\in\bf{S}_{++}^n\)

\[\begin{align*} f^*(y)&=\sup\limits_x(y^Tx-(1/2)x^TQx) \\ &=\frac{1}{2}y^TQ^{-1}y \end{align*} \]

quasiconvex functions

\(f:\bf{R}^n\rightarrow\bf{R}\) is quasiconvex if \(dom~f\) is convex and the sublevel sets

\[S_\alpha=\{x\in dom~f\vert f(x)\le\alpha\} \]

are convex for all \(\alpha\)

• \(f\) is quasiconcave if \(-f\) is quasiconvex
• \(f\) is quasilinear if it is quasiconvex and quasiconcave

注：拟凸

examples

• \(\sqrt{\vert x\vert}\) is convex on \(\bf{R}\)
• ceil\((x)=\inf\{z\in\bf(Z)\vert z\ge x\}\) is quasilinear
• \(\log x\) is quasilinear on \(\bf{R}_{++}\)
• \(f(x_1,x_2)=x_1x_2\) is quasicave on \(\bf{R}_{++}^2\)
• linear-fractional function

\[f(x)=\dfrac{a^Tx+b}{c^Tx+d},~~~~dom~f=\{x\vert c^Tx+d\ge0\} \]

is quasilinaer

• distance ratio

\[f(x)=\dfrac{\Vert x-a\Vert_2}{\Vert x-b\Vert_2},~~~~~dom~f=\{x\vert\Vert x-a\Vert_2\le\Vert x-b\Vert_2\} \]

is quasiconvex
注：距离比

internal rate of return
略

注：内部收益率

properties

modified Jeson inequality: for quasiconvex \(f\)

\[0\le\theta\le1\Longrightarrow f(\theta x+(1-\theta)y)\le\max\{f(x),f(y)\} \]

first-order condition: differentiable \(f\) with convex domain is quasiconvex if

\[f(y)\le f(x)\Longrightarrow\nabla f(x)^T(y-x)\le0 \]

sums of quasiconvex functions are not necessarily quasiconvex

log-concave and log-convex functions

a positive function \(f\) is log-concave if \(\log f\) is concave:

\[f(\theta x+(1-\theta)y)\ge f(x)^\theta f(y)^{1-\theta}~~for~0\le\theta\le1 \]

\(f\) is log-covex if \(\log f is convex\)

• powers: \(x^a\) on \(\bf{R}_{++}\) is log-convex for \(a\le0\),log-convave for \(a\ge0\)
• many common probability densities are log-concave, \(e.g.\), normal:

\[f(x)=\dfrac{1}{\sqrt{(2\pi)^n\det\sum}}e^{-\frac{1}{2}(x-\tilde{x})^T\sum^{-1}(x-\tilde{x})} \]

上式表示什么？？？？

• cumulative Gaussian distribution function \(\Phi\) is log-cocave

\[\Phi(x)=\dfrac{1}{\sqrt{2\pi}}\int_{-\infty}^{x}e^{-u^2/2}du \]

properties of log-concave functions

• twice differentiable \(f\) with convex domain is log-concave if and only if

\[f(x)\nabla^2f(x)\preceq\nabla f(x)\nabla f(x)^T \]

for all \(x\in dom~f\)

• product of log-concave functions is log-concave
• sum of log-concave is not always log-concave
• integration：if \(f:\bf{R}^n\times\bf{R}^m\rightarrow\bf{R}\) is log-concave, then

\[g(x)=\int f(x,y)dy \]

is log-concave (not easy to show)

consequences of integration property

• convolution \(f*g\) of log-concave functions \(f,g\) is log-concave

\[(f*g)(x)=\int f(y)g(x-y)dy \]

• if \(C\subseteq \bf{R}^n\) concex and \(y\) is a random variable with log-concave pdf then

\[f(x)=prob~(x+y\in C) \]

is log-concave
proof: write \(f(x)\) as integral of product of log-concave functions

\[f(x)=\int g(x+y)p(y)dy,~~~~g(u)=\begin{cases} 1&u\in C \\ 0&u\notin C, \end{cases} \]

\(p\) is pdf of \(y\)

注：pdf（probability density function）概率密度函数；prob() 求概率运算?

example: yield function

\[Y(x)=prob~(x+w\in S) \]

• \(x\in\bf{R}^n\): nominal parameter vlues for product
• \(w\in\bf{R}^n\): random variations of parameters in manufactured peoduct
• \(S\): set of acceptable values

if \(S\) is convex and \(w\) has a log-concave pdf, then

• Y is log-concave
• yield regions \(\{x\vert Y(x)\ge\alpha\}\)

convexity with respect to generalized inequalities

\(f:\bf{R}^n\rightarrow\bf{R}^m\) is \(K\)-convex if \(f\) is convex and

\[f(\theta x+(1-\theta)y)\preceq_K\theta f(x)+(1-\theta)f(y) \]

for \(x,y\in dom~f,0\le\theta\le1\)

example \(f:\bf{S}^m\rightarrow\bf{S}^m\), \(f(X)=X^2\) is \(\bf{S}_+^m\)-convex

proof: for fixed \(z\in\bf{R}^m\), \(z^TX^2z=\Vert Xz\Vert_2^2\) is convex in \(X\), \(i.e.\),

\[z^T(\theta X+(1-\theta)Y)^2z\le\theta z^TX^2z+(1-\theta z^TY^2z) \]

for \(X,Y\in\bf(S)^m\), \(0\le\theta\le1\)
therefore \(f(\theta X+(1-\theta)Y)^2\preceq_K\theta X^2+(1-\theta)Y^2\)