l1 和l2正则详解

最近有在面试一些公司，有被问题关于lr的一些问题，还有包括L1和L2正则的一些问题，回答的不是很好，发现有时候自己明白了，过了一阵子又会忘记，现在整理整理，写成博客防止以后再次忘记

我们基于lr模型来讲正则，首先y=sigmiod（wx+b）这是基本的lr模型。损失函数为0,1交叉熵，

 

 

 

 

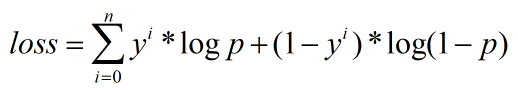
L1正则：

 

l2 正则： 

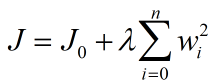
使用等高线图来表示原目标函数的图像为（假定只有两个参数）：

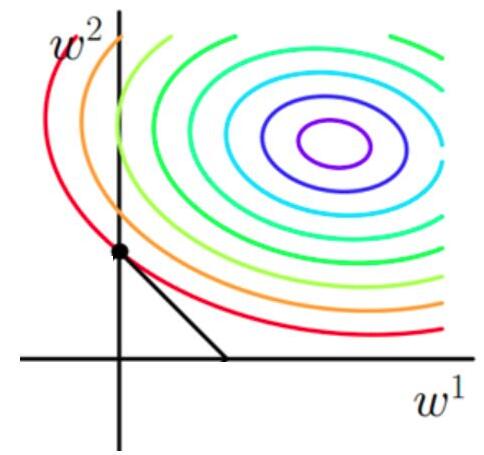
 也就是说，当参数 w1与w2w1与w2 取值为图像中最里面那个紫色圆圈上的值时，可以使得原目标函数最小。   当加上L1正则项之后，目标函数图像为：

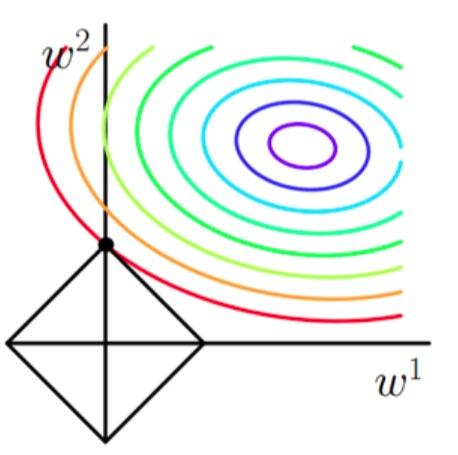
  当加上L2正则项之后，目标函数图像为：

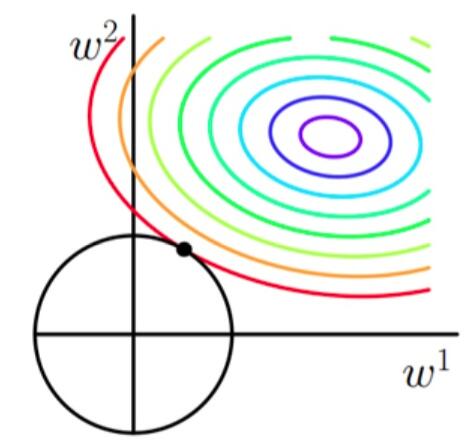
　　第一个图中菱形即为 ∑2j=1|wj|=F∑j=12|wj|=F ，而第二个图中圆形即为 ∑2j=1w2j=F∑j=12wj2=F 。代表这个菱形（圆形）上的点算出来的 ∑2j=1|wj|或∑2j=1w2j∑j=12|wj|或∑j=12wj2 都等于某个值 FF 。此时若要使得目标函数最小，就需要满足两个条件：（1）参数值在等高线上的圆圈越来越接近中心的紫色圆圈，（2）菱形越小越好（ FF 越小越好）。   那么如何取得一个恰好的值，能够满足以上两个条件呢？我们先来看下下面这个图（以L1正则化为例）：

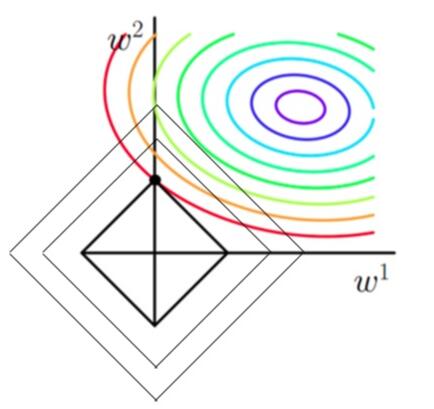
讨论为什么l1正则之后的特征参数是稀疏的？

因为观察发现**几乎对于很多原函数等高曲线，和某个菱形相交的时候及其容易相交在坐标轴（比如上图）： 

另外一考虑正则项导数的情况，l1正则的倒数不是-1就是1，所以会很容易收敛到0；然而l2正则的倒数是线性函数，w越靠近0的话导数就越小，这会让w无限趋近于0，但不会收敛到0；

 

l1正则不可导怎么处理？

 

坐标轴下降法

 

 

 

 

 

 

 

参考链接: https://www.cnblogs.com/lliuye/p/9354972.html