梯度下降算法的理解

如求函数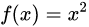的最小值。利用梯度下降的方法解题步骤如下：
1、求梯度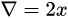
2、向梯度相反的方向移动，如下

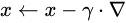
，其中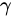， 为步长。如果步长足够小，则可以保证每一次迭代都在减小，但可能导致收敛太慢，如果步长太大，则不能保证每一次迭代都减少，也不能保证收敛。
3、循环迭代步骤2，直到的值变化到使得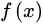在两次迭代之间的差值足够小，比如0.00000001，也就是说，直到两次迭代计算出来的 基本没有变化，则说明此时 已经达到局部最小值了。
4、此时，输出 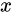，这个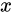就是使得函数 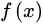最小时的x 的取值 。

以上案例来自百度百科：梯度下降
理解上有点抽象。下面用代码分析下：
初始化步长step和初始值x，f_change为前后的y值变化相当于y。k梯度下降迭代次数
`

step即为梯度下降API的学习率

step=0.1
x=2
k=0

f_change=x^2
f_current=x^2

while f_change>0.000000001:
//下降的x值=x-函数梯度（一阶导数）乘以step，（即代表下降的速度2x步长）
x=x-step * 2* x(2x为该函数的一阶导数)
//f（x）=f(x2)-f(x1)，即为y变化后的f_change，前后y值的变化差
f_change=f_current-x^2（这里是指“下降的策略”，此案例采用最简单的“差值”）
//f_current为当前的y值
f_current=x^2
k=k+1
print(k)
print(xLst)
print(f_currentLst)
print(f_changeLst)
print(xLst.index(min(xLst)))
print(f_currentLst.index(min(f_currentLst)))
print(f_changeLst.index(min(f_changeLst)))

总共循环49次，至到找到x,f(x)，且y的前后差值为最小值结束。即数值收敛到最小值。

以上代码注意的地方：
1）x=x-step2x，由于x的初始值为正整数且其一阶导数为正数取值，故step的取值为正数且小于1的数值才会使得X值不断下降。否则为梯度上升。
2）f_change变化速度取决于x梯度下降的速度，而X梯度下降的速度是由step决定的。（因为其一阶导数即梯度确定的，因为函数已确认故其一阶导数也是确定的）

梯度算法的前提是函数可导，那对于不可导或导数计算复杂函数如何处理呢？
参照知乎讨论“关于loss函数没导数怎么办？”
https://www.zhihu.com/question/268163416?sort=created