伽玛分布与泊松分布、指数分布的关系

指数分布:要等到一个随机事件发生，需要经历多久时间。
伽玛分布:要等到n个随机事件发生，需要经历多久时间。所以，伽玛分布可以看作是n个指数的独立随机变量的加总。
泊松分布：在特定时间里发生n个事件的概率。
2、从公式来看：

X∼Gamma(α,λ)，概率公式如下：

将a=1时，=1，代入到伽玛公式，就变成了指数分布:

Gamma分布的特殊形式
当形状参数α=1时，伽马分布就是参数为γ的指数分布，X~Exp（γ）
当α=n/2，β=1/2时，伽马分布就是自由度为n的卡方分布，X^2(n)

3、从统计指标来看：

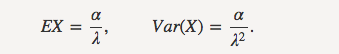
这就是 n(alpha)倍的指数分布的期望啊！
补充一下：如果想更好地理解，还可以加入泊松分布，泊松分布解决的是“在特定时间里发生n个事件的机率”。所以可以脑洞大开地想：伽玛分布=指数分布＊泊松分布。看看pdf的表达式，自己换一个写法就会发现伽玛把exponential和poisson的公式揉到一起了。

伽玛分布的应用案例：
冗余系统（standby redundant system）假设有一个系统有个部件，但实际需要的只有一个（其余的是备用）。当一个部件失效时，另一个自动接管。因此，只有当所有个部件都失效时，系统才会崩溃。在一定假设下，Gamma分布可以用来描述这样一个系统的寿命。

作者：知乎用户
链接：https://www.zhihu.com/question/34866983/answer/191286772
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。