泊松分布
去年12月,美国康涅狄格州发生校园枪击案,造成28人死亡。
资料显示,1982年至2012年,美国共发生62起(大规模)枪击案。其中,2012年发生了7起,是次数最多的一年。
去年有这么多枪击案,这是巧合,还是表明美国治安恶化了?
前几天,我看到一篇很有趣的文章,使用"泊松分布"(Poisson distribution),判断同一年发生7起枪击案是否巧合。
让我们先通过一个例子,了解什么是"泊松分布"。
例如:已知某家小杂货店,平均每周售出2个水果罐头。请问该店水果罐头的最佳库存量是多少?
假定不存在季节因素,可以近似认为,这个问题满足以下三个条件:
(1)顾客购买水果罐头是小概率事件。
(2)购买水果罐头的顾客是独立的,不会互相影响。
(3)顾客购买水果罐头的概率是稳定的。
在统计学上,只要某类事件满足上面三个条件,它就服从"泊松分布"。
泊松分布的公式如下:
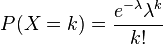
各个参数的含义:
**P:每周销售k个罐头的概率。
X:水果罐头的销售变量。
k:X的取值(0,1,2,3...)。
λ:每周水果罐头的平均销售量,是一个常数,本题为2。**
根据公式,计算得到每周销量的分布:

从上表可见,如果存货4个罐头,95%的概率不会缺货(平均每19周发生一次);如果存货5个罐头,98%的概率不会缺货(平均59周发生一次)。
案例2:
例有一繁忙的汽车站,每天有大量汽车通过,设每辆汽车,在一天的某段时间内出事故的概率为0.0001,在每天的该段时间内有1000 辆汽车通过,问出事故的次数不小于2的概率是多少?
设1000 辆车通过,出事故的次数为 X ,则X~b(1000,0.0001),
可利用泊松定理计算,λ=1000×0.0001=0.1
P{X≥2}≈1-e(-0.1)/0!-0.1×e(-0.1)/1!=0.0047
注意:
- λ是指平均发生的次数,即泊松分布中影响的唯一因子。第一个案例中,直接告诉了λ值,即平均卖的罐头。第二个案例中,没有直接给出平均值,但发生的概率和参与的样本数。故平均值λ=样本数*发生概率
- 第一个案例中求的是最佳库存量,为泊松分布概率的累计概率,即缺货概率。第二个案例中出的的发生次数小小于2的概率,即X大于或等于2的取值时的概率,因为总概率是1,将1-P(x=0)-P(x=1),即为题目所求的目标概率。
以下是泊松分布的代码