中心极限定理案例理解

定理一（独立同分布的中心极限定理）设随机变量X1,X2,..,X3,..相互独立，服从同一分布，且具有数学期望和方差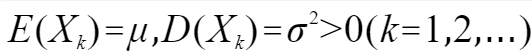
，则随机变量之和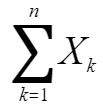的标准化变量的分布函数对于任意x满足

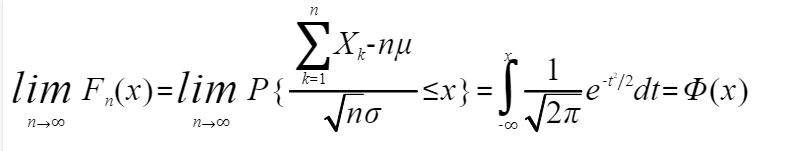
案例1：一加法器同时收到20个噪声电压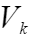（k=1,2,...,20）,设它们是相互独立的随机变量，且都在区间（0，10）上服从均匀分布，记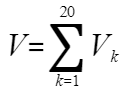,求P{V>105}的近似值。
分析：目标： 某个事项总值达到目标值的概率，即变量的分布函数。 求一个加法器电压大于105的概率是多少。（即20个噪声电压加起来大于105的概率）
事项的特点：一个事项，多个变量组成。一个加法器，20个变量。
变量的分布函数特点：变量的取值范围:变量的取值范围是（0，10）均匀分布，故变量的概率为1/10，f(x)=1/10*x
已知均匀分布的期望和方差公式如下：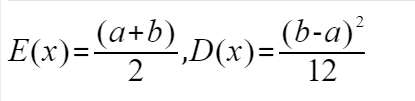

故等到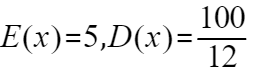
要算一个加法器电压大于105的概率是多少，即\({P \left\{ v > 105 \left\} =p \left\{ \frac{{v-20 \times 5}}{{ \left( 10/\sqrt{{12}} \left) \sqrt{{20}}\right. \right. }} > \frac{{105-20 \times 5}}{{ \left( 10/\sqrt{{12}} \left) \sqrt{{20}}\right. \right. }} \right\} \right. \right. }\)
根据目标总电值可以算到标准化变量0.387，而总电值的标准化变量>0.387的概率即为P{V>105}的概率。这里的计算根据定理一，转化为正态分布来计算。

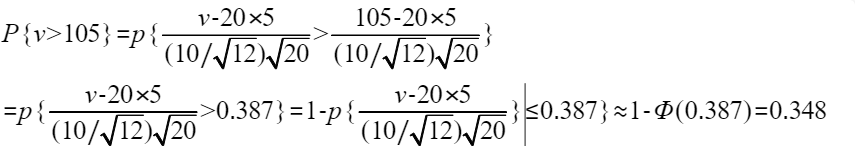
注意将大于号转换成小于等于号之后，可直接利用定理一公式代入了。

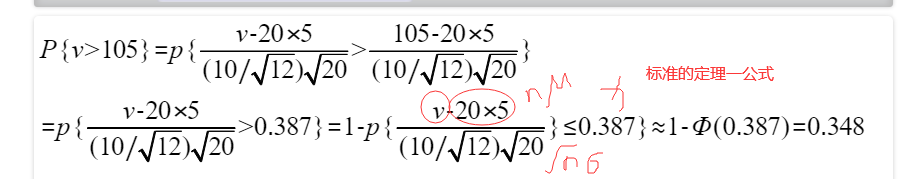
故这类题目都可以直接套用定理一公式。
总结:
1.计算一个事物的总概率
2.该事物有多个变量组成，这些变量在特定的区间是均匀分布的、
3.根据均匀分布的特点，计算出期望和方差
4.根据目标值和期望和方差，可直接近似于正态分布。

5.如果求大于某个目标值的概率，则结果=1-正态分布（第四步的值），如果求小于或等于某个目标值，则其概率结果=正态分布（第四步的值）

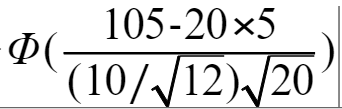
其他类似的习题
习题一.据以往的经验，某种电器元件的寿命服从均值为100h的指数分布，现随机地取16只，设它们的寿命是相互独立的，求这16只元件寿命的总和大于1920的概率。
分析：1）目标： 某个事项总值达到目标值的概率 2）一个事项，多个变量组成，这里有16个变量3）变量的分布函数特点：指数函数分布

4）根据变量的概率密度函数特点得到期望和方差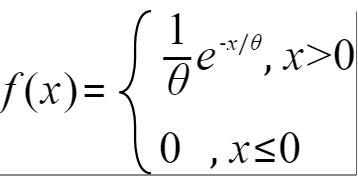

注：指数函数中的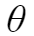代表每单位时间内发生某事件的次数、也可以理解为某个事件的寿命、某个事件的放电次数等。
5）由于每个电器元件独立的。适应定理一

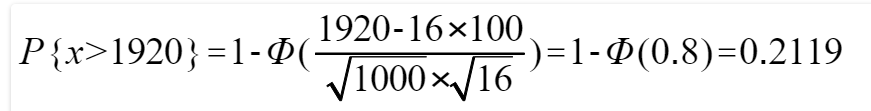
习题二、一保险公司有10000个汽车投保人，每个投保人索赔金额的数学期望为280美元，标准差为800美元，求索赔总金额超过2700000美元的概率。
分析：1）目标：某个事项总值达到目标值的概率 2）一个事件，多个变量组成，这里有10000变量 3）已告知期望和方差 3）由于每个变量，投保人是独立的，故适应于定理一。

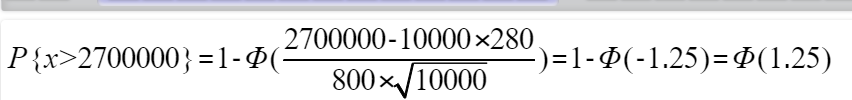
习题三、一公司有50张签约保险单，各张保险单的索赔金额为Xi，i=1,2,...,50(以千美元计）服从韦布尔分布，均值E（x)=5,方差D（x）=6,求50张保险单索赔的合计金额大于300的概率（设各保险单索赔金额是相互独立的）。
分析:1）目标：某个事项总值达到目标值的概率 2）一个事件，多个变量组成，这里有50变量 3）已告知期望和方差 3）由于每个变量独立的，故适应于定理一。

定理三：（棣莫费-拉普拉斯定理）设随机变量服从参数为n,p(0<p<1)的二项分布，则对于任意x，有

案例：一船舶在某海区航行，已知每遭受一次波浪的冲击，纵摇角大于3度的概率为p=1/3，若船舶遭受了90000次波浪冲击，问其中有29500至30500次纵摇角度大于3度的概率是多少？
分析：1）目标:某个事项总值达到的目标值的概率，求的是区间目标概率 2）事件遭受海浪，要么遭受，要么不遭受，故服从二项分布。即在第i次试验中事件A发生的次数，n=90000,p=1/3 3）根据二项分布，适应于定理三 4）代入公式，近似于正态分布得到目标值的概率

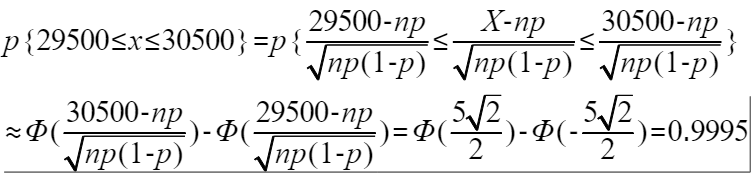
总结:
1.计算一个事物的总概率
2.该事物的随机变量服从二项分布，即能等到n值和p值
3.根据均匀分布的特点，计算出期望和方差
4.根据n值和p值 ，利于定理三可直接近似于正态分布。
5.如果求大于某个目标值的概率，则结果=1-正态分布（第四步的值），如果求小于或等于某个目标值，则其概率结果=正态分布（第四步的值）。如果是区间a,b(b>a)目标值,则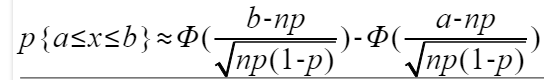
得到的值
其他类似的习题
习题一：有一批建筑房屋用的木柱，其中80%的长度不小于3m,现在从这批木柱中随机地取100根，求其中至少有30根要短于3m的概率。
分析:1)目标：某个事项总值达到目标值的概率，即30根短于3m的概率。求要大于30根的目标数 2）一个木柱，要不小于3m，要不长于3m，故服从二项分布，n=100,p=(1-80%)=0.2(短于3m的概率)，3)根据二项分布，适应于定理三 4）代入公式

习题二：对于一个学生而言，来参加家长会的家长人数是一个随机变量，设一个学生无家长、1名家长、2名家长来参加会议的概率分别是0.05,0.8,0.15。若学校共有400名学生，设各学生参加会议的家长人数相互独立，且服从同一分布。1）求参加会议的家长人数X超过450的概率。2)求有1名家长来参加会议的学生人数不多于340的概率。
分析：1）目标：某个事项总值达到目标值的概率 2）某个事项的概率分布，不符合二项，也不符合均匀分布，但事项独立。

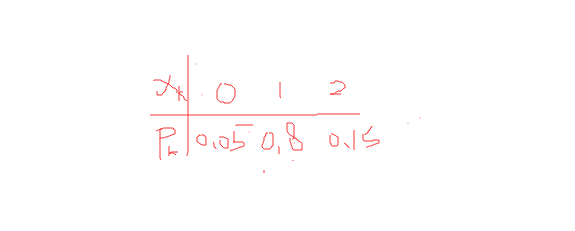
3）根据第2步的分析，得到期望值和方差值。E(x)=00.05+10.8+2*0.15=1.1,D(x)=0.19
4）要算第一问，则可以根据定理一

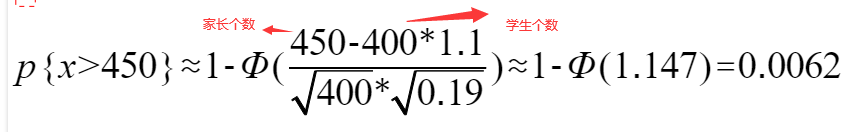
第2问：一名家长参加会议的学生人数，y`b(400,0.8),由定理三。为什么是二项分布，即要不一名家长加，要不一名家长不参加，故看成二项分布，适应定理三。
注意：注意第1问题和第2问的区别，其学生个数与家长个数的联系和区别。
第1问的目标概率是指参加家长人数的概率，家长人数是相互独立，故算是独立分布。
第2问的目标概率是指带1名家长的学生人数概率，其目标变量是学生是否带家长，学生要么带一名家长，要么不带一名家长，故是二项分布。已知学生带一名家长的概率是0.8。

总结：
中心极限定理，题目分析时重点要分析被求目标值的概率与目标变量的关系以及函数分布的期望和方差。