概率论和数理统计_07_频率学派和贝叶斯学派基本知识

频率学派与贝叶斯学派都是解决统计推断问题。
频率学派也称为经典学派。此学派将事件发生的概率看出一种固定的值。
贝叶斯学派将事件发生的概率看出一个随机变量。
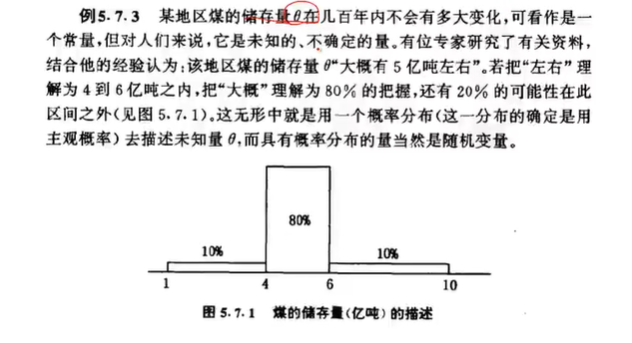
例如:对某个煤矿的煤存储里描述中，经典学派描述煤存储A=10Kg，。贝叶斯对煤存储A描述在10KG左右，然后根据历史资料或其他信息，推测2<A<8，概率为80%，其他情况概率为20%。

统计推断有三个要点:1.抽样分析 2.参数估计 3.假设检验。三个重要的信息源：1.总体信息 2.样本信息 3.先验信息
两个学派都会用到总体信息和样本信息，而贝叶斯学派增加了'先验信息“这一信息源的利用。

贝叶斯统计案例1：拉普拉斯在1786年研究了巴黎男婴的出生率是否大于0.5.

第一步：似然函数
设婴儿出生的事件A，只有两种可能。出生和不出生，故符合二项式分布X~b(n,p)。
故其出生率\({P \left( X=x \left| \theta \left) =C\mathop{{}}\nolimits_{{n}}^{{x}} \theta \mathop{{}}\nolimits^{{x}} \left( 1- \theta \left) \mathop{{}}\nolimits^{{n-x}},x=0,1,...,n\right. \right. \right. \right. \right. }\)
这就是似然函数，A事件发生下的概率。
如果是严格的似然函数，应转换成向量的分布。
\({P \left( \overline {X} \left| \theta \left) ={\mathop{ \prod }\limits_{{i=1}}^{{n}}{P \left( x=x\mathop{{}}\nolimits_{{i}} \left| \theta \right) \right. }}\right. \right. \right. }\)
第二步：先验条件
如果确定先验条件，这里有一项原则可以利用。假如对某个事件一无所知时，可以先假设事件在某个区间内是均匀分布（即贝叶斯假设原理:即同等无知的原则，认知是一样的）。按这个假设条件，得到θ的先验分布函数。
\({ \pi \left( \theta \left) { \left\{ \begin{array}{*{20}{l}} {1,0 \le \theta \le 1;}\\ {0,other;} \end{array}\right. }\right. \right. }\)

第三步：对似然函数与先验发布函数进行乘积，得到联合密度函数。
\({h \left( x, \theta \left) =C\mathop{{}}\nolimits_{{n}}^{{x}} \theta \mathop{{}}\nolimits^{{x}} \left( 1- \theta \left) \mathop{{}}\nolimits^{{n-x}},0 \le \theta \le 1\right. \right. \right. \right. }\)
看到上和每一步的似然函数一样，但其意义是不同的。

第四点：求出m(x)边际分布
\({m \left( x \left) ={\mathop{ \int }\limits_{{ \theta }}^{{}}{h \left( x, \theta \left) d \theta \right. \right. }}\right. \right. }\)

第五点：得到后验分布（贝叶斯分布）
\({ \pi \left( \theta \left| x \left) =\frac{{h \left( x, \theta \right) }}{{m \left( x \right) }}=\frac{{P \left( x \left| \theta \left) \pi \left( \theta \right) \right. \right. \right. }}{{{\mathop{ \int }\limits_{{ \theta }}^{{}}{P \left( {x \left| \theta \right. } \right) }}{ \pi \left( \theta \right. }\text{）}d \theta }}\right. \right. \right. }\)
第六点：根据有限样本，代入到后验分布公式中
比如收集数据发现1745至1770年出生，男婴251527，女婴241945女婴。
\({P \left( \theta \le 0.5 \left| x \left) ={\mathop{ \int }\limits_{{0}}^{{0.5}}\begin{array}{*{20}{l}} { \pi \left( dx \left) d \theta =1.15 \times 10\mathop{{}}\nolimits^{{-42}}\right. \right. }\\ {} \end{array}}\right. \right. \right. }\)
θ小于0.5的概率很小，故

\({ \theta > 0.5\text{是}\text{此}\text{结}\text{果}\text{被}\text{证}\text{明}}\)