概率论和数理统计_06_一维随机变量

随机变量X=X（e）是一个单实值函数，随机试验的每个结果都对应一个单值实数。
离散性随机变量:有限个或可列无限个。对于离散型随机变量的分布律：随机变量X取到各个可能值Xk(k=1,2...)的概率P（X=xk)=Pk称为随机变量X的概率分布，Pk称为分布律：

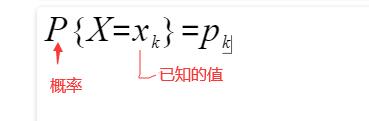
显然概率Pk应满足非负性和全部概率之和为1的特性，即
即所有的pi大于0，\({p\mathop{{\mathop{{}}\nolimits_{{i}}}}\nolimits_{{}} \ge 0,i=1,2,3...}\)
所有的概率总合为1.
\({{\mathop{ \sum }\limits_{{i=1}}^{{ \infty }}{p\mathop{{}}\nolimits_{{i}}=1}}.}\)

常用的离散型随机变量

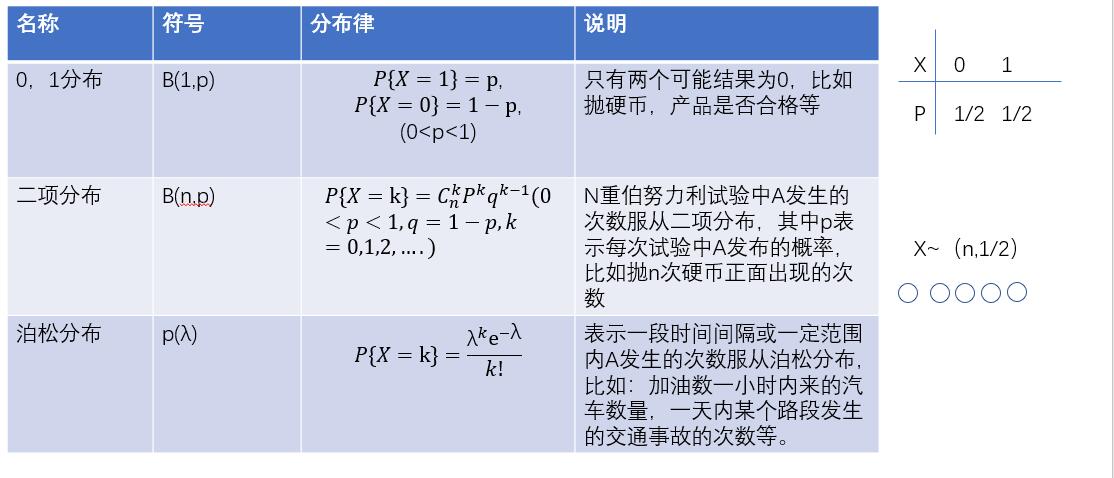
泊松定理*
设X服从二项分布B（n,p），当n较大，p较小时，X近似服从泊松分布P（np）,即

\({P \left\{ X=k \left\} =C\mathop{{}}\nolimits_{{k}}^{{n}}P\mathop{{}}\nolimits^{{k}}q\mathop{{}}\nolimits^{{1-k}} \approx \frac{{ \left( np \left) \mathop{{}}\nolimits^{{k}}e\mathop{{}}\nolimits^{{-np}}\right. \right. }}{{k!}}\right. \right. }\)

离散随机变量分布函数
设X是一个随机变量，x是任意实数，函数
\({F \left( x \left) =P \left\{ X \le x \left\} , \left( - \infty < x < + \infty \right) \right. \right. \right. \right. }\)
随机变量的概率=随机变量大X小于或等于某个小X的概率。其实分布函数是一个累积函数。

显然分布函数F(x)具有以下基本性质;
1.F(x)是一个不减函数，随x的增大逐渐累积
2. \({P \left( a < X \le b \left) =F \left( a \left) -F \left( b \right) \right. \right. \right. \right. }\) 如果大F函数是已知的，则能计算范围中的概率
3.\({0 \le F \left( x \left) \le 1\text{，}F \left( - \infty = \left) 0\text{，}F \left( + \infty \left) =1\right. \right. \right. \right. \right. \right. }\) 样本空间为负无穷，故其累积概率为0，样本空间为正无穷，故其累积概率为1.即所有的样本空间都包含了。
4.根据第三点，F(x)是右连续的
例：设随机变量X的分布律为:

1)求常数a, 2)X的分布函数F(x) ，并画出F(x)图像
解：1） a=1-0.5-0.2=0.3,因为累积概率为1
2）
\(\begin{array}{*{20}{l}}{F \left( x \left) =P \left( X \le x \right) \right. \right. }\\{}\end{array}\)

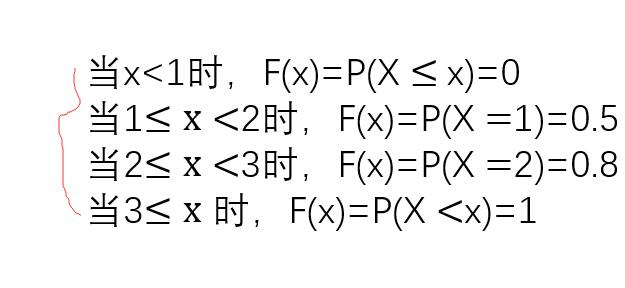
\(\begin{array}{*{20}{l}} {}\\ {F \left( x \left) ={ \left\{ \begin{array}{*{20}{l}} {0\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }x < 1}\\ {0.5\text{ }\text{ }\text{ }\text{ }1 \le x < 2}\\ {0.8\text{ }\text{ }\text{ }2 \le x < 3}\\ {1\text{ }\text{ }\text{ }\text{ }x \ge 3} \end{array}\right. }\right. \right. } \end{array}\)

所以可以看到累积函数F(x)右连续，且是个不减的函数。

连续性随机变量：