概率论和数理统计_05_独立性
-
如果A,B是两事件,满足等式
\({P \left( AB \left) =P \left( B \left| A \left) P \left( A \left) =P \left( A \left) P \left( B \right) \right. \right. \right. \right. \right. \right. \right. \right. \right. }\)
则称事件A,B是相互独立,简称A,B独立 -
独立重复试验
将某试验独立重复n次,若每次实施中事件A发生的概率为p,则n次试验中A发生的k次的概率为:\({P \left( X=k \left) =C\mathop{{}}\nolimits_{{n}}^{{k}}p\mathop{{}}\nolimits^{{k}} \left( 1-p \left) \mathop{{}}\nolimits^{{n-k}}\right. \right. \right. \right. }\)
例子:某系统由四个部件Ⅰ,Ⅱ,Ⅲ,Ⅳ构成,且四个部件是相互独立的,求整个系统的可靠性。
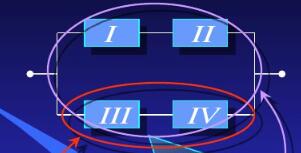
解:记 A={整个系统正常工作}
Ai={某个部件正常工作}
\({P \left( A\mathop{{}}\nolimits_{{1}}A\mathop{{}}\nolimits_{{2}} \left) +P \left( A\mathop{{}}\nolimits_{{3}}A\mathop{{}}\nolimits_{{4}} \left) -P \left( A\mathop{{}}\nolimits_{{1}}A\mathop{{}}\nolimits_{{2}} \cap A\mathop{{}}\nolimits_{{3}}A\mathop{{}}\nolimits_{{4}} \right) \right. \right. \right. \right. }\)

\({=P\mathop{{}}\nolimits^{{2}}+P\mathop{{}}\nolimits^{{2}}-P\mathop{{}}\nolimits^{{2}}P\mathop{{}}\nolimits^{{2}}}\)
例2:设每个人血清中含有肝炎病毒的概率为0.4%,求混合100个人的血清中含有肝炎病毒的概率。
设 A={血清中含有肝炎病毒} 则P(A)=0.4%,则P{不含有肝炎病毒的}=99.6%
P(A)=1-P{不含有肝炎病毒的}
\({=1-P \left( \mathop{{ \cap }}\limits_{{i=1}}^{{100}} \left) \overline {A}\mathop{{}}\nolimits_{{i}}\right. \right. }\)
\({=1-0.996\mathop{{}}\nolimits^{{100}}}\)




