概率论和数理统计_04_条件概率
例如:一个班共有100个学生,其中高数挂科30%,线代挂科25%,那么高数挂科的同学,代数挂科的概率是多少?(注意:与高数与代数同时挂科的概率是多少是有区别的,区别在于,一个是整个班的同时挂科率,即样本空间是整个班100名同学,而题目中的样本空间是高数挂科的)
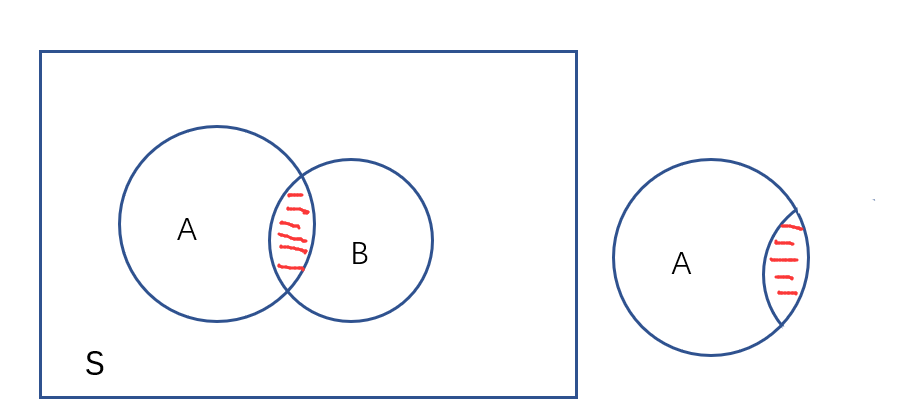
总样本空间为:s=100
A事件的概率:高数挂科概率=30%
B事件的概率:线代挂科概率=25%
在A挂科的情况下,B事件的概率即为条件概率 P(B|A)=
\({P \left( B \left| A \left) =\frac{{P \left( AB \right) }}{{P \left( A \right) }}\right. \right. \right. }\)
即A与B的交集除以A的样本点空间。
例子:设一盒球里面有6个红的,4个白的。不放回抽取,每次任取一个,共取两次。
1)已知第一次取到白球,求第二次取到红球的概率。
2)求第一次取到白球,第二次取到红球的概率。
假设A事件为取到红球,”取到红球“第一次为A1,第二次抽球为A2。A的对应事件则为”取到白球“
题1中第一次取到红球,则剩下9个球,在9个中取红球的概率,即:
\([{P \left( \text{ }A\mathop{{}}\nolimits_{{2}} \left| \overline {A}\mathop{{}}\nolimits_{{1}} \left) =\frac{{6}}{{9}}=\frac{{2}}{{3}}\right. \right. \right. }\)
题2与题1的区别是:题1出现了”已知',说明是条件。题2则是普通的分步计算法计算。
\({\begin{array}{*{20}{l}}
{P \left( \text{ } \overline {A}\mathop{{}}\nolimits_{{1}}A\mathop{{}}\nolimits_{{2}} \left) =P \left( \text{ } \overline {A}\mathop{{}}\nolimits_{{1}} \left) \times P \left( \text{ }A\mathop{{}}\nolimits_{{2}} \left| \overline {A}\mathop{{}}\nolimits_{{1}} \left) =\frac{{4}}{{10}} \times \frac{{2}}{{3}}=\frac{{4}}{{15}}\right. \right. \right. \right. \right. \right. \right. }\\
{\text{ }\text{ }\text{ }}
\end{array}}\)
例2:假设有3张彩票,其中只有1张是中奖奖券,现有3名同学依次无放回地抽取,问最后一名同学中奖的概率是否比其他同学小。
设X=没中奖 ,y=中奖
样本空间s={yxx,xyx,xxy},只有三种情况。最后一名中奖的概率也是1/3
但已知第1位同学没有中奖,则剩下的样本空间是2,这个时候最后一名中奖的概率就是1/2了
条件概率的性质
1)非负性:对于每一事件B,有P(B|A)>0
2)规范性:对于必然事件s,有P(s|A)=1
3) 可列可加性:设B1,B2...是两两互不相容的事件,则有
\({\begin{array}{*{20}{l}}
{P \left( \mathop{{\mathop{{ \cup }}\limits^{{ \infty }}}}\limits_{{i=1}}^{{}}B\mathop{{}}\nolimits_{{i}} \left| A \left) ={\mathop{ \sum }\limits_{{i=1}}^{{ \infty }}{P \left( B\mathop{{}}\nolimits_{{i}} \left| A \right) \right. }}\right. \right. \right. }\\
{\text{ }\text{ }\text{ }}
\end{array}}\)
和事件发生的总概率=条件下的所有和事件发生概率的和。
乘法公式
\({\begin{array}{*{20}{l}}
{P \left( AB \left) =P \left( B \left| A \left) \times P \left( A \right) \right. \right. \right. \right. \right. }\\
{\text{ }\text{ }\text{ }}
\end{array}}\)
可以理解为AB同时发生的概率=条件A发生的情况下B发生的概率*A在整个样本空间发生的概率。
上式可推广到多个事件的积事件的情况。例如:设A,B,C为事件,且P(AB)>0,则有P(ABC)=P(C|AB)P(B|A)P(A)
\({\begin{array}{*{20}{l}}
{P \left( AB \left) =P \left( B \left| A \left) \times P \left( A \right) \right. \right. \right. \right. \right. }\\
{P \left( B \left) =0.4,P \left( A+B \left) =0.5,\text{求}\text{ }P \left( A \left| \overline {B} \left) \text{ }\text{ }\right. \right. \right. \right. \right. \right. \right. }\\
{P \left( A \left) =1-0.5=0.5\right. \right. }\\
{P \left( \overline {B} \left) =1-0.4=0\text{ }.6\right. \right. }\\
{P \left( A \left| \overline {B} \left) =\frac{{P \left( A \overline {B} \right) }}{{P \left( \overline {B} \right) }}=\frac{{0.1}}{{0.6}}=\frac{{1}}{{6}}\right. \right. \right. }\\
{\text{ }}\\
{}
\end{array}}\)

看图可知
\({P \left( A \overline {B} \right) }\)=A与B对立事件的交集,即0.1
第二种办法:公式推导
\({P \left( A \left| \overline {B} \left) =1-P \left( \overline {A} \left| \overline {B} \left) =1-\frac{{1-P \left( A \cup B \right) }}{{1-P \left( B \right) }}=1-\frac{{1-0.5}}{{1-0.4}}=\frac{{1}}{{6}}\right. \right. \right. \right. \right. \right. }\)
例2: 一张储蓄卡的密码共有6位数字,每位数字都可以从0-9中任选一个,某人在银行自动提款机上取钱时,忘记了密码的最后一位数字,求
1)任意按最后一位数字,不超过2次就按对的概率。
设事件按对为A,第一次按对A1,对二次按对A2
不超过2次按对的概率,第一个按对或第二个按对都算是不超过2次按对。
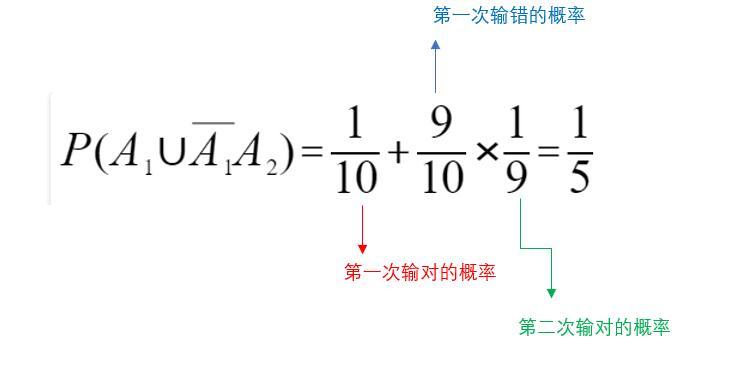
2)如果他记得密码的最后一位是偶数,不超过2次就按对的概率
与上面是一样的,只是样本空间变成了{0,2,4,6,8},共有5个字
\({{P \left( \mathop{{A}}\nolimits_{{1}} \cup \overline {\mathop{{A}}\nolimits_{{1}}}A\mathop{{}}\nolimits_{{2}} \left) =\frac{{1}}{{5}}+\frac{{4}}{{5}} \times \frac{{1}}{{4}}=\frac{{2}}{{5}}\right. \right. }}\)
例3:某班级课程的不及格率为4%,而及格同学中将有25%的同学可以等到A,求该同学得到A的概率。
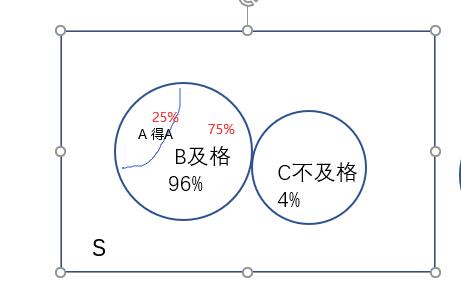
事件A:得A,事件B:及格
已知:
\({\begin{array}{*{20}{l}}
{A \subset B,AB=A,P \left( AB \left) =P \left( A \right) \right. \right. }\\
{P \left( B \left) =1-4\text{%}=96\text{%}\right. \right. }\\
{P \left( A \left| B \left) =25\text{%}\right. \right. \right. }\\
{P \left( AB \left) =P \left( B \left) \times P \left( A \left| B \left) =96\text{%} \times 25\text{%}=0.24\right. \right. \right. \right. \right. \right. \right. }
\end{array}}\)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号