概率论和数理统计_03_古典概型和几何概型

古典概型

特点：
1）试验的样本空间只包含有限个元素。
2）实验中每个基本事件发生的可能性相同

计算公式:
\({P \left( A \left) =\frac{{A\text{包}\text{含}\text{的}\text{基}\text{本}\text{事}\text{件}\text{数}n \left( A \right) }}{{S\text{中}\text{基}\text{本}\text{事}\text{件}\text{的}\text{总}\text{数}n}}\right. \right. }\)

例子1：（生日问题）假设每人的生日在一年365天中任意一天是等可能的，求下列事件发生的概率：
1）事件A={3个人生日不同的概率}
假定第一个人在365天中选了一天，那么第二个人就不能再选这一天了，即只要364天中选一天。
\({P \left( A \left) =\frac{{\text{ }C\mathop{{}}\nolimits_{{365}}^{{1}} \times \text{ }C\mathop{{}}\nolimits_{{364}}^{{1}}\text{ }C\mathop{{}}\nolimits_{{363}}^{{1}}}}{{365 \times 365 \times 365}}\right. \right. }\)
也可以写成:
\({P \left( A \left) =\frac{{\text{ }365 \times 364 \times 363}}{{365 \times 365 \times 365}}\right. \right. }\)

2）事件B={在30人的班级中，至少有两人生日相同的概率}
通常遇到“至少”字眼，则考虑此事件的对立事件去计算会比较合适。题中的“至少两人生日相同的概率”其对应事件为“所有人的生日不一样”。
同样的道理：假定第一个人在365天中选了一天，那么第二个人就不能再选这一天了，即只要364天中选一天....即
\({P \left( B \left) =1-\frac{{\text{ }\mathop{\mathop{{365 \times 364 \times 363∙∙∙∙336}}\limits^{︷}}\limits^{{30}}}}{{365\mathop{{}}\nolimits^{{30}}}}\right. \right. }\)

例子2: 从5双不同的鞋子中任取4只，求其中至少两只配成一双。
样本空间：5双，即10只鞋中选出4只。
事件中：又出现了“至少'两字，所以对立事件是”四只鞋没有一只是相同的“。首先将10只鞋当成5双鞋，即”捆绑法“，先从5双鞋中找到四双鞋，再从每双鞋中抽一只，，即能实现”四只都不能配成一双“的事件。
抽象--具体
\({P \left( B \left) =1-\frac{{C\mathop{{}}\nolimits_{{5}}^{{4\text{ }}}C\mathop{{}}\nolimits_{{2}}^{{1\text{ }}}C\mathop{{}}\nolimits_{{2}}^{{1\text{ }}}C\mathop{{}}\nolimits_{{2}}^{{1\text{ }}}C\mathop{{}}\nolimits_{{2}}^{{1\text{ }}}}}{{C\mathop{{}}\nolimits_{{10}}^{{4}}\mathop{{}}\nolimits^{{}}}}\right. \right. }\)
例3：设10个运行队平均分成两组，求最强的两支队伍分在同一组的概率。

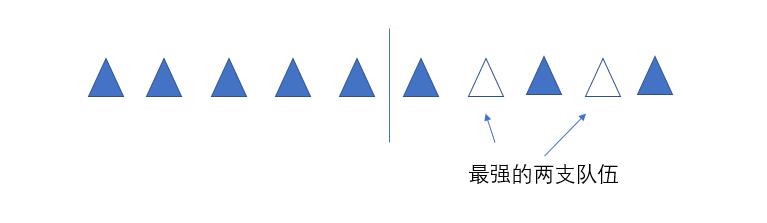
样本空间：10队选出5个运动队组织两支队伍
事件分析：先将两个队进行划分，假设最强的两支队伍选在了一组，则有三个供其他8支队伍随机选，即
\({P \left( A \left) =\frac{{C\mathop{{}}\nolimits_{{2}}^{{1}}C\mathop{{}}\nolimits_{{8}}^{{3}}}}{{C\mathop{{}}\nolimits_{{10}}^{{5}}}}\right. \right. }\)

例子4： 设一个袋中有7个球，4个白球，3个黑球，求下列试题：
从中一次性取4个球，求恰好取到3个白球的概率。

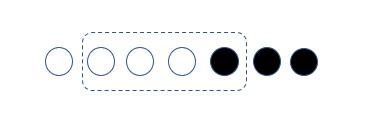
样本空间：7个球选4个球
事件:假设要做到取4个球有3个白球的概率，也就是4个白球选3个白球，3个黑球选1个黑球的事件。
\({P \left( A \left) =\frac{{C\mathop{{}}\nolimits_{{4}}^{{3\text{ }}}C\mathop{{}}\nolimits_{{3}}^{{1\text{ }}}}}{{C\mathop{{}}\nolimits_{{7}}^{{4}}\mathop{{}}\nolimits^{{}}}}\right. \right. }\)

此例推广：N件产品，N1次产品，从中取出n件，问取出n1件次品的概率。

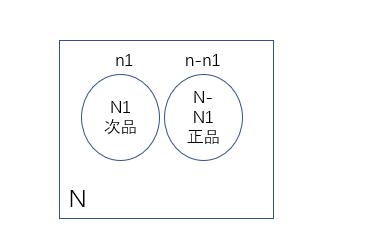
样本空间：N件产品取n件
事件:在次品N1空间中，取n1个次品，在正品N-N1空间中，取n-n1正品
\({P \left( A \left) =\frac{{C\mathop{{}}\nolimits_{{N1}}^{{n1\text{ }}}C\mathop{{}}\nolimits_{{N-N1\text{ }}}^{{n-n1}}}}{{C\mathop{{}}\nolimits_{{N}}^{{n}}\mathop{{}}\nolimits^{{}}}}\right. \right. }\)
此公式就是”超几何概型公式“。
上例第2问：有放回地抽取4个球，求恰好取到3个白球的概率。
放回抽样，每次抽的概率是不变的。按分步法做乘积：
但还要考虑每次抽的虽然3个白球一个黑球，但位置会不一样。即可能前面3个白球，后面1个黑球，前面一个黑球，后面三个白球等。故我们先把7个位置，抽四个位置给到放置球，再考虑球的每次抽回概率。

\({P \left( B \left) =C\mathop{{}}\nolimits_{{4}}^{{3}}\frac{{4}}{{7}} \times \frac{{4}}{{7}} \times \frac{{4}}{{7}} \times \frac{{3}}{{7}}\right. \right. }\)
这个就是”n次伯努利试验“。
1）n次独立重复
2）每次只有两个结果。
计算公式：
\({\begin{array}{*{20}{l}} {P \left( A \left) =p,P \left( \overline {A} \left) =1-p=q\right. \right. \right. \right. }\\ {P \left( A\text{发}\text{生}k\text{次} \left) =C\mathop{{}}\nolimits_{{k}}^{{n}}p\mathop{{}}\nolimits^{\begin{array}{*{20}{l}} {k\text{ }\text{ }}\\ {} \end{array}}q\mathop{{}}\nolimits^{{\begin{array}{*{20}{l}} {n-k\text{ }\text{ }}\\ {} \end{array}}}\right. \right. } \end{array}}\)

k表示事件的发生的次数，上例的抽到白球的个数，q表是事件的对立事件，上例抽到黑球的事件。

几何概型

上面的古典概型对样本空间有要求是有限个的。但很多时候随机试验的事件个数不是有限个而是无穷多个时。当试验的样本空间可用某个区域G来表示，并且任意多一点落在该区域内度量相同的子区域是等可能的，则事件A发生的概率为\({P \left( A \left) =\frac{{m \left( G\mathop{{}}\nolimits_{{A}} \right) }}{{m \left( G \right) }}\right. \right. }\)
上面的文字有点抽象，举个例子说明。
假设 在0至100中投一个数的可能性。这个数落在0-10之间、50-60之间的可能性，只要这个区间长度是一样的，则落的概率也是相同。而概率=区间的长度/总长度。拓展到二维空间，则是指样本空间的面积比例。拓展到三维空间，则指样本空间的体积比例。

例如：甲、乙两人约好在下午4:00-5:00间在某地相见，他们约好当其中一人先到后一定要等到另一人15分钟，若另一人仍不到，则可以离去，试求这两个人能相见的概率。
该问题可以理解为：两个对象的时间差。
设:x=甲到达的时间
y=乙到达的时间
此问题可以理解为 |x-y|<=15分钟。
按60分钟画图来显示|x-y|<15分钟的面积，下图画色部分即为两者到达时间差为15分钟的面积。

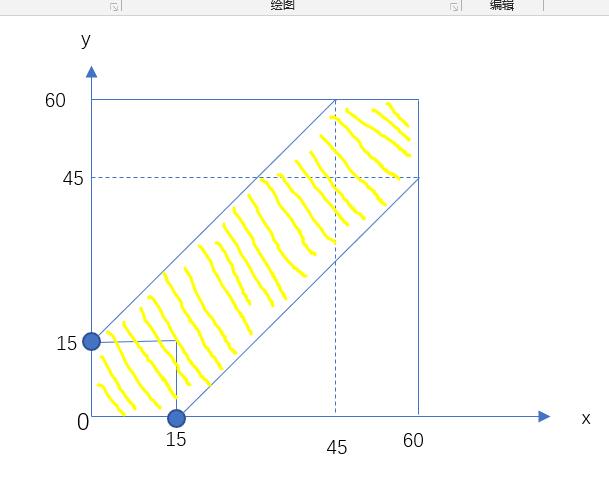
故此概率为黄色阴影面积：
\({P \left( A \left) =\frac{{60 \times 60-45 \times 45}}{{60 \times 60}}\right. \right. }\)