概率论和数理统计_01_排列组合

引言
“概率论和数理统计”是为了对事物进行预测，就类似于算命。算命需要事行知道命运的所有可能性，这就是前提。那如何知道某项事件的所有可能性呢，这里引入高中所学知识“组合排列”。

组合：\({C\mathop{{}}\nolimits_{{48}}^{{4}}=\frac{{48 \times 47 \times 46 \times 45}}{{4 \times 3 \times 2 \times 1}}}\) n个元素中选出m个元素组合
排列：\({A\mathop{{}}\nolimits_{{48}}^{{4}}=48 \times 47 \times 46 \times 45}\) n个元素中选出m个元素进行排序

排列组合两个重要的计算方法
一、分类计数法
比如：从A城市到B城市，可以坐飞机、动车、骑自行车。假如飞机有一个航班，动车有三个车次，自行车可以骑小黄车、mobile即两种方法。

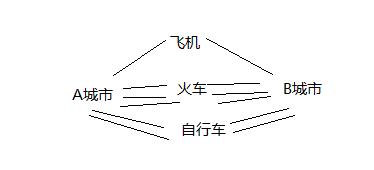
1+3+2=6,总共有6种方法可以到B城市。

分类计数法，也称“加法原理”

二、分步计数法
比如：从A城市到B城市，必须经过C城市。A到C有三条路线，C到B有两条线路，则共有3*2=6，共6种方法

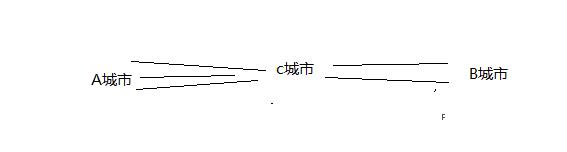
分步计数法，也叫“乘法原理”

例1：6名同学排成一排，其中甲、乙两个必须排在一起的不同排法有（）种。
“捆绑法”，即将甲、乙当成一个整体，看成一个人。与剩下的四名同学进行排列，先排列5人，再对甲、乙进行排列。
\({{A\mathop{{}}\nolimits_{{5}}^{{5\text{ }\text{ }\text{ }\text{ }}} \times \text{ }A\mathop{{}}\nolimits_{{2}}^{{2\text{ }\text{ }\text{ }\text{ }}}}}\)

例2： 要排一张有6个歌曲和4个舞蹈节目的演出节目单，任意两个舞蹈节目不得相邻，有多少种不同的排法？
抽象---转“形象”

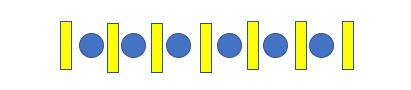
将歌曲看成蓝色的球，黄色的部分即放演示节目即可实现不相邻的位置，观察黄色条共有7个，也就是四个节目按不同排序放到此7个黄色条即可实现任意两个舞蹈节目不得相邻。因为6个节目本身也有排序，故答案如下：
\({{A\mathop{{}}\nolimits_{{6}}^{{6\text{ }\text{ }\text{ }\text{ }}}A\mathop{{}}\nolimits_{{7}}^{{4\text{ }\text{ }\text{ }\text{ }}}}}\)

这里用的方法叫“插空法”，与上面的“捆绑法”解决的场景不一样的是：捆绑法是要在一起，插空法是要解决不在一起。

例3： 将8个完全相同的球放进3个不同的盒子中，要求每个盒子至少有一个球，一共有多少种放法？
抽象--转“形象”
如果要实现每个盒子至少有一个球，可以采用“插板法“，将此问题转换成：用两个板子隔开，即8个球分成三份。故该问题成了解决两个板子放的位置。

放板子的位置共有7个空位，将两个板子放到这七个位置中，才能保证每一份至少有一个球。因为8个球完成一样，故没有涉及球的排列。这个题就是7个空隔中选2个
\({{C\mathop{{}}\nolimits_{{7}}^{{2\text{ }\text{ }\text{ }\text{ }}}}}\)

例4：有甲、乙、丙三项任务，甲需由2个人承担，乙丙各需一个人承担，从10个人选出4个人承担这三项任务，不同的选法（）种

第一种方法：从10个人选出4个人，从这4个人中选择2个人承接甲，剩下2人。从这2人中选择一位接乙任务，剩下一人只能接丙任务了。注意多个人接一项任务是不有排序的。
\({{C\mathop{{}}\nolimits_{{10\text{ }}}^{{4\text{ }\text{ }\text{ }\text{ }}}C\mathop{{}}\nolimits_{{4}}^{{2\text{ }\text{ }\text{ }\text{ }}}C\mathop{{}}\nolimits_{{2}}^{{1\text{ }\text{ }\text{ }\text{ }}}C\mathop{{}}\nolimits_{{1}}^{{1\text{ }\text{ }\text{ }\text{ }}}}}\)

第二种方法：选从10个中选2个人承担甲任务，剩下8个人，再从这8个人中选择1个人承接乙，剩下7个人再选1个承接丙
\({{C\mathop{{}}\nolimits_{{10\text{ }}}^{{2\text{ }\text{ }\text{ }\text{ }}}C\mathop{{}}\nolimits_{{8}}^{{1\text{ }\text{ }\text{ }\text{ }}}C\mathop{{}}\nolimits_{{7}}^{{1\text{ }\text{ }\text{ }\text{ }}}}}\)

例5：由数字0，1，2，3，4，5组成没有重复数字的六位数，其中个位数小于十位数的共有（）个
第一种方法：分类法

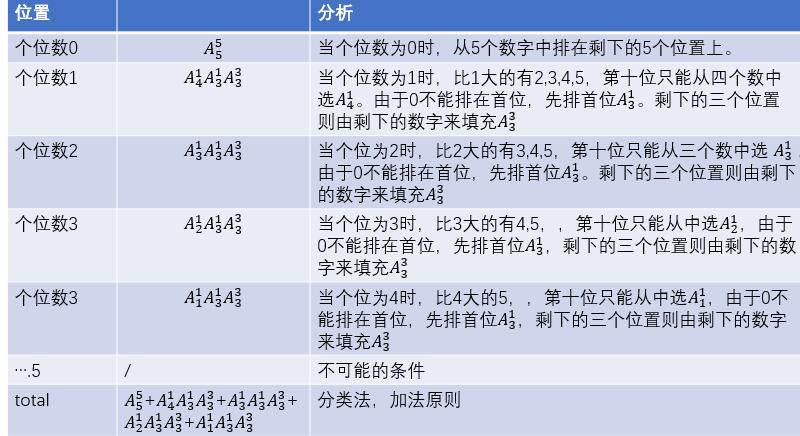
看上去很复杂，而且计算不便，建议采用第二种分步计算法
即然首位不可以为0，先排首位，再排个位和十位。（随便选两个数，肯定有一个大有一个小，不要用排列，用组合即可实现），最后剩3个数，全排列。

第二种方法计算起来更简单且不容易出现遗漏，但要灵活利于组合这一项特点。

例6：四个不同的小球放入编号1，2，3，4的四个盒子中，则恰有一个空盒的放法共有（）种
抽象---转”形象“
如果要实现恰好有一个空盒，则必然有一个盒子装两个，有两盒子各装一个。见下图:

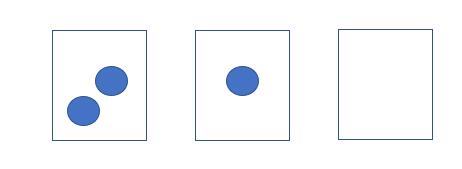
由于球不同，盒子不同。我们先将球排列入盒子中，先取2个看成一个整体，再四个盒子中任意选择三个盒子装
\({{C\mathop{{}}\nolimits_{{4\text{ }}}^{{2\text{ }\text{ }\text{ }\text{ }}}A\mathop{{}}\nolimits_{{4}}^{{3\text{ }\text{ }\text{ }}}}}\)
先”捆绑“，因为放在一个盒子里的两个球是不需要顺序的。