用实例并可视化去理解拉格朗日对偶函数的凹性质
考虑约束最优化问题：
\[\begin{aligned}
&min &&f(x) \\
&s.t. &&c_i(x)\leq 0, i=1,2,...,l,\\
&&&h_i(x) = 0,i=l+1,l+2,...,n
\end{aligned}
\]
拉格朗日化后为：
\[\begin{aligned}
&\Delta L(x,\vec{\lambda}) = \Delta L(x,\lambda_1,\lambda_2,\cdots,\lambda_n) = \Delta(f(x,y)+\sum_{i=1}^{l}\lambda_i c_i(x)+\sum_{i=l+1}^{n}\lambda_i h_i(x)) = 0,\\
&s.t. \forall i \in \{1,2,...,l\}, \lambda_i \geq 0
\end{aligned}
\]
该拉格朗日函数为：
\[L(x,\vec{\lambda})=f(x)+\sum_{i=1}^{l}\lambda_i c_i(x)+\sum_{i=l+1}^{n}\lambda_i h_i(x),\forall i \in \{1,2,...,l\}, \lambda_i \geq 0
\]
因为\(\forall i \in \{1,2,\cdots,l\}\),\(c_i(x) \leq 0,\lambda_i \geq 0;\forall i \in \{l+1,l+2,\cdots,n\}\),\(h_i(x) = 0\)，所以：
\[L(x,\vec{\lambda}) = f(x)+\sum_{i=1}^{l}\lambda_i c_i(x)+\sum_{i=l+1}^{n}\lambda_i h_i(x) \leq f(x)
\]
就是说：对任意的\(x\)，
那么，
则有：
\[min(L(x,\vec{\lambda})) \leq min(f(x))
\]
于是，我们把拉格朗日的对偶函数定义为：
$$
g(\vec{\lambda}) = min(L(x,\vec{\lambda})) = min(f(x)+\sum_{i=1}^{l}\lambda_i c_i(x)+\sum_{i=l+1}^{n}\lambda_i h_i(x))
$$
函数$g$的意义为：现在，让我们看看拉格朗日对偶函数的凹性质：
函数$g(\vec{\lambda})$可以写成如下形式： $$ \begin{aligned} g(\vec{\lambda}) &= min(f(x)+\sum_{i=1}^{l}\lambda_i c_i(x)+\sum_{i=l+1}^{n}\lambda_i h_i(x))\\ &=min(f(x)+\left[\begin{matrix} c_1(x)&c_2(x)&\cdots&c_l(x)&h_{l+1}(x)&h_{l+2}(x)&\cdots&h_n(x) \end{matrix} \right] · \left[\begin{matrix} \lambda_1&\lambda_2&\cdots&\lambda_n \end{matrix} \right]) \end{aligned} $$ 其中， $$ \begin{aligned} &f(x) \in R,\\ &\forall i \in \{1,2,\cdots,l\},c_i(x) \leq R,\\ &\forall i \in \{l+1,l+2,\cdots,n\},h_i(x) = 0 \end{aligned} $$ 就是说，$k(\vec{\lambda})= \left[\begin{matrix} \vec{c(x)};\vec{h(x)}\end{matrix} \right] · \vec{\lambda}$是一个超平面(类似于$2 · x$，前面的‘；’表示拼接两个向量)，$ \left[\begin{matrix} \vec{c(x)};\vec{h(x)}\end{matrix} \right]$就是一个超平面的系数。那么说明：
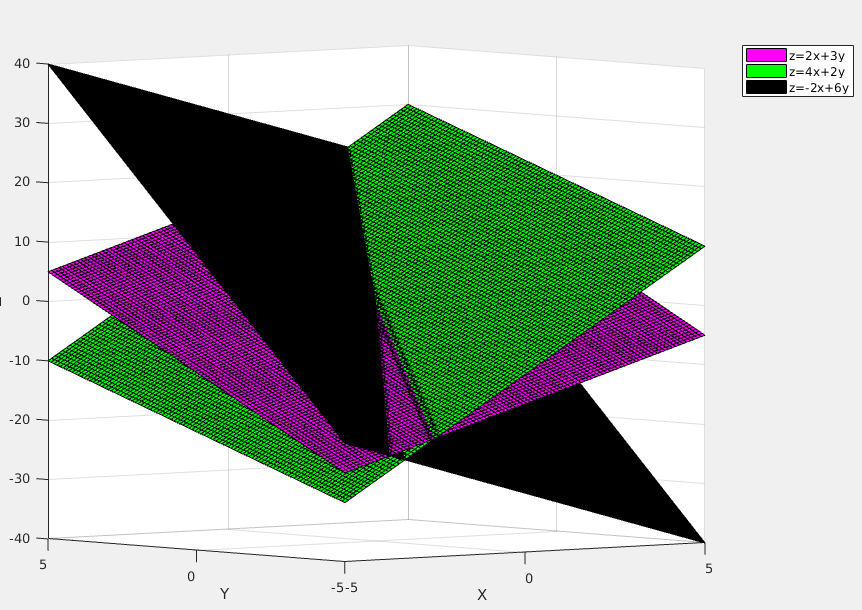
三维空间中的几个‘超平面’
|
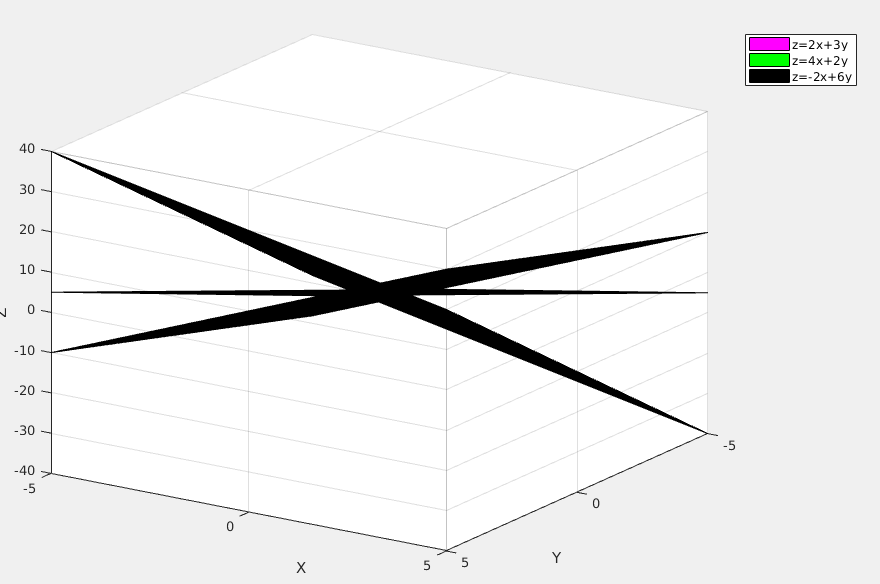
左图在点（-5-5）处往上掰看的视图
|
从图中可以看到，不同的超平面相交后，如果我们对于一个\(\vec{\lambda}\)，取，使函数\(k(\vec{\lambda})\)，最小的值，那么可以看到：
x = linspace(-5,5,100);
y = linspace(-5,5,100);
[x,y]=meshgrid(x,y);
z1 = x.*2+y.*3;
z2 = x.*4+y.*2;
z3 = x.*(-2)+y.*6;
z4 = x.*(-3)+y.*(-3);
surf(x,y,z1);hold on;surf(x,y,z2);hold on;surf(x,y,z3);surf(x,y,z4);
hold on; legend('z=2x+3y','z=4x+2y','z=-2x+6y','z=-3x-3y');
参考文献：
如何理解拉格朗日对偶函数_PandaRELEASE的博客(上图的工作源自此文章的对对偶函数的解释）
凸优化中的对偶问题与共轭函数（对对偶函数的定义来自此文）
