低副瓣阵列天线综合4 matlab HFSS

这一篇就接着研究串馈的两种形式下已知电流比后如何计算导纳或阻抗，从而计算出仿真需要的模型宽度初始值。

一种是通过改变振元宽度来达到电流加权的，

另外一种是通过1/4阻抗变换段实现电流加权的，一般多用在面阵的功率分配上，

 

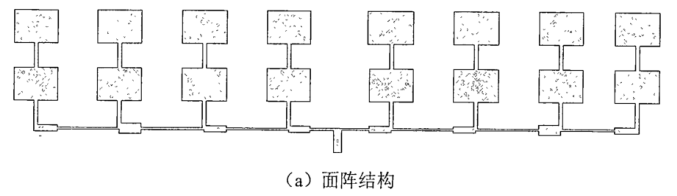
 第一种加权的实现是通过导纳比为电流的平方比来计算的，归一化后，左右对称的第一个振元的辐射电导最大归一为1，

第一个振元的宽度可以用微带矩形振子的相关公式计算，再根据下面的计算公式计算电导值：

 

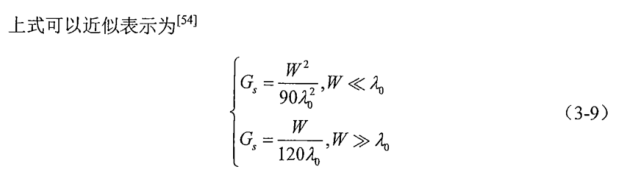
其它振元与这第一个振元电导之间的关系是如下：

 

 

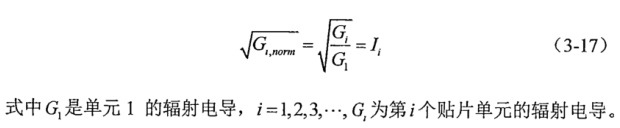
下面举个例子，假设我们已经根据副瓣抑制的要求通过matlab计算出来所需的电流分布归一化如下：

I1:I2:I3:I4=1:0.8424:0.5843:0.3778       如果W1=4.07mm  lamda0=12.422mm

先由3-9式计算得G1=0.00119317   ；G2=I2^2*G1 =0.00084672    W2= 3.43mm；依次类推分别计算出

各振元的宽度W3=2.38mm W4=1.54mm； 但是查了很多论文都没有这篇讲的清楚，有些论文直接拿电流平方比

来进行阻抗比的计算，让我也很有点迷惑，如果按照阻抗比等于电流比，那W2=2.89mm，差距还是比较大的；

第二种1/4阻抗变换段的计算过程:

设阻抗变换段的导纳比ni=y0/yi=zi/z0   其中y0 z0是馈线的 yi zi是阻抗变换段的；然后又开始了烦人的递推，

yin=y1=y0+(n1^2)*y2=y0+(n1^2)*(y0+(n2^2)*y3).......最后yn=1，所以yin=y0*(1+n1^2+n1^2*n2^2+...+n1^2*n2^2...Nn-1^2)

所以电流分布由ni决定，第一个单元的激励电流归一，I1=y0V=1,I2=n1*y0V=n1，I3=n2*I2=n2*n1;

例如电流分布为1：0.7267：0.3865，那么0.7267=n1=z2/z0，如果选z0=100ohm，那么z2=72.67ohm；z1的值是用来匹配整个

一端的匹配的。

到这里做串馈微带天线面阵就都搞完了，后面就是在HFSS里面建模仿真优化了。