局部多项式插值法的工作原理
===================================================================
全局多项式插值法可以根据整个表面拟合多项式，而局部多项式插值法可以对位于指定重叠邻域内的多个多项式进行拟合。通过使用大小和形状、邻域数量和部分配置，可以对搜索邻域进行定义。或者，可以使用探索性趋势面分析滑块同步更改带宽、空间条件数（如果已启用）和搜索邻域值。还可以通过优化按钮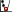 
基于交叉验证统计信息为 LPI 进行参数优化。
一阶全局多项式可以根据数据对单平面进行拟合；二阶全局多项式可以对包含一个弯曲的表面进行拟合（表面可以表示山谷）；三阶全局多项可以对包含两个弯曲的表面进行拟合；依此类推。但是，当表面具有多种形状时（如延绵起伏的地表），单个全局多项式将无法很好地拟合。多个多项式平面能够更加准确地体现表面（参见下图）。
另一方面，局部多项式插值法仅使用既定邻域内的点对指定阶数（0 阶、1 阶、2 阶、3 阶，等等）的多项式进行拟合。邻域相互重叠，每次预测所使用值是位于邻域中心的拟合的多项式的值。
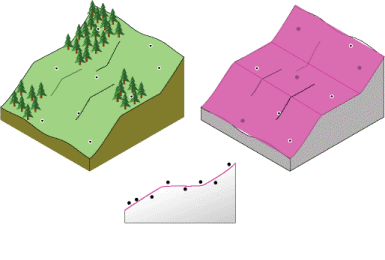
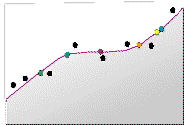
在下图中，截取了样本高程数据的横截面（样带）。在第一幅图中，使用三个相邻点（红色点）对一阶多项式进行拟合，使用一条线（红色线）预测由蓝色点标识的位置所对应的未知值。在第二幅图中，通过另一个一阶段多项式对另一个位置（黄色点）进行预测。由于此位置与第一个位置之间的距离很小，因此在预测过程中使用了相同的测量点，但权重稍有不同，从而使得多项式的拟合效果存在些许差异（蓝线）。
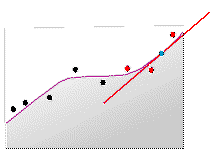
随着这一过程的继续，将侧重于后续的预测位置，拟合局部多项式以对值进行预测。以下两幅图显示了为创建最终表面而被预测的另外两个任意点。橙色点是使用经测量的绿色采样点根据拟合的多项式（绿色线）预测而来的，而褐色点是根据浅紫色多项式预测而来的。
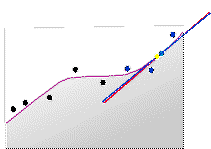
在以下两幅图中，为预测另外两个位置（蓝绿色点和绿色点）对另外两个多项式（黄色线和灰色线）进行了拟合。
将针对各位置重复执行上述过程。您可以看到如何为以下采样点创建表面（紫色表面线）。
与在 IDW 中选择幂 (p) 值相似，也需要在局部多项式中选择最佳参数，以将均方根预测误差 (RMSPE) 降至最小。
准确性的度量
局部多项式插值法提供了两种用于度量准确性的方法，但这两种方法对于 ArcGIS Geostatistical Analyst 中提供的其他确定性插值方法并不适用。
- 预测标准误差用于表示与各位置的预测值相关的不确定性。
- 空间条件数是一种表示预测方程的稳定或不稳定解对特定位置的适应程度的度量方式。如果条件数较大，则很小的矩阵系数变化便会导致解向量（回归系数）的较大变化。由于预测标准误差表面是在假定模型是正确的情况下创建的，因此空间条件数表面可显示数字模型稳定性的变化并提供与预测不确定性相关的其他信息。
局部多项式插值法依赖以下假设：
- 在格网上采样（即，样本的间距相等）。
- 搜索邻域内的数据值呈正态分布。
事实上，大多数数据集都不符合上述假设；在此类情况下，预测值将受到影响，但误差不会像预测标准误差那样大。为帮助确定特定区域内的结果是否可靠，LPI 提供了一个空间条件数表面。下表中显示了一些经验值，这些关键值在“条件数”表面中被渲染成黄色。
多项式的阶
关键空间条件数阈值
1
10
2
100
3
1000
大于 3
大多数情况下都不建议使用
低于关键空间条件数阈值的值表示解在哪个位置可靠。接近或等于关键值的值可能存在问题（应用心检验），高于关键限值的值不可靠。
通过估测当线性预测方程的系数发生微小变化时预测值面对此变化的敏感程度，可以生成空间条件数。如果空间条件数较小，则表示解可靠；如果空间条件数较大，则表示解不可靠。如果解的不稳定性出现在特别感兴趣的区域，则应对此问题格外关注。这是因为，输出数据中（包括数据的值、位置和空间排列）的较小变化会导致预测值发生较大变化。这意味着，与输入数据（例如，属性测量中的误差或进行测量的位置处的坐标不精确）相关的任何不确定性都可能对预测值产生重大影响。此外，搜索邻域的变化会修改在预测中使用的数据点的数量（如果平滑搜索邻域发生变化，还会修改权重）并可能影响位置的空间条件数。
为一阶、二阶和三阶多项式创建空间条件数表面。在假定 LPI 模型正确无误的前提下，估测预测标准误差（即，局部加权最小二乘法回归是合适的算法，并且空间条件数值小于上表中的空间条件数阈值）。
通过在 LPI 对话框中将使用空间条件数阈值设置为 True，可以选择将预测中出现较高条件数的区域和预测标准误差图排除在外。条件数仅与数据位置配置相关。换言之，无论是否将同一个数据集中的臭氧值或高程值用作 LPI 的输入，条件数表面都将保持不变。
如果数据规则分布，那么从理论角度来看，最适用于零阶、一阶和二阶多项式的分别为常数核、Epanechnikov 核和四次核。如果数据不规则分布，则应根据验证和交叉验证诊断以及空间条件数值来选择最佳核。
在含障碍的核插值法中提到的核平滑是 LPI 的一个变型。通过使用类似于岭回归的一种方法对这些结果中的局部不稳定性进行校正。取舍问题指的是预测值存在微小偏差，但在大多数实际情况中，该偏差并不足以对根据预测做出的决定造成影响。
表面中存在“孔洞”。
当使用优化按钮 
时，通常需要更改带宽值、空间条件数和搜索邻域值。如果空间条件数阈值标记被设置为“假”，则只会更改带宽值和邻域值。如果“邻域”类型被设置为“标准”，则会使用所有数据（最多达 1000 个点）并将最小相邻点数设置为 0。将针对等于 1 个分区的“分区”类型以及平滑邻域进行优化。此优化过程可以导致输出表面出现“孔洞”。出现“孔洞”的位置是指超过空间条件数阈值或搜索邻域过小的那些区域。为填平这些区域，可以对搜索邻域参数和空间条件数阈值进行调整。但必须注意到，之所以创建这些“孔洞”，是因为在计算预测值的过程中这些位置可能存在不稳定性。
何时使用局部多项式插值法
全局多项式插值法适用于在数据集中创建平滑表面及标识长期趋势。然而，在地球科学中，除了长期趋势之外，感兴趣的变量通常还具有短程变化。当数据集显示出短程变化时，局部多项式插值法地图可捕获这种变化。
局部多项式插值法对邻域距离很敏感；较小的搜索邻域可能会在预测表面内创建空区域。因此，可以在生成输出图层之前预览表面。
===================================================================
来源：http://resources.arcgis.com/zh-cn/help/main/10.1/index.html#/na/003100000027000000/
评价：应该是从全部多项式插值法进一步的延伸，局部更加精确。关键字是局部！
优点：显著捕获短程变化，
缺点：邻域距离很敏感，较小的搜索邻域可能会在预测表面内创建空区域。空洞现象。
