[蓝桥杯][2019年第十届真题]Fibonacci 数列与黄金分割

题目描述

Fibonacci 数列是非常著名的数列:

F[1] = 1,

F[2] = 1,

对于 i > 3，F[i] = F[i − 1] + F[i − 2]

Fibonacci 数列有一个特殊的性质，前一项与后一项的比值，F[i]/F[i + 1]， 会趋近于黄金分割。

为了验证这一性质，给定正整数 N，请你计算 F[N]/F[N + 1]，并保留 8 位 小数。

输入

一个正整数 N。(1 ≤ N ≤ 2000000000)

输出

F[N]/F[N + 1]。答案保留 8 位小数。

样例输入

2

样例输出

0.50000000

---

思路

这里有一个坑，如果是按照普通的Fibonacci来写的话，会超时。题目说到“会趋近于黄金分割”，于是打印下来输入N=100的情况，可以看到在N=20左右处收敛于0.61803399：

 

 

 

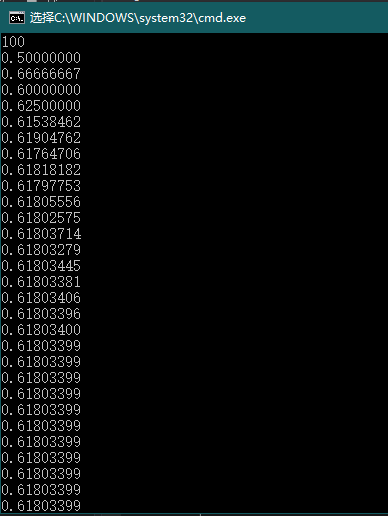
代码

#include<iostream>
#include<iomanip>
using namespace std;
/*

*/

int main()
{
    int n;
    cin >> n;
    int F[20];
    F[0] = 1;
    F[1] = 1;
    for (int i = 2; i<20; i++) {
        F[i] = F[i-1] + F[i-2];
    }
    if (n < 20) {
        double res = double(F[n - 1]) / double(F[n]);
        cout << setiosflags(ios::fixed) << setprecision(8);
        cout << res;
    }
    else
        cout << "0.61803399";
    return 0;
}