多轨车皮编序问题

Description

在一个列车调度站中，k条轨道连接到k条侧轨处，形成k个铁路转轨栈，从左到右依次编号为1，2，…，k。其中左边轨道为车皮入口，编号为0；右边轨道为出口，编号为k+1。当k=2 时，如下图所示。编号为1，2，…，n的n个车皮散乱地停放在编号为0，1，2，…，k的栈轨处。调度室要安排各车皮进出栈次序，使得在出口处各车皮按照其编号次序1，2，…，n依次出站。车皮移动时只能按照从左到右的方向移动。

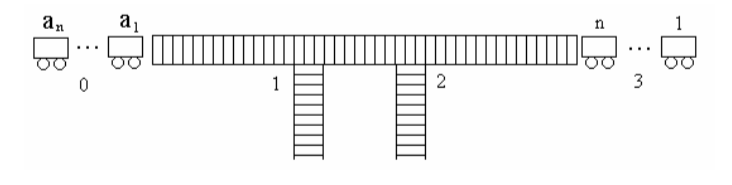
编程任务：给定车皮数n和侧轨数k，以及各车皮的位置，编程计算最优调度方案，使得移动车皮的总次数最少。

Input

第一行有2 个正整数n和k，表示车皮数为n和侧轨数为k。接下来的k+1行中，表示编号为0，1，2，…，k 的栈轨处按照从下到上的顺序停放的车皮序列。每行的第一个数表示该栈轨处的车皮数，紧接着是车皮序列。

Output

文件的第一行是最少移动次数m。接下来的m行是对应于最优方案的m次移动。每次移动用形如‘c x y’的3个整数来表示，其中c 表示车皮编号，x 表示起始栈轨号，y 表示目标栈轨号。如果无法调度则输出“No Solution!”。

Sample Input

6 2
4 4 1 5 3
2 6 2
0

Sample Output

9
3 0 1
5 0 2
1 0 3
3 1 2
2 1 3
3 2 3
4 0 3
5 2 3
6 1 3

题解

定义

\(top[]\)记录每一个栈的元素个数，\(mp[][]\)记录每一个栈的各个元素，\(Ansn\)和\(Ans[]\)记录答案个数已及答案，\(Res[]\)记录过程。

const int N=120,INF=999999;
int n,k,top[N],mp[N][N],Ansn;
struct node
{
	int c,x,y;
}Ans[N*N],Res[N*N];

读入

void Read()
{
	scanf("%d%d",&n,&k);
	for(int i=0;i<=k;++i)
	{
		scanf("%d",&top[i]);
		for(int j=1;j<=top[i];++j) scanf("%d",&mp[i][j]);
	}
	top[k+1]=0;
	for(int i=1;i<=n;++i) mp[k+1][i]=i;
}

回溯

回溯用了两个数组来记录上一步的状态。

void Copy(int (*tmpmp)[N],int mp[N][N],int *tmptop,int top[N])
{
	for(int i=0;i<=k+1;++i)
		for(int j=0;j<=n;++j) tmpmp[i][j]=mp[i][j];
	for(int i=0;i<=k+1;++i) tmptop[i]=top[i];
}

移动

\(Move(x,y,t)\)表示将\(x\)栈的顶部元素移至\(y\)栈，并且是第\(t\)步的操作。

void Move(int x,int y,int t)
{
	Res[t]=(node){mp[x][top[x]],x,y},
	mp[y][top[y]+1]=mp[x][top[x]],
	--top[x],++top[y];
}

进入第\(k+1\)个栈

\(Check\)函数返回值为\(1\)时，表示所有的都移动完成，即所有的数都进入了第\(k+1\)个栈。

bool Check(int &t)
{
	bool flag=1;
	while(flag)
	{
		flag=0;
		if(top[k+1]>=n)
		{
			if(t<Ansn)
			{
				Ansn=t;
				for(int i=1;i<=Ansn;++i) Ans[i]=Res[i];
			}
			return 1;
		}
		for(int i=0;i<=k;++i)
			if(top[i]&&mp[i][top[i]]==mp[k+1][top[k+1]+1])
			{
				Move(i,k+1,++t); flag=1;
			}
	}
	return 0;
}

\(DFS\)

这个只能靠自己去领悟……

void Dfs(int t)
{
	if(t>=Ansn) return;
	if(Check(t)) return;
	++t;
	int tmpmp[N][N],tmptop[N];
	Copy(tmpmp,mp,tmptop,top);
	for(int i=0;i<k;++i)
		for(int j=i+1;j<=k;++j)
			if(top[i]&&((!top[j])||(mp[i][top[i]]<mp[j][top[j]])))
			{
				Move(i,j,t);
				Dfs(t),
				Copy(mp,tmpmp,top,tmptop);
			}
}

输出

void Print()
{
	if(Ansn==INF)
	{
		puts("No Solution!");
		return;
	}
	printf("%d\n",Ansn);
	for(int i=1;i<=Ansn;++i) printf("%d %d %d\n",Ans[i].c,Ans[i].x,Ans[i].y);
}

整体代码

#include<iostream>
#include<cstdio>
using namespace std;

const int N=120,INF=999999;
int n,k,top[N],mp[N][N],Ansn;
struct node
{
	int c,x,y;
}Ans[N*N],Res[N*N];

void Read()
{
	scanf("%d%d",&n,&k);
	for(int i=0;i<=k;++i)
	{
		scanf("%d",&top[i]);
		for(int j=1;j<=top[i];++j) scanf("%d",&mp[i][j]);
	}
	top[k+1]=0;
	for(int i=1;i<=n;++i) mp[k+1][i]=i;
}

void Move(int x,int y,int t)
{
	Res[t]=(node){mp[x][top[x]],x,y},
	mp[y][top[y]+1]=mp[x][top[x]],
	--top[x],++top[y];
}

bool Check(int &t)
{
	bool flag=1;
	while(flag)
	{
		flag=0;
		if(top[k+1]>=n)
		{
			if(t<Ansn)
			{
				Ansn=t;
				for(int i=1;i<=Ansn;++i) Ans[i]=Res[i];
			}
			return 1;
		}
		for(int i=0;i<=k;++i)
			if(top[i]&&mp[i][top[i]]==mp[k+1][top[k+1]+1])
			{
				Move(i,k+1,++t); flag=1;
			}
	}
	return 0;
}

void Copy(int (*tmpmp)[N],int mp[N][N],int *tmptop,int top[N])
{
	for(int i=0;i<=k+1;++i)
		for(int j=0;j<=n;++j) tmpmp[i][j]=mp[i][j];
	for(int i=0;i<=k+1;++i) tmptop[i]=top[i];
}

void Dfs(int t)
{
	if(t>=Ansn) return;
	if(Check(t)) return;
	++t;
	int tmpmp[N][N],tmptop[N];
	Copy(tmpmp,mp,tmptop,top);
	for(int i=0;i<k;++i)
		for(int j=i+1;j<=k;++j)
			if(top[i]&&((!top[j])||(mp[i][top[i]]<mp[j][top[j]])))
			{
				Move(i,j,t);
				Dfs(t),
				Copy(mp,tmpmp,top,tmptop);
			}
}

void Print()
{
	if(Ansn==INF)
	{
		puts("No Solution!");
		return;
	}
	printf("%d\n",Ansn);
	for(int i=1;i<=Ansn;++i) printf("%d %d %d\n",Ans[i].c,Ans[i].x,Ans[i].y);
}

int main()
{
	Read(); Ansn=INF;
	Dfs(0),Print();
	return 0;
}