[POJ1101] The Game

Description

One morning, you wake up and think: "I am such a good programmer. Why not make some money?'' So you decide to write a computer game.
The game takes place on a rectangular board consisting of w * h squares. Each square might or might not contain a game piece, as shown in the picture.

One important aspect of the game is whether two game pieces can be connected by a path which satisfies the two following properties:

It consists of straight segments, each one being either horizontal or vertical.

It does not cross any other game pieces.

(It is allowed that the path leaves the board temporarily.)

Here is an example:

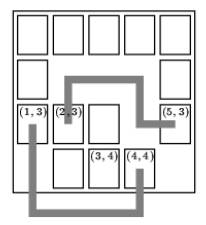
The game pieces at (1,3) and at (4, 4) can be connected. The game pieces at (2, 3) and (3, 4) cannot be connected; each path would cross at least one other game piece.

The part of the game you have to write now is the one testing whether two game pieces can be connected according to the rules above.

Input

The input contains descriptions of several different game situations. The first line of each description contains two integers w and h (1 <= w,h <= 75), the width and the height of the board. The next h lines describe the contents of the board; each of these lines contains exactly w characters: a "X" if there is a game piece at this location, and a space if there is no game piece.

Each description is followed by several lines containing four integers x1, y1, x2, y2 each satisfying 1 <= x1,x2 <= w, 1 <= y1,y2 <= h. These are the coordinates of two game pieces. (The upper left corner has the coordinates (1, 1).) These two game pieces will always be different. The list of pairs of game pieces for a board will be terminated by a line containing "0 0 0 0".

The entire input is terminated by a test case starting with w=h=0. This test case should not be procesed.

Output

For each board, output the line "Board #n:", where n is the number of the board. Then, output one line for each pair of game pieces associated with the board description. Each of these lines has to start with "Pair m: ", where m is the number of the pair (starting the count with 1 for each board). Follow this by "ksegments.", where k is the minimum number of segments for a path connecting the two game pieces, or "impossible.", if it is not possible to connect the two game pieces as described above.

Output a blank line after each board.

Sample Input

5 4
XXXXX
X   X
XXX X
 XXX 
2 3 5 3
1 3 4 4
2 3 3 4
0 0 0 0
0 0

Sample Output

Board #1:
Pair 1: 4 segments.
Pair 2: 3 segments.
Pair 3: impossible.

Source

Mid-Central European Regional Contest 1999

题意

一天清晨，你起床后想到：“我是一个这么牛的程序员，为什么不赚点钱呢？”所以，你决定写一个电脑游戏。 这个游戏是在一个长方形板上的，这个板由w*h个小正方形组成。每一个小正方形可能会包括一个游戏的块，如下图所示。

这个游戏的一个最重要的方面是判断两个块会不会由符合下列要求的路径连接。

1. 路径是由直的部分组成，每个部分或水平或垂直。

2. 路径不能跨过其它的游戏方块。（路径可以暂时离开板）

下面 举个例子。

（1,3）和（2,4）可以被连接。（2,3）和（3,4）不能被连接。 游戏的一部分 是你必须写一个程序证明两个木块是否能够被连接起来。

输入是多种情况的，第一行包括两个整数w和h(q<=w,h<=75)，即板的宽度和长度，下h行表示板上都有什么。每行包括w个字符，’X’表示有一个游戏方块，空格表示没有游戏方块。

每种情况后包括几行询问，每行包括4个整数X1,Y1,X2,Y2(1<=X1,X2<=w;I<=Y1,Y2<=h)。这是2个游戏片段的坐标。（左上角为坐标（1，1）。） 这两个坐标将永远是不同的。“0 0 0 0”表示输入结束。

整个输入结束 是输入了（0,0） 这个case不用考虑。

每个板，输出一行“Board #n:”，n是第n块板。然后输出一行为每对坐标是否相关联。如果关联，输出“Pair m: k segments.”m为这块板的第m次询问，k为路径包括几个部分。否则输出“Pair m: impossible.”

每个板询问完后输出个空行。

以上译文引自POJ 1101 简单BFS+题意

题解

\(BFS\)即可，加一个优化，除了对出发点要四个方向搜索直线外，对于其他点只要两个方向搜索，即当前点为上下，那么我们就搜左右；若当前点为左右，那么我们就搜上下。

但是这题恶心的地方在于：它的行列是反的，无语……。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
using namespace std;

const int maxnm=100;
int n,m,x1,y1,x2,y2,Ans;
char mp[maxnm][maxnm];
char Kg[maxnm];
int vis[maxnm][maxnm];
struct node
{
	int x,y,fq;
};
int fq[4][2]={{1,0},{0,1},{-1,0},{0,-1}};
queue<node> Q;

bool Check(int xx,int yy)
{
	if(xx<0||xx>n+1||yy<0||yy>m+1) return 0;
	return mp[xx][yy]!='X';
}

void Bfs()
{
	memset(vis,-1,sizeof(vis));
	vis[x1][y1]=0;
	while(!Q.empty()) Q.pop();
	int xx,yy;
	for(int i=0;i<4;++i)
	{
		xx=x1+fq[i][0],yy=y1+fq[i][1];
		while(Check(xx,yy))
		{
			if(vis[xx][yy]!=-1)
			{
				xx+=fq[i][0],yy+=fq[i][1];
				continue;
			}
			vis[xx][yy]=vis[x1][y1]+1;
			Q.push((node){xx,yy,i});
			xx+=fq[i][0],yy+=fq[i][1];
		}
		if(xx==x2&&yy==y2) {Ans=vis[x1][y1]+1;return;}
	}
	node top;
	while(!Q.empty())
	{
		top=Q.front(); Q.pop();
		for(int i=0;i<4;++i)
		{
			if(top.fq%2==i%2) continue;
			xx=top.x+fq[i][0],yy=top.y+fq[i][1];
			while(Check(xx,yy))
			{
				if(vis[xx][yy]!=-1)
				{
					xx+=fq[i][0],yy+=fq[i][1];
					continue;
				}
				vis[xx][yy]=vis[top.x][top.y]+1;
				Q.push((node){xx,yy,i});
				xx+=fq[i][0],yy+=fq[i][1];
			}
			if(xx==x2&&yy==y2) {Ans=vis[top.x][top.y]+1;return;}
		}
	}
}

int main()
{
	int T=0;
	for(scanf("%d%d",&m,&n);(n|m);scanf("%d%d",&m,&n))
	{
		printf("Board #%d:\n",++T);
		memset(mp,' ',sizeof(mp));
		gets(Kg);
		for(int i=1;i<=n;++i) gets(mp[i]+1);
		for(int i=1;;++i)
		{
			scanf("%d%d%d%d",&y1,&x1,&y2,&x2);
			if(!(x1|y1|x2|y2)) break;
			Ans=-1; Bfs();
			if(Ans==-1) printf("Pair %d: impossible.\n",i);
			else printf("Pair %d: %d segments.\n",i,Ans);
		}
		putchar('\n');//注意此处有换行
	}
	return 0;
}