园龄：4个月粉丝：3 关注：29 随笔 - 19 文章 - 6 评论 - 2 阅读 - 407

2024-10-30 12:55阅读: 13评论: 0推荐: 0

网络流的认识

# 网络流的认识 ## 什么是流网络网络（`network`）是指一个特殊的有向图

G = (V, E)

，其与一般有向图的不同之处在于有**容量和源汇点**，不考虑反向边。其中，我们有以下变量来方便表示： -

S

：源点 -

T

：汇点 -

c (u, v)

：表示从

u

到

v

这条有向边的**容量**为

c (u, v)

. -

f (u, v)

：表示从

u

到

v

这条有向边的**流量**为

f (u, v)

网络流的认识

什么是流网络

网络（network）是指一个特殊的有向图 $G = (V, E)$ ，其与一般有向图的不同之处在于有容量和源汇点，不考虑反向边。
其中，我们有以下变量来方便表示：

$S$ ：源点
$T$ ：汇点
$c (u, v)$ ：表示从 $u$ 到 $v$ 这条有向边的容量为 $c (u, v)$ .
$f (u, v)$ ：表示从 $u$ 到 $v$ 这条有向边的流量为 $f (u, v)$ .

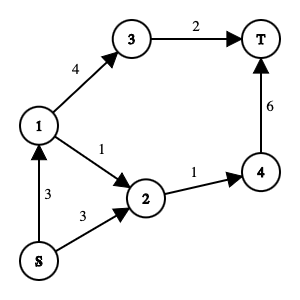
没有网络连接到洛谷图床

图 1

如上图，这就是一个流网络，其中 $c (1, 3) = 4$ 表示的就是 $1$ 到 $3$ 的容量为 $4$ ，源点 $S$ 往汇点 $T$ 进行流水操作，其中 $S$ 和 $T$ 能容下水的量是无限量的。（这里的水只是打个比方，因为很像自来水工厂为我们供水）。

什么是可行流

可行流，通俗点讲，就是在每条变分配流水的多少，使能满足条件（这个在生活实际也能推出）。
条件显然为以下：

流量限制： $0 \leq f (u, v) \leq c (u, v)$ ，你这条水管的流量如果大于容量，后果不堪设想。
流量守恒：抽象点讲，也就是你当前的点为 $u$ ，入点为 $p_{1}, p_{2}, \dots, p_{k 1}$ ，出点分别为 $q_{1}, q_{2}, \dots, q_{k 2}$ ，那么显然：

\sum_{i = 1}^{i \leq k 1} f (p_{i}, u) = \sum_{i = 1}^{i \leq k 2} f (u, q_{i})

形象点讲，也就是我当前流入到这个点的水的量最终都会流出到我可以到的点。

我们用 $f$ 表示一个可行流，如下图：

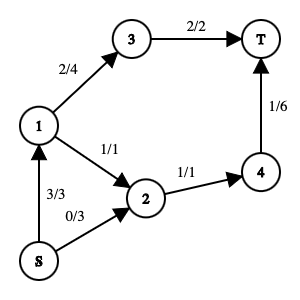
有网络连接到洛谷图床

图 2

其中在 $1$ 到 $3$ 这条边上， $f (1, 3) = 2$ ， $c (1, 3) = 4$ ，显然满足条件： $0 \leq f (1, 3) = 2 \leq 4 = c (1, 3)$ .
你可以试试看，能否满足第二个条件？

什么是最大流

最大流（也称最大可行流）实际是在可行流中找一个方案，使得流入汇点 $T$ 的水的量最大。我们用 $| f |$ 表示 $S$ 到 $T$ 点流量总和。根据定义显然有下种公式：

| f | = \sum_{(u, v) \in E} f (u, v) - \sum_{(u, v) \in E} f (v, u) .

在这里，右边的式子的第二个单项式 $\sum_{(u, v) \in E} f (v, u)$ 可以忽略不计，为了严谨，考虑了反向边的情况。

What is 残留网络

概念和构建

残留网络总是针对原图 $G = (V, E)$ 中的某一个可行流而言，因此，可以将残留网络看成是可行流的一个函数，通常记为 $G_{f}$ .
$G_{f} = (V_{f}, E_{f})$ ，其中 $V_{f} = V$ ， $E_{f} = E$ 和 $E$ 中所有的反向边。
残留网络中的容量记为 $c^{'} (u, v)$ ，且 $(u, v) \in E, (v, u) \in E$ ，定义为：

c^{'} (u, v) = {\begin{matrix} c (u, v) - f (u, v) (u, v) \in E \\ f (v, u) (u, v) \in E \end{matrix}

作用

可以通过 增广路径 的配合找到更大的流，使最后图中的最大流最大。

增广路径

定义

如果从源点 $S$ 出发沿着残留网络中容量大于 $0$ 的边走，可以走到汇点 $T$ ，那么将走过的边所组成的路径称为增广路径。
在这里我们发现：原网络可行流+残留网络可行流也是原网络的一个可行流
抽象点说（正式点说）， $f + f^{'}$ 属于 $G$ 的一个可行流，且有：

| f + f^{'} | = | f | + | f^{'} |

割

在网络中定点的一个划分，把所有顶点分成两个集合 $S$ 和 $T$ ，其中 $S \in S, T \in T$ ，而且有 $S \cup T = V, S \cap T = \emptyset$ ，记为 $[S, T]$ .

割的容量

指连接两个点集的边的容量总和，即 $c (S, T) = \sum_{u \in S} \sum_{v \in T} c (u, v)$

割的流量

指指连接两个点集的边的流量总和，
由上同理可得：

f (S, T) = \sum_{u \in S} \sum_{v \in T} (c (u, v) - c (v, u))

有反向边时， $c (v, u)$ 才有确值。
显然：

0 \leq f (S, T) \leq c (S, T)

最小割

指 $G$ 中所有割组成的集合中，容量最小的元素。

最大流最小割定理

以下 $3$ 个，知 $1$ 得 $2$ ：

$1$ 、 $f$ 是最大流
$2$ 、 $G_{f}$ 不存在增广路
$3$ 、 $\exists [S, T]$ ，满足 $| f | = c (S, T)$ （ $\exists$ 表示存在一个）。

证明：

证明 $1 \to 2$ ：
反证即可，若存在增广路就会使得当前的 $f$ 不是最大流，也就是 $| f | + | f^{'} | > | f |$ ，由条件又可知道： $| f |$ 最大，所以说当 $G_{f}$ 不存在增广路时， $f$ 为最大流。
证明 $2 \to 3$ ：
我们将对于 $G_{f}$ 中从 $S$ 出发沿着容量大于 $0$ 的边可以到达的点全部放入集合 $S$ 中，然后令 $T = V - S$ ，那么对于点 $x \in S, y \in Y$ ，边 $(x, y)$ 必有 $f (x, y) = c (x, y)$ 。
证明 $3 \to 1$ ：
因为 $| f | \leq 最大流 \leq c (S, T)$ ，而由 $3$ 可知 $| f | = c (S, T)$ ，故上式取等，即 $f$ 是最大流。

求最大流

基于上述定理，我们可以不断寻找增广路，利用增广路更新残留网络，直到找不到增广路，即可求得最大流。

EK 算法

时间复杂度 $O (n m^{2})$

Code1

#include<iostream>
#include<cstring>
using namespace std;

const int INF=1e9;
const int N=1005, M=10010;
int n, m, S, T;
struct node{
	int to, c, next;
}e[M<<1];
int h[N], tot;

// 残量网络建图，初始时正向的容量是 c, 反向容量是 0 。
void add(int u, int v, int c){
	e[tot].to=v, e[tot].c=c, e[tot].next=h[u], h[u]=tot++;
	e[tot].to=u, e[tot].c=0, e[tot].next=h[v], h[v]=tot++;	
}

int lim[N], pre[N]; // lim[u] 表示 S 到点 u 路径容量的最小值， pre[u] 表示 u 的前驱边。
bool vis[N];
int q[N];

// bfs 找增广路。
bool bfs(){
	memset(vis, false, sizeof vis);
	int hh=0, tt=-1;
	q[++tt]=S, vis[S]=true, lim[S]=INF;
	
	while(tt>=hh){
		int hd=q[hh++];
		for(int i=h[hd]; ~i; i=e[i].next){
			int go=e[i].to;
			if(vis[go] || !e[i].c) continue;
			vis[go]=true, q[++tt]=go;
			lim[go]=min(lim[hd], e[i].c);
			pre[go]=i;
			if(go==T) return true;
		}
	}
	return false;
}

int EK(){
	int res=0;
	while(bfs()){
		res+=lim[T];
		for(int i=T; i!=S; i=e[pre[i]^1].to){
			e[pre[i]].c-=lim[T], e[pre[i]^1].c+=lim[T];
		}
	}
	return res;
}
int main(){
	memset(h, -1, sizeof h);
	cin>>n>>m>>S>>T;
	while(m--){
		int u, v, c; cin>>u>>v>>c;
		add(u, v, c);
	}	
	cout<<EK()<<endl;
	return 0;
}

Code2

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <queue>
#include <cstring>
#define N 1007
#define M 10007
#define int long long
using namespace std;
const int INF = 1e9 + 7;
struct node{
	int to,val,nxt;
}e[M << 1];
int n, m, S, T, tot;
int head[N],dis[N],pre[N];
bool vis[N];
queue<int> q;
void add(int a,int b,int c) {
	e[tot].to = b, e[tot].val = c, e[tot].nxt = head[a], head[a] = tot++;
	e[tot].to = a, e[tot].val = 0, e[tot].nxt = head[b], head[b] = tot++;
}
bool bfs() {
	while(!q.empty()) q.pop();
	memset(vis,false,sizeof vis);
	q.push(S), vis[S] = true, dis[S] = INF;
	while(!q.empty()) {
		int t = q.front();
		q.pop();
		for (int i = head[t];i != -1;i = e[i].nxt) {
			int v = e[i].to;
			if (!vis[v] && e[i].val) {
				vis[v] = true;
				dis[v] = min(dis[t],e[i].val);
				pre[v] = i;
				if (v == T) return true;
				q.push(v);
			}
		}
	}
	return false;
}
int EK(){
	int r = 0;
	while(bfs()) {
		r += dis[T];
		for (int i = T;i != S;i = e[pre[i] ^ 1].to)
			e[pre[i]].val -= dis[T], e[pre[i] ^ 1].val += dis[T];
	}
	return r;
}

signed main(){
	cin >>n >> m >> S>> T;
	memset(head, -1,sizeof head);
	for(;m--;) {
		int a,b,c;
		cin >> a >> b >> c;
		add(a,b,c);
	}
	cout << EK();
	return 0;
}

Dinic 算法

多路增广，时间复杂度 $O (n^{2} m)$

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define gc() (st==ed&&(ed=(st=buf)+fread(buf,1,100000,stdin),st==ed)?EOF:*st++)
char buf[100001],*st=buf,*ed=buf;
void read(int &a){
    a=0;char c=gc();
    while(c>'9'||c<'0')c=gc();
    while(c>='0'&&c<='9')a=a*10+c-48,c=gc();
}

const int INF=0x3f3f3f3f;
const int N=10010, M=1e5+5;

struct node{
    int to, c, next;
}e[M<<1];
int h[N], tot;

void add(int u, int v, int cap){
    e[tot].to=v, e[tot].c=cap, e[tot].next=h[u], h[u]=tot++;
    e[tot].to=u, e[tot].c=0, e[tot].next=h[v], h[v]=tot++;  
}

int n, m, S, T;

int d[N], q[N], cur[N];

bool bfs(){
    memset(d, -1, sizeof d);
    int tt=-1, hh=0;
    q[++tt]=S, d[S]=0, cur[S]=h[S];

    while(tt>=hh){
        int hd=q[hh++];
        for(int i=h[hd]; ~i; i=e[i].next){
            int go=e[i].to;
            if(d[go]==-1 && e[i].c){
                d[go]=d[hd]+1;
                cur[go]=h[go];
                if(go==T) return true;
                q[++tt]=go;
            }
        }
    }
    return false;
}

int find(int u, int limit){
    if(u==T) return limit;
    int flow=0;
    for(int i=cur[u]; ~i && flow<limit; i=e[i].next){
        cur[u]=i;
        int go=e[i].to;
        if(d[go]==d[u]+1 && e[i].c){
            int t=find(go, min(e[i].c, limit-flow));
            if(!t) d[go]=-1;
            e[i].c-=t, e[i^1].c+=t, flow+=t;
        }
    }
    return flow;
}

int dinic(){
    int res=0, flow;
    while(bfs()) while(flow=find(S, INF)) res+=flow;
    return res;
}

signed main(){
    memset(h, -1, sizeof h);
    read(n), read(m), read(S), read(T);
    while(m--){
        int u, v, cap; read(u), read(v), read(cap);
        add(u, v, cap);
    }

    cout<<dinic()<<endl;

    return 0;
}

完结。

上一篇P1779 魔鬼杀手题解&&思路

本文作者：high-sky

本文链接：https://www.cnblogs.com/high-sky/p/18515629

posted @ 2024-10-30 12:55 high_skyy 阅读(13) 评论(0) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

high-sky

网络流的认识

网络流的认识

什么是流网络

什么是可行流

什么是最大流

What is 残留网络

概念和构建

作用

增广路径

定义

割

割的容量

割的流量

最小割

最大流最小割定理

求最大流

EK 算法

Code1

Code2

Dinic 算法

公告

搜索

常用链接

我的标签

合集

随笔分类

随笔档案

文章分类

相册

阅读排行榜

评论排行榜

推荐排行榜

最新评论