算法-动态规划-01背包
0. 动态规划五部曲：
- 确定dp数组（dp table）以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组
1. 爬楼梯(LeetCode 70)
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？
思路：
- 确定递推公式，因为只依赖前两个状态，所以可以进行状态压缩，只设置3个变量
class Solution {
// 递推公式和斐波那契相同
// f(n) = f(n-1) + f(n-2)
public int climbStairs(int n) {
if(n < 3) return n;
int a = 1, b = 2, c = 0;
for(int i = 3; i<=n; ++i) {
c = a+b;
a = b;
b = c;
}
return c;
}
}
2. 使用最小花费爬楼梯(LeetCode 746)
给你一个整数数组 cost ，其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。
一旦你支付此费用，即可选择向上爬一个或者两个台阶。
你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。
请你计算并返回达到楼梯顶部的最低花费。
输入：cost = [10,15,20]
输出：15
解释：你将从下标为 1 的台阶开始。
- 支付 15 ，向上爬两个台阶，到达楼梯顶部。
总花费为 15 。
class Solution {
public int minCostClimbingStairs(int[] cost) {
int[] dp = new int[cost.length+1];
dp[0] = 0;
dp[1] = 0;
for(int i = 2; i<=cost.length; ++i) {
dp[i] = Math.min(dp[i-2]+cost[i-2], dp[i-1]+cost[i-1]);
}
return dp[cost.length];
}
}
3. 不同路径(LeetCode 62)
一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish”）。
问总共有多少条不同的路径？
class Solution {
public int uniquePaths(int m, int n) {
int[][] dp = new int[m][n];
for(int i = 0; i<m; ++i) {
dp[i][0] = 1;
}
for(int j = 0; j<n; ++j) {
dp[0][j] = 1;
}
for(int i = 1; i<m; ++i) {
for(int j = 1; j<n; ++j) {
dp[i][j] = dp[i-1][j] + dp[i][j-1];
}
}
return dp[m-1][n-1];
}
}
4. 不同路径 II(LeetCode 63)
一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish”）。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？
网格中的障碍物和空位置分别用 1 和 0 来表示。
注意：
- 本题利用了java的int数组默认初值是0来简化代码。
class Solution {
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
int m = obstacleGrid.length, n = obstacleGrid[0].length;
int[][] dp = new int[m][n];
for(int i = 0; i < n && obstacleGrid[0][i] == 0; ++i) {
dp[0][i] = 1;
}
for(int j = 0; j < m && obstacleGrid[j][0] == 0; ++j) {
dp[j][0] = 1;
}
for(int i = 1; i<m; ++i) {
for(int j = 1; j<n; ++j) {
dp[i][j] = (obstacleGrid[i][j] == 0) ? dp[i-1][j] + dp[i][j-1] : 0;
}
}
return dp[m-1][n-1];
}
}
5. 整数拆分(LeetCode 343)
给定一个正整数 n ，将其拆分为 k 个 正整数 的和（ k >= 2 ），并使这些整数的乘积最大化。
返回你可以获得的最大乘积。
输入: n = 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。
注意：
- 递推公式不太好想
- j的循环终止条件换成i/2也是成立的，但是没那么好理解
class Solution {
public int integerBreak(int n) {
int[] dp = new int[n+1];
dp[2] = 1;
for(int i = 3; i<=n; ++i) {
for(int j = 1; j<=i; ++j) {
// 拆成两份后相乘，还是继续拆分
// 如果大于原来的值，则更新
dp[i] = Math.max(dp[i], Math.max(j * (i-j), j * dp[i-j]));
}
}
return dp[n];
}
}
6. 不同的二叉搜索树
给你一个整数n，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的二叉搜索树有多少种？
返回满足题意的二叉搜索树的种数。
思路：
- 子树中节点的数值不重要，因为二叉搜索树的结构只和大小序列相关
- 第二层for循环表示在节点总数为i时，选择不同的节点作为根节点，进而左子树上的节点数量不同，树的结构不同
class Solution {
public int numTrees(int n) {
int[] dp = new int[n+1];
dp[0] = 1;
dp[1] = 1;
for(int i = 2; i<=n; ++i) {
// j表示左子树上的节点数，i-1-j表示右子树上的节点数
for(int j = 0; j<=i-1; ++j) {
// 左树的种类 * 右数的种类
dp[i] += dp[j] * dp[i-1-j];
}
}
return dp[n];
}
}
7. 0-1背包问题
7.1 二维dp数组
关键：理解dp[][]数组的含义
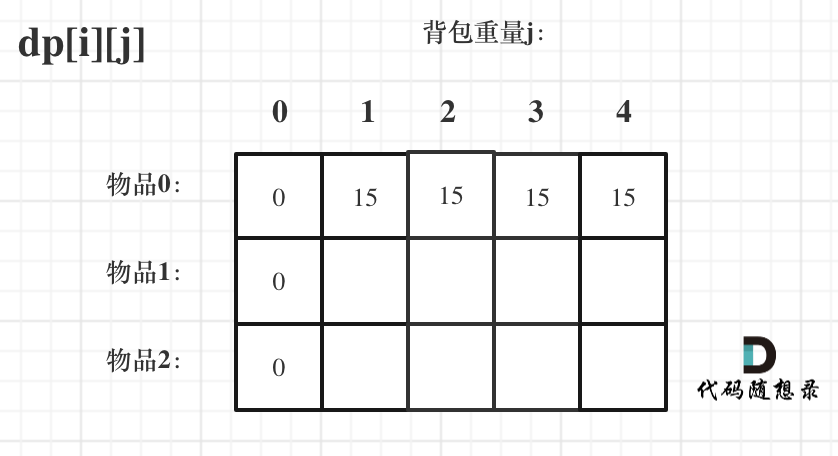
- 维度：
dp[n][totalWeight+1]，其中n表示可选物品的数量，totalWeight表示背包可容纳的最大重量 - 含义：
dp[i][j]表示编号为0到i的物品任选，背包容量为j，能获得的最大价值 - 初始化：初始化第一行，只考虑第一个物品，重量够了就选，不够就不能选
- 递推公式：
// j不小于weight[i]，才考虑是否要取物品i；否则直接继承dp[i-1][j]
if(j >= weight[i])
dp[i][j] = Math.max(dp[i-1][j], dp[i-1][j-weight[i]] + value[i])
else
dp[i][j] = dp[i-1][j];
import java.util.Scanner;
// 0-1背包问题
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
// 物品的数量
int n = scanner.nextInt();
// 背包的总容量
int totalWeight = scanner.nextInt();
int[] weight = new int[n];
int[] value = new int[n];
for(int i = 0; i<n; ++i) {
weight[i] = scanner.nextInt();
}
for(int i = 0; i<n; ++i) {
value[i] = scanner.nextInt();
}
int[][] dp = new int[n][totalWeight+1];
// 初始化第一行
for(int j = 0; j<=totalWeight; ++j) {
if(j >= weight[0])
dp[0][j] = value[0];
}
for(int i = 1; i<n; ++i) {
for(int j = 1; j<=totalWeight; ++j) {
if(j>=weight[i])
dp[i][j] = Math.max(dp[i-1][j], dp[i-1][j-weight[i]]+value[i]);
else
dp[i][j] = dp[i-1][j];
}
}
System.out.println(dp[n-1][totalWeight]);
}
}
7.2 一维dp数组
使用一维dp数组能够
- 节省从上一行复制到下一行的时间
- 减少空间开销
注意：
- 在遍历重量的for循环时，需要进行倒序遍历，防止第i个问题被重复选取。
import java.util.Scanner;
// 0-1背包问题
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
// 物品的数量
int n = scanner.nextInt();
// 背包的总容量
int totalWeight = scanner.nextInt();
int[] weight = new int[n];
int[] value = new int[n];
for(int i = 0; i<n; ++i) {
weight[i] = scanner.nextInt();
}
for(int i = 0; i<n; ++i) {
value[i] = scanner.nextInt();
}
int[] dp = new int[totalWeight+1];
// 初始化
for(int j = 0; j<=totalWeight; ++j) {
if(j >= weight[0])
dp[j] = value[0];
}
for(int i = 1; i<n; ++i) {
for(int j = totalWeight; j>=0; j--) {
if(j>=weight[i])
dp[j] = Math.max(dp[j], dp[j-weight[i]]+value[i]);
}
}
System.out.println(dp[totalWeight]);
}
}
8. 分割等和子集(LeetCode 416)
给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。
思路：
- 将问题转化为0-1背包，判断能否用nums[]中的元素填满容量为half的背包，即是否满足
dp[half] == half
class Solution {
public boolean canPartition(int[] nums) {
int sum = 0, half = 0;
for(int i = 0; i<nums.length; ++i) {
sum += nums[i];
}
if(sum % 2 == 1)
return false;
else
half = sum/2;
int[] dp = new int[half+1];
// 初始化dp数组
for(int j = nums[0]; j<=half; ++j) {
dp[j] = nums[0];
}
// 一维数组的内层循环需要反向遍历
for(int i = 1; i<nums.length; ++i) {
for(int j = half; j>=nums[i]; --j) {
dp[j] = Math.max(dp[j], dp[j-nums[i]] + nums[i]);
}
}
return (dp[half] == half);
}
}
9. 最后一块石头的重量II(LeetCode 1049)
有一堆石头，用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。
每一回合，从中选出任意两块石头，然后将它们一起粉碎。假设石头的重量分别为 x 和 y，且 x <= y。那么粉碎的可能结果如下：
如果 x == y，那么两块石头都会被完全粉碎；
如果 x != y，那么重量为 x 的石头将会完全粉碎，而重量为 y 的石头新重量为 y-x。
最后，最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下，就返回 0。
class Solution {
// 将石头划分为重量相近的两堆
public int lastStoneWeightII(int[] stones) {
int sum = 0, half = 0;
for(int i = 0; i<stones.length; ++i) {
sum += stones[i];
}
half = sum/2;
int[] dp = new int[half+1];
for(int i = 0; i<stones.length; ++i) {
for(int j = half; j>=stones[i]; --j) {
dp[j] = Math.max(dp[j], dp[j - stones[i]] + stones[i]);
}
}
// dp[half]中存的是小堆中的重量
return ((sum - dp[half]) - dp[half]);
}
}
10. 目标和(LeetCode 494)
给你一个非负整数数组 nums 和一个整数 target 。
向数组中的每个整数前添加 '+' 或 '-' ，然后串联起所有整数，可以构造一个 表达式 ：
例如，nums = [2, 1] ，可以在 2 之前添加 '+' ，在 1 之前添加 '-' ，然后串联起来得到表达式 "+2-1" 。
返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。
输入：nums = [1,1,1,1,1], target = 3
输出：5
解释：一共有 5 种方法让最终目标和为 3 。
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3
思路：
- 相同点：本质上仍然是将数组分为两份
- 不同点：此处统计的是将背包填满的方案数，递归方程因此变为
if(nums[i] > j) dp[i][j] = dp[i-1][j] + dp[i-1][j-nums[i]]
class Solution {
// 二维dp数组解法
public int findTargetSumWays(int[] nums, int target) {
int sum = 0;
for(int i = 0; i<nums.length; ++i) {
sum += nums[i];
}
if(Math.abs(target) > sum) return 0;
if((target + sum) % 2 == 1) return 0;
int positive = (target + sum)/2;
int n = nums.length;
// dp[i][j]表示背包容量为j时，只从前i个元素中选择能填满背包的方案数
int[][] dp = new int[n][positive+1];
// 初始化第一行
if(positive >= nums[0])
dp[0][nums[0]] = 1;
// 初始化第一列
int zeroCount = 0;
for(int i = 0; i<n; ++i) {
if(nums[i] == 0)
zeroCount++;
dp[i][0] = (int) Math.pow(2, zeroCount);
}
for(int i = 1; i<n; ++i) {
for(int j = 1; j<=positive; ++j) {
if(j<nums[i])
dp[i][j] = dp[i-1][j];
else
// 不选nums[i]的种类 + 选nums[i]的种类
dp[i][j] = dp[i-1][j] + dp[i-1][j-nums[i]];
}
}
return dp[n-1][positive];
}
}
11. 一和零(LeetCode 474)
给你一个二进制字符串数组 strs 和两个整数 m 和 n 。
请你找出并返回 strs 的最大子集的长度，该子集中最多有m个0和n个1。
思路：
- 本题仍然是
01背包，01背包指每个物品只有一个，只有选或不选两种选项。 - 因为有
0的数量和1的数量两个限制，本题是二维背包 - 正常应该采用三维dp数组，压缩后可以使用二维dp数组（需要进行倒序遍历）
class Solution {
public int findMaxForm(String[] strs, int m, int n) {
// dp[i][j]表示最多有i个0，j个1时的最大子集长度
int[][] dp = new int[m+1][n+1];
int oneCount = 0, zeroCount = 0;
for(String str : strs){
zeroCount = 0;
oneCount = 0;
for(int k = 0; k<str.length(); ++k) {
if(str.charAt(k) == '0')
zeroCount++;
else
oneCount++;
}
// 倒序遍历
for(int i = m; i >= zeroCount; --i) {
for(int j = n; j >= oneCount; --j) {
dp[i][j] = Math.max(dp[i][j], dp[i-zeroCount][j-oneCount] + 1);
}
}
}
return dp[m][n];
}
}
