pytoch的最佳打开方式
import numpy as np
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
%matplotlib inline
从张量（tensor）开始
张量是个抽象的概念， 它是数据的容器， 通过几个例子来理解吧。
- 0维张量/标量:标量是一个数字
- 1维张量/向量:1维张量称为“向量”
- 2维张量:2维张量称为矩阵
张量可以有任意的维度
定义张量
torch.ones(4, 2)
tensor([[1., 1.],
[1., 1.],
[1., 1.],
[1., 1.]])
torch.zeros(4, 2)
tensor([[0., 0.],
[0., 0.],
[0., 0.],
[0., 0.]])
torch.tensor([1, 3, 4, 5, 6])
tensor([1, 3, 4, 5, 6])
张量的存储
points = torch.tensor([[1.0, 4.0], [2.0, 1.0], [3.0, 5.0]])
# 按照存储顺序显示元素
points.storage()
1.0
4.0
2.0
1.0
3.0
5.0
[torch.FloatStorage of size 6]
#从存储地址更改元素
points_storage = points.storage()
points_storage[1] = 0.0 # 原来4的位置改成了0
points
tensor([[1., 0.],
[2., 1.],
[3., 5.]])
张量的操作
points.t() # 转置
tensor([[1., 2., 3.],
[0., 1., 5.]])
# 多维张量的转置
some_tensor = torch.ones(3, 4, 5)
some_tensor_t = some_tensor.transpose(0, 2)
some_tensor_t.shape # 交换3， 5
torch.Size([5, 4, 3])
与numpy交互
points = torch.ones(3, 4)
points_np = points.numpy() # torch转numpy
points_np
array([[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.]], dtype=float32)
torch.from_numpy(points_np) # numpy转torch
tensor([[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.]])
一个实例
data = torch.rand(10, 10) #生成10行10列的随机数据，当做10组拥有10个特征的数据
target = torch.randint(0, 3, (10,)) #生成随机值为0、1或2的10个数据，当做10个标签
target
tensor([0, 1, 0, 1, 1, 0, 0, 0, 2, 2])
# onehot一下（onehot就是将标签0/1化）
target_onehot = torch.zeros(target.shape[0], 3)
target_onehot.scatter_(1, target.unsqueeze(1), 1.0) # unsqueeze(1)在“1”方向上，增加一个维度
tensor([[1., 0., 0.],
[0., 1., 0.],
[1., 0., 0.],
[0., 1., 0.],
[0., 1., 0.],
[1., 0., 0.],
[1., 0., 0.],
[1., 0., 0.],
[0., 0., 1.],
[0., 0., 1.]])
# unsqueeze深入理解
torch.zeros(2, 2, 3).unsqueeze(3).shape #"在3方向上增加维度"
torch.Size([2, 2, 3, 1])
#正则化
data_mean = torch.mean(data, dim=0)
data_var = torch.var(data, dim=0)
data_normalized = (data - data_mean) / data_var
#数据选择
data[torch.le(target, 1)].shape # 选择标签小于等于1的数据
#le小于等于, ge大于等于, lt小于, gt大于
torch.Size([8, 10])
# 将第一列和第二列抽出
torch.stack((data[:, 0], data[:, 1]), 1).shape
torch.Size([10, 2])
动手实现一个模型
定义模型
- 模型 \(y = w*x + b\)
- 损失函数 \(f(y) = (y - \hat y )^2\)
定义数据
X = [3.57, 5.59, 5.82, 8.19, 5.63, 4.89, 3.39, 2.18, 4.84, 6.04, 6.84]
y = [0.5, 14.0, 15.0, 28.0, 11.0, 8.0, 3.0, -4.0, 6.0, 13.0, 21.0]
# 转换成张量
X = torch.tensor(X)
y = torch.tensor(y)
模型实现
#定义模型
def model(X, w, b):
return w*X + b
#定义损失函数
def Loss(y, y_pred):
return ((y - y_pred)**2).mean()
#初始化参数
w = torch.ones(1)
b = torch.zeros(1)
Loss(y, model(X, w, b)) # 损失值
tensor(80.3643)
#参数w下降的梯度
delta = 1e-2
loss_rate_of_change_w = \
(Loss(model(X, w + delta, b), y) -
Loss(model(X, w - delta, b), y)) / (2.0 * delta)
#参数b下降的梯度
loss_rate_of_change_b = \
(Loss(model(X, w, b + delta), y) -
Loss(model(X, w, b - delta), y)) / (2.0 * delta)
这样求w，b的梯度有很大缺点
- 拓展性不强，新的参数需要重新定义
- delta的值不好选择
于是我们想到用链式求导法则
\[\frac{d_{L}}{d_w} = \frac{d_{L}}{d_p} * \frac{d_p}{d_w} \\
\frac{d_{L}}{d_b} = \frac{d_{L}}{d_p} * \frac{d_p}{d_b}\]
#对y求导
def dLoss(y, y_pred):
return 2*(y_pred - y)
#对w求导
def dw(X, w, b):
return X
#对b求导
def db(X, w, b):
return 1.0
#整个的梯度下降函数
def Grad(X, y, y_pred, w, b):
d_w = dLoss(y, y_pred) * dw(X, w, b)
d_b = dLoss(y, y_pred) * db(X, w, b)
return torch.stack([d_w.mean(), d_b.mean()])
#训练过程
def train(n_epochs, lr, params, X, y):
'''
n_epochs:循环次数
lr:学习率
params:模型参数
'''
for epoch in range(n_epochs):
w, b = params
y_pred = model(X, w, b) #预测值
loss = Loss(y, y_pred) #损失值
grad = Grad(X, y, y_pred, w, b) #梯度
params -= lr*grad #参数更新
if(epoch%500 == 0):
print('Epoch %d, Loss %f' % (epoch, float(loss)))#500轮打印一次
return params
#测试一下
params = train(
n_epochs=3000,
lr = 1e-2,
params = torch.tensor([1.0, 0.0]),
X = X,
y = y)
params
Epoch 0, Loss 80.364349
Epoch 500, Loss 7.843370
Epoch 1000, Loss 3.825482
Epoch 1500, Loss 3.091631
Epoch 2000, Loss 2.957596
Epoch 2500, Loss 2.933116
tensor([ 5.3489, -17.1980])
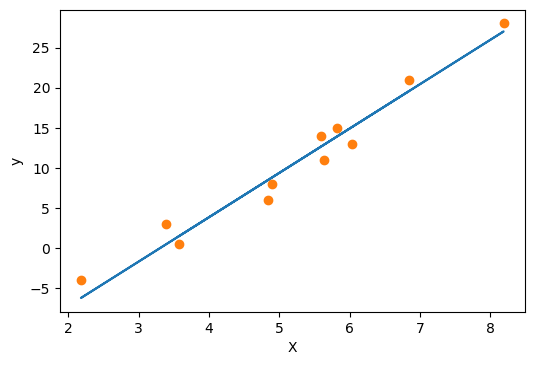
# 可视化
fig = plt.figure(dpi=100)
plt.xlabel("X")
plt.ylabel("y")
y_pred = model(X, *params)
plt.plot(X.numpy(), y_pred.numpy())
plt.plot(X.numpy(), y.numpy(), 'o')
plt.show()
以上，我们动手实现了一个线性模型，但是还有很多地方可以优化的，比如，更改模型为$y = w_1 * x^2 + w_0 * x +b $则该模型不适用，而且没有验证集，此外， 求梯度可以交给pytorch中的autograd，下面我们一个个的来优化
使用pytoch优化你的模型
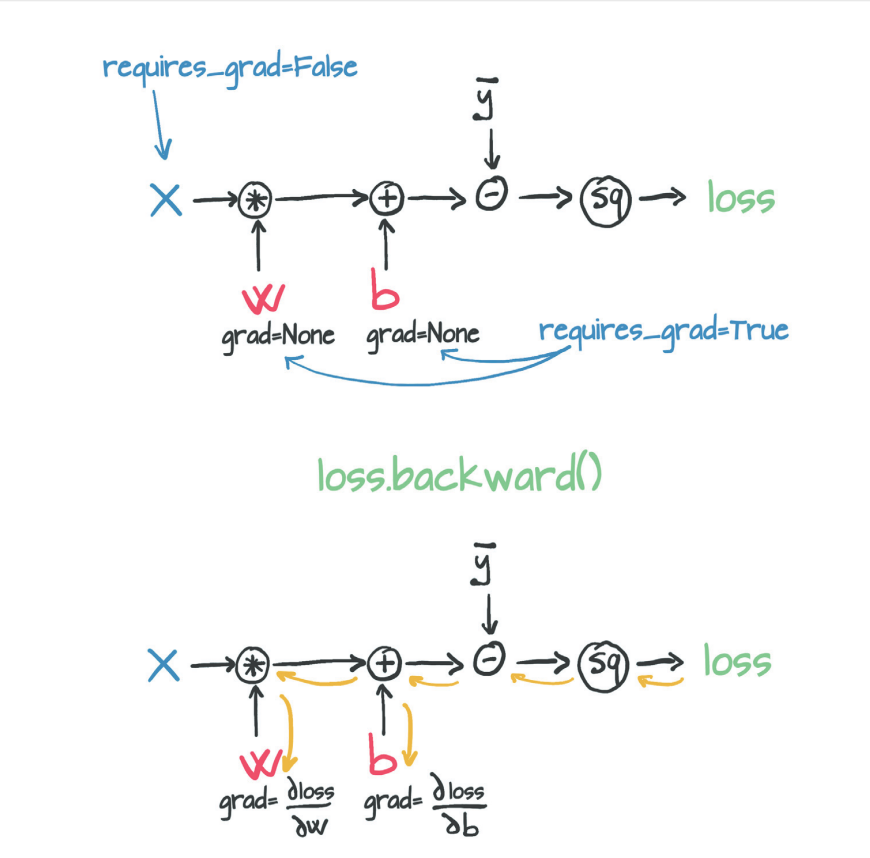
使用pytorch中的autograd
#requires_grad=True,pytorch会跟踪由参数操作产生的张量的整个家谱。
params = torch.tensor([1.0, 0.0], requires_grad=True)
params.grad is None
True
loss = Loss(model(X, *params), y)
loss.backward()
params.grad # params的grad属性包含损失对params的每个元素的导数
tensor([-77.6140, -10.6400])
Attention:调用后向会导致导数在叶节点处累积。在使用渐变进行参数更新之后，需要显式地将其归零。
#一定要归零
if params.grad is not None:
params.grad.zero_()
params.grad
tensor([0., 0.])
# 将autograd添加到模型中
def train(n_epochs, lr, params, X, y):
for epoch in range(n_epochs):
if params.grad is not None:
paras.grad.zero_()
y_pred = model(X, *params)
loss = Loss(y, y_pred)
loss.backward()
params = (params - lr*params.grad).detach().requires_grad_()
if(epoch%500 == 0):
print('Epoch %d, Loss %f' % (epoch, float(loss)))#500轮打印一次
return params
解释一下.detach() 和 .requires_grad_()
-
通过调用.detatch()将新的params张量从与其更新表达式相关的计算图中分离出来。这样，params就有效地丢失了生成它的操作的内存。
-
通过调用.requires_grad_()重新启用跟踪。
#测试一下,params开启autograd
params = train(
n_epochs=3000,
lr = 1e-2,
params = torch.tensor([1.0, 0.0], requires_grad = True),
X = X,
y = y)
params
Epoch 0, Loss 80.364349
Epoch 500, Loss 7.843370
Epoch 1000, Loss 3.825482
Epoch 1500, Loss 3.091631
Epoch 2000, Loss 2.957596
Epoch 2500, Loss 2.933116
tensor([ 5.3489, -17.1980], requires_grad=True)
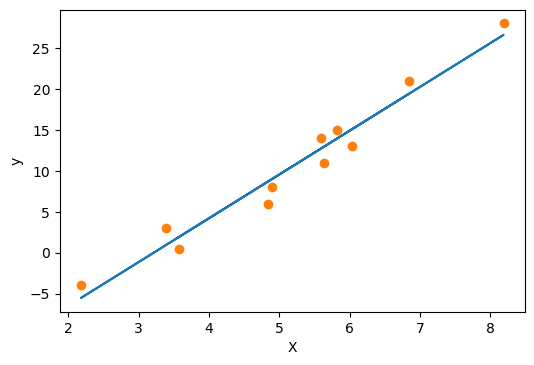
# 可视化一下
fig = plt.figure(dpi=100)
plt.xlabel("X")
plt.ylabel("y")
y_pred = model(X, *params)
plt.plot(X.numpy(), y_pred.detach().numpy())
plt.plot(X.numpy(), y.numpy(), 'o')
plt.show()
将model改成$y = w_1 * x^2 + w_0 * x +b$，上面的模型应该如何修改？
## 使用pytorch中的优化器optim
import torch.optim as optim
dir(optim)
['ASGD',
'Adadelta',
'Adagrad',
'Adam',
'AdamW',
'Adamax',
'LBFGS',
'Optimizer',
'RMSprop',
'Rprop',
'SGD',
'SparseAdam',
'__builtins__',
'__cached__',
'__doc__',
'__file__',
'__loader__',
'__name__',
'__package__',
'__path__',
'__spec__',
'lr_scheduler']
# 定义一个优化器
params = torch.tensor([1.0, 0.0], requires_grad = True)
lr = 1e-2
optimizer = optim.SGD([params], lr = lr) #换成Adam试试
# 将optimizer添加到模型中
def train(n_epochs, optimizer, params, X, y):
for epoch in range(n_epochs):
y_pred = model(X, *params)
loss = Loss(y, y_pred)
optimizer.zero_grad()
loss.backward()
optimizer.step() # 通过step方法完成params的更新
if(epoch%500 == 0):
print('Epoch %d, Loss %f' % (epoch, float(loss)))#500轮打印一次
return params
#测试一下, 将lr改成optimizer
params = train(
n_epochs = 3000,
optimizer = optimizer,
params = params,
X = X,
y = y)
params
Epoch 0, Loss 80.364349
Epoch 500, Loss 7.843370
Epoch 1000, Loss 3.825482
Epoch 1500, Loss 3.091631
Epoch 2000, Loss 2.957596
Epoch 2500, Loss 2.933116
tensor([ 5.3489, -17.1980], requires_grad=True)
# 可视化一下
fig = plt.figure(dpi=100)
plt.xlabel("X")
plt.ylabel("y")
y_pred = model(X, *params)
plt.plot(X.numpy(), y_pred.detach().numpy())
plt.plot(X.numpy(), y.numpy(), 'o')
plt.show()
加入验证集
#将数据划分成训练集和验证集
n_samples = X.shape[0]
n_val = int(0.2*n_samples) #20%的数据做验证集
shuffled_indices = torch.randperm(n_samples) #打乱顺序
train_indices = shuffled_indices[n_val:-1]
val_indices = shuffled_indices[:n_val]
X_train = X[train_indices]
X_val = X[val_indices]
y_train = y[train_indices]
y_val = y[val_indices]
print("数据集", X)
print("训练集", X_train)
print("验证集", X_val)
数据集 tensor([3.5700, 5.5900, 5.8200, 8.1900, 5.6300, 4.8900, 3.3900, 2.1800, 4.8400,
6.0400, 6.8400])
训练集 tensor([3.3900, 5.8200, 4.8900, 3.5700, 6.8400, 6.0400, 4.8400, 5.5900])
验证集 tensor([8.1900, 2.1800])
# 将验证集添加到模型中
def train(n_epochs, optimizer, params, X_train, y_train, X_val, y_val):
for epoch in range(n_epochs):
y_train_pred = model(X_train, *params)
loss_train = Loss(y_train, y_train_pred)
y_val_pred = model(X_val, *params)
loss_val = Loss(y_val, y_val_pred)
optimizer.zero_grad()
loss_train.backward()
optimizer.step() # 通过step方法完成params的更新
if(epoch%500 == 0):
print('Epoch %d, Training Loss %f Validation Loss %d' \
% (epoch, float(loss_train), float(loss_val)))#500轮打印一次
return params
#测试一下, 将lr改成optimizer
params = train(
n_epochs = 5000,
optimizer = optimizer,
params = params,
X_train = X_train,
y_train = y_train,
X_val = X_val,
y_val = y_val)
params
Epoch 0, Training Loss 2.973095 Validation Loss 2
Epoch 500, Training Loss 2.972950 Validation Loss 2
Epoch 1000, Training Loss 2.972893 Validation Loss 2
Epoch 1500, Training Loss 2.972868 Validation Loss 2
Epoch 2000, Training Loss 2.972858 Validation Loss 2
Epoch 2500, Training Loss 2.972854 Validation Loss 2
Epoch 3000, Training Loss 2.972851 Validation Loss 2
Epoch 3500, Training Loss 2.972849 Validation Loss 2
Epoch 4000, Training Loss 2.972851 Validation Loss 2
Epoch 4500, Training Loss 2.972849 Validation Loss 2
tensor([ 5.5238, -18.2330], requires_grad=True)
# 可视化一下
fig = plt.figure(dpi=100)
plt.xlabel("X")
plt.ylabel("y")
y_pred = model(X, *params)
plt.plot(X.numpy(), y_pred.detach().numpy())
plt.plot(X.numpy(), y.numpy(), 'o')
plt.show()
使用pytorch中的模型
import torch.nn as nn
Linear_model = nn.Linear(1, 1) # 两个参数分别是输入输出大小
# 模型的一些方法
print(Linear_model.weight)
print(Linear_model.bias)
Parameter containing:
tensor([[0.5101]], requires_grad=True)
Parameter containing:
tensor([0.0583], requires_grad=True)
# 测试下线性模型
xx = torch.arange(0, 10, 0.1).unsqueeze(1) #这里一定是二维哦
yy = Linear_model(xx)
fig = plt.figure(dpi=100)
plt.xlabel("xx")
plt.ylabel("yy")
plt.plot(xx.numpy(), yy.detach().numpy())
plt.show()
神经网络中的任何模块都被编写成同时产生一批多个输入的输出。因此，假设您需要对B个样本运行nn.Linear，你可以创建一个大小为B x Nin的输入张量，其中B是批量的大小，Nin是输入特征的数量。所以X, y的维度需要作出一些调整。
X.shape # 需要改成 11 × 1的形状
torch.Size([11])
#改变数据的维度
X = X.unsqueeze(1)
y = y.unsqueeze(1)
#将数据划分成训练集和验证集
n_samples = X.shape[0]
n_val = int(0.2*n_samples) #20%的数据做验证集
shuffled_indices = torch.randperm(n_samples) #打乱顺序
train_indices = shuffled_indices[n_val:-1]
val_indices = shuffled_indices[:n_val]
X_train = X[train_indices]
X_val = X[val_indices]
y_train = y[train_indices]
y_val = y[val_indices]
# 将Linear_model添加到模型中，还直接使用了nn中的MSELoss计算损失
# 另外，函数不需要返回值， 参数都在Linear_model中
def train(n_epochs, optimizer, model, Loss, X_train, y_train,
X_val, y_val):
for epoch in range(n_epochs):
y_train_pred = model(X_train)
loss_train = Loss(y_train, y_train_pred)
y_val_pred = model(X_val)
loss_val = Loss(y_val, y_val_pred)
optimizer.zero_grad()
loss_train.backward()
optimizer.step() # 通过step方法完成params的更新
if(epoch%500 == 0):
print('Epoch %d, Training Loss %f Validation Loss %d' \
% (epoch, float(loss_train), float(loss_val)))#500轮打印一次
#optimizer需要改一下， params直接使用Linear_model中的parameters方法
optimizer = optim.SGD(Linear_model.parameters(), lr=1e-2)
#测试一下, 注意参数， 另外添加了nn中的MSELoss计算损失
train(
n_epochs = 5000,
optimizer = optimizer,
model = Linear_model,
Loss = nn.MSELoss(),
X_train = X_train,
y_train = y_train,
X_val = X_val,
y_val = y_val)
Epoch 0, Training Loss 88.300812 Validation Loss 283
Epoch 500, Training Loss 8.619841 Validation Loss 20
Epoch 1000, Training Loss 4.161697 Validation Loss 7
Epoch 1500, Training Loss 3.029744 Validation Loss 4
Epoch 2000, Training Loss 2.742332 Validation Loss 3
Epoch 2500, Training Loss 2.669355 Validation Loss 3
Epoch 3000, Training Loss 2.650826 Validation Loss 3
Epoch 3500, Training Loss 2.646122 Validation Loss 3
Epoch 4000, Training Loss 2.644927 Validation Loss 3
Epoch 4500, Training Loss 2.644624 Validation Loss 3
# 可视化一下
fig = plt.figure(dpi=100)
plt.xlabel("X")
plt.ylabel("y")
y_pred = Linear_model(X)
plt.plot(X.numpy(), y_pred.detach().numpy())
plt.plot(X.numpy(), y.numpy(), 'o')
plt.show()
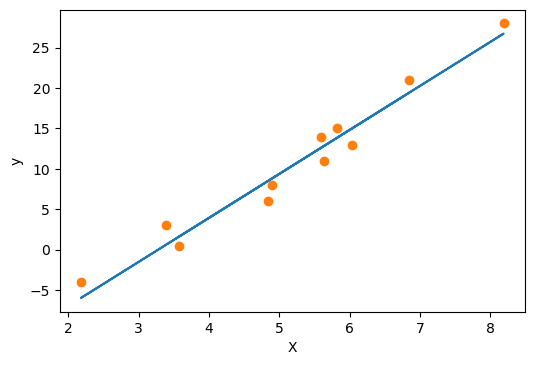
使用神经网络
#nn提供了一种通过神经网络连接模块的简单方法 -- nn.Sequential
seq_model = nn.Sequential(
nn.Linear(1, 13),
nn.Tanh(),
nn.Linear(13, 1)
)
seq_model
Sequential(
(0): Linear(in_features=1, out_features=13, bias=True)
(1): Tanh()
(2): Linear(in_features=13, out_features=1, bias=True)
)
简单的分析下这个神经网络
- 第0层：线性层，输入为1
- 第1层：relu层
- 第2层，线性层，输出为1
#使用之前记得修改优化器
optimizer = optim.SGD(seq_model.parameters(), lr=1e-3)
#使用seq_model
train(
n_epochs = 5000,
optimizer = optimizer,
model = seq_model,
Loss = nn.MSELoss(),
X_train = X_train,
y_train = y_train,
X_val = X_val,
y_val = y_val)
Epoch 0, Training Loss 138.553635 Validation Loss 397
Epoch 500, Training Loss 7.982705 Validation Loss 59
Epoch 1000, Training Loss 3.104822 Validation Loss 31
Epoch 1500, Training Loss 2.151918 Validation Loss 21
Epoch 2000, Training Loss 1.641197 Validation Loss 16
Epoch 2500, Training Loss 1.356960 Validation Loss 13
Epoch 3000, Training Loss 1.198208 Validation Loss 11
Epoch 3500, Training Loss 1.105638 Validation Loss 10
Epoch 4000, Training Loss 1.050178 Validation Loss 9
Epoch 4500, Training Loss 1.016456 Validation Loss 8
# 可视化一下
fig = plt.figure(dpi=100)
plt.xlabel("X")
plt.ylabel("y")
y_pred = seq_model(X)
xx = torch.arange(2.0, 9.0, 0.1).unsqueeze(1)
plt.plot(xx.numpy(), seq_model(xx).detach().numpy(), 'c-')
plt.plot(X.numpy(), y_pred.detach().numpy(), 'kx')
plt.plot(X.numpy(), y.numpy(), 'o')
plt.show()
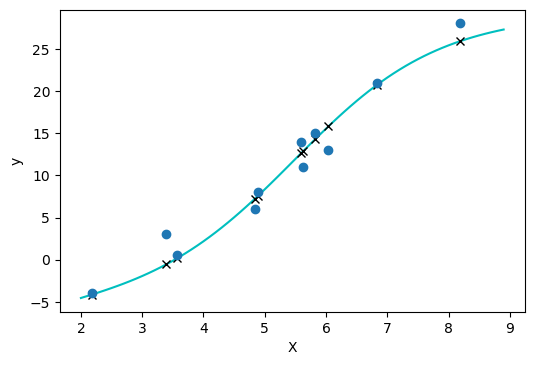
现在的曲线拟合看起来更好啦！ enjoy it!
参考
- 《Deep Learning with PyTorch》
- PyTorch中文文档
- PYTORCH DOCUMENTATION
