Adaboost算法及其代码实现

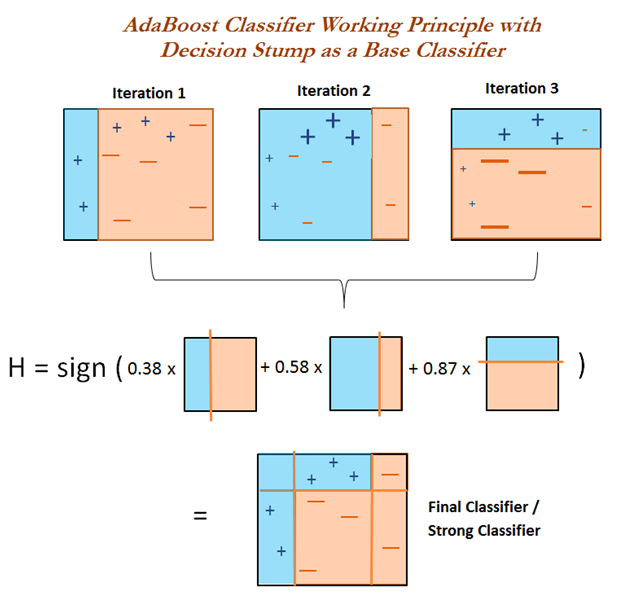
Adaboost算法及其代码实现

算法概述

AdaBoost（adaptive boosting），即自适应提升算法。

Boosting 是一类算法的总称，这类算法的特点是通过训练若干弱分类器，然后将弱分类器组合成强分类器进行分类。

为什么要这样做呢？因为弱分类器训练起来很容易，将弱分类器集成起来，往往可以得到很好的效果。

俗话说，"三个臭皮匠，顶个诸葛亮"，就是这个道理。

这类 boosting 算法的特点是各个弱分类器之间是串行训练的，当前弱分类器的训练依赖于上一轮弱分类器的训练结果。

各个弱分类器的权重是不同的，效果好的弱分类器的权重大，效果差的弱分类器的权重小。

值得注意的是，AdaBoost 不止适用于分类模型，也可以用来训练回归模型。

这需要将弱分类器替换成回归模型，并改动损失函数。

$几个概念

强学习算法：正确率很高的学习算法；
弱学习算法：正确率很低的学习算法，仅仅比随机猜测略好。

弱分类器：通过弱学习算法得到的分类器， 又叫基本分类器；
强分类器：多个弱分类器按照权值组合而成的分类器。

$提升方法专注两个问题：

1.每一轮如何改变训练数据的权值或者概率分布：

Adaboost的做法是提高被分类错误的训练数据的权值，而提高被分类错误的训练数据的权值。

这样，被分类错误的训练数据会得到下一次弱学习算法的重视。

2.弱组合器如何构成一个强分类器

加权多数表决。

每一个弱分类器都有一个权值，该分类器的误差越小，对应的权值越大，因为他越重要。

算法流程

给定二分类训练数据集：

$T = {(x_1, y_1), (x_2, y_2), ... , (x_n, y_n)}$
和弱学习算法

目标：得到分类器\(G(x)\)

1.初始化权重分布：

一开始所有的训练数据都赋有同样的权值，平等对待。

$D_1 = (w_{11}, w_{12}, ... , w_{1n})$, $w_{1i} = \frac{1}{N}$, $i = 1, 2, ... , N$
### 2.权值的更新 设总共有M个弱分类器，m为第m个弱分类器， $m = 1, 2, ... , M$ (1)第m次在具有$D_m$权值分布的训练数据上进行学习，得到弱分类器$G_m(x)$。 这个时候训练数据的权值：
$D_m = (w_{m, 1}, w_{m, 2}, ... , w_{m, n})$, $i = 1, 2, ... , N$
(2)计算$Gm(x)$在该训练数据上的**分类误差率**： 注：I函数单位误差函数
**分类误差率**：$e_m = \sum^{N}_{i = 1} w_i I (G_m(x_i) \neq y_i)$
(3)计算$G_(x)$的系数：
$\alpha_m = \frac 1 2 \ln \frac{1 - e_m}{e_m}$
(4)更新训练数据的权值：
$D_{m+1} = (w_{m+1, 1}, w_{m+1, 2}, ... , w_{m+1, n})$, $i = 1, 2, ... , N$
$w_{m+1, i} = \frac{w_{m, i}}{Z_m}\exp(-\alpha_m y_i G_m(x_i))$, $i = 1, 2, ... , N$
其中：
$Z_m = \sum^{N}_{i = 1} w_{m, i} \exp(-\alpha_m y_i G_m(x_i))$
正确的分类：$y_i G_m(x_i) = 1$
错误的分类：$y_i G_m(x_i) = -1$
### 3.构建基本分类器的线性组合 弱分类器乘以权重
$f(x) = \sum^{M}_{m = 1} \alpha_m G_m(x)$
最终分类器
$G_(x) = sign(f(x))$

一个例子

表 1. 示例数据集

第一轮迭代

1.a 选择最优弱分类器

第一轮迭代时，样本权重初始化为（0.167, 0.167, 0.167, 0.167, 0.167, 0.167）。

表1数据集的切分点有0.5, 1.5, 2.5, 3.5, 4.5

若按0.5切分数据，得弱分类器x < 0.5,则 y = 1; x > 0.5, 则 y = -1。此时错误率为2 * 0.167 = 0.334

若按1.5切分数据，得弱分类器x < 1.5,则 y = 1; x > 1.5, 则 y = -1。此时错误率为1 * 0.167 = 0.167

若按2.5切分数据，得弱分类器x < 2.5,则 y = 1; x > 2.5, 则 y = -1。此时错误率为2 * 0.167 = 0.334

若按3.5切分数据，得弱分类器x < 3.5,则 y = 1; x > 3.5, 则 y = -1。此时错误率为3 * 0.167 = 0.501

若按4.5切分数据，得弱分类器x < 4.5,则 y = 1; x > 4.5, 则 y = -1。此时错误率为2 * 0.167 = 0.334

由于按1.5划分数据时错误率最小为0.167，则最优弱分类器为x < 1.5,则 y = 1; x > 1.5, 则 y = -1。

1.b 计算最优弱分类器的权重

alpha = 0.5 * ln((1 – 0.167) / 0.167) = 0.8047

1.c 更新样本权重

x = 0, 1, 2, 3, 5时，y分类正确，则样本权重为：

0.167 * exp(-0.8047) = 0.075

x = 4时，y分类错误，则样本权重为：

0.167 * exp(0.8047) = 0.373

新样本权重总和为0.075 * 5 + 0.373 = 0.748

规范化后，

x = 0, 1, 2, 3, 5时，样本权重更新为：

0.075 / 0.748 = 0.10

x = 4时, 样本权重更新为：

0.373 / 0.748 = 0.50

综上，新的样本权重为(0.1, 0.1, 0.1, 0.1, 0.5, 0.1)。

此时强分类器为G(x) = 0.8047 * G1(x)。G1(x)为x < 1.5,则 y = 1; x > 1.5, 则 y = -1。则强分类器的错误率为1 / 6 = 0.167。

第二轮迭代

2.a 选择最优弱分类器

若按0.5切分数据，得弱分类器x > 0.5,则 y = 1; x < 0.5, 则 y = -1。此时错误率为0.1 * 4 = 0.4

若按1.5切分数据，得弱分类器x < 1.5,则 y = 1; x > 1.5, 则 y = -1。此时错误率为1 * 0.5 = 0.5

若按2.5切分数据，得弱分类器x > 2.5,则 y = 1; x < 2.5, 则 y = -1。此时错误率为0.1 * 4 = 0.4

若按3.5切分数据，得弱分类器x > 3.5,则 y = 1; x < 3.5, 则 y = -1。此时错误率为0.1 * 3 = 0.3

若按4.5切分数据，得弱分类器x < 4.5,则 y = 1; x > 4.5, 则 y = -1。此时错误率为2 * 0.1 = 0.2

由于按4.5划分数据时错误率最小为0.2，则最优弱分类器为x < 4.5,则 y = 1; x > 4.5, 则 y = -1。

2.b 计算最优弱分类器的权重

alpha = 0.5 * ln((1 –0.2) / 0.2) = 0.6931

2.c 更新样本权重

x = 0, 1, 5时，y分类正确，则样本权重为：

0.1 * exp(-0.6931) = 0.05

x = 4 时，y分类正确，则样本权重为：

0.5 * exp(-0.6931) = 0.25

x = 2,3时，y分类错误，则样本权重为：

0.1 * exp(0.6931) = 0.20

新样本权重总和为 0.05 * 3 + 0.25 + 0.20 * 2 = 0.8

规范化后，

x = 0, 1, 5时，样本权重更新为：

0.05 / 0.8 = 0.0625

x = 4时, 样本权重更新为：

0.25 / 0.8 = 0.3125

x = 2, 3时, 样本权重更新为：

0.20 / 0.8 = 0.250

综上，新的样本权重为(0.0625, 0.0625, 0.250, 0.250, 0.3125, 0.0625)。

此时强分类器为G(x) = 0.8047 * G1(x) + 0.6931 * G2(x)。G1(x)为x < 1.5,则 y = 1; x > 1.5, 则 y = -1。G2(x)为x < 4.5,则 y = 1; x > 4.5, 则 y = -1。按G(x)分类会使x=4分类错误，则强分类器的错误率为1 / 6 = 0.167。

第三轮迭代

3.a 选择最优弱分类器

若按0.5切分数据，得弱分类器x < 0.5,则 y = 1; x > 0.5, 则 y = -1。此时错误率为0.0625 + 0.3125 = 0.375

若按1.5切分数据，得弱分类器x < 1.5,则 y = 1; x > 1.5, 则 y = -1。此时错误率为1 * 0.3125 = 0.3125

若按2.5切分数据，得弱分类器x > 2.5,则 y = 1; x < 2.5, 则 y = -1。此时错误率为0.0625 * 2 + 0.250 + 0.0625 = 0.4375

若按3.5切分数据，得弱分类器x > 3.5,则 y = 1; x < 3.5, 则 y = -1。此时错误率为0.0625 * 3 = 0.1875

若按4.5切分数据，得弱分类器x < 4.5,则 y = 1; x > 4.5, 则 y = -1。此时错误率为2 * 0.25 = 0.5

由于按3.5划分数据时错误率最小为0.1875，则最优弱分类器为x > 3.5,则 y = 1; x < 3.5, 则 y = -1。

3.b 计算最优弱分类器的权重

alpha = 0.5 * ln((1 –0.1875) / 0.1875) = 0.7332

3.c 更新样本权重

x = 2, 3时，y分类正确，则样本权重为：

0.25 * exp(-0.7332) = 0.1201

x = 4 时，y分类正确，则样本权重为：

0.3125 * exp(-0.7332) = 0.1501

x = 0, 1, 5时，y分类错误，则样本权重为：

0.0625 * exp(0.7332) = 0.1301

新样本权重总和为 0.1201 * 2 + 0.1501 + 0.1301 * 3 = 0.7806

规范化后，

x = 2, 3时，样本权重更新为：

0.1201 / 0.7806 = 0.1539

x = 4时, 样本权重更新为：

0.1501 / 0.7806 = 0.1923

x = 0, 1, 5时, 样本权重更新为：

0.1301 / 0.7806 = 0.1667

综上，新的样本权重为(0.1667, 0.1667, 0.1539, 0.1539, 0.1923, 0.1667)。

此时强分类器为G(x) = 0.8047 * G1(x) + 0.6931 * G2(x) + 0.7332 * G3(x)。G1(x)为x < 1.5,则 y = 1; x > 1.5, 则 y = -1。G2(x)为x < 4.5,则 y = 1; x > 4.5, 则 y = -1。G3(x)为x > 3.5,则 y = 1; x < 3.5, 则 y = -1。按G(x)分类所有样本均分类正确，则强分类器的错误率为0 / 6 = 0。则停止迭代，最终强分类器为G(x) = 0.8047 * G1(x) + 0.6931 * G2(x) + 0.7332 * G3(x)。

代码实现

import numpy as np

X = np.arange(6)
y = np.array([1, 1, -1, -1, 1, -1])


class my_adabosot(object):
    """docstring for my_adabosot"""

    def __init__(self, max_iter=3):
        super(my_adabosot, self).__init__()
        self.max_iter = max_iter

    def fit(self, X, y):
        self.X = X
        self.y = y
        self.clf_list = []
        self.cut_list = self.cut_list() # 例子中换成[0.5, 1.5, 2.5, 3.5, 4.5]
        self.w = np.ones(len(X)) / len(X)  # 最初的权重

        for i in range(self.max_iter):
            loss_list = []
            for a_index in self.cut_list:
                loss_list.append(sum(self.w[self.G_(self.X, a_index) != self.y]))

            loss_array = np.array(loss_list)
            a_index = np.argmin(loss_array)
            a = self.cut_list[a_index]
            em = np.sum(np.min(loss_array))
            alpha = 1 / 2 * np.log(1 / em - 1)
            alpha = np.round(alpha, 4)
            self.clf_list.append([alpha, a])

            # 更新参数
            temp_array = -alpha * self.y * self.G_(self.X, a_index)
            Zm = np.dot(self.w, np.exp(temp_array))
            #print(self.w)
            self.w = self.w / Zm * np.exp(temp_array)



    def predict(self, X):
        res = []
        for i in range(X):
            temp = 0
            for clf in self.clf_list:
                temp += clf[0] * G_(X, clf[1])
                res.append(-1 if temp > 0 else 1)

        return  np.array(res)


    def G_(self, X, a):
        Z = np.zeros(len(self.X))
        Z[X > a] = -1
        Z[X <= a] = 1
        return Z


    def cut_list(self):
        return  np.arange(self.X.min(), self.X.max(), 0.5)

clf = my_adabosot()
clf.fit(X, y)
#print(clf.cut_list)
for alpha in clf.clf_list:
    print(alpha)

Adaboost的另一种解释

Adaboost算法也可以认为是特殊的加法模型：损失函数为指数函数，学习算法为前向分布算法
加法模型

\[f(x) = \sum^{M}_{m=1} \beta_m b(x; \gamma_m) \]

其中：
\(b(x; \gamma_m)\)是基函数，可以是多项式函数；
\(\gamma_m\)是基函数的参数，即多项式的各项权值；
\(\beta_m\)是基函数的系数，即基函数的加权系数。

在给定的损失函数\(L(y, f(x))\)下，学习加法模型\(f(x)\)成为损失函数最小化问题。

\[\min_{\beta_m, \gamma_m} \sum^{N}_{i=1}L(y_i, \sum^{M}_{m=1}\beta_m b(x; \gamma_m)) \]

posted @ 2020-01-30 00:16  hichens  阅读(1846)  评论(1)  编辑  收藏  举报