leetcode hot 100-42. 接雨水
42. 接雨水
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。
示例1：
输入：height = [0,1,0,2,1,0,1,3,2,1,2,1] 输出：6 解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。
示例 2：
输入：height = [4,2,0,3,2,5] 输出：9
提示：
n == height.length 0 <= n <= 3 * 104 0 <= height[i] <= 105
思路参考：https://leetcode-cn.com/problems/trapping-rain-water/solution/jie-yu-shui-by-leetcode/
思路一：暴力法
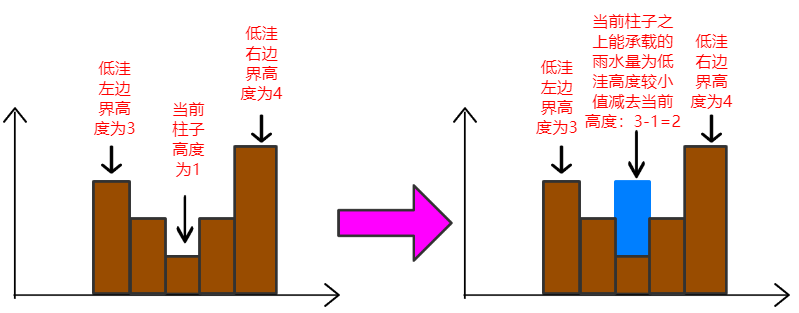
思路概括：求出当前柱子在所处最大低洼中能存储多少水，对所有柱子求出该柱子之上能存储的水量之后累加起来就是最终的结果
具体实现过程：
遍历每个柱子，对每个柱子进行下面的操作：
遍历左边所有柱子，找到所有柱子的最大值，即找到低洼的左边界；
遍历右边所有柱子，找到所有柱子的最大值，即找到低洼的右边界；
因为木桶能装多少水取决于最短的那块木板，低洼能装多少水取决于左右边界的较小者。左右边界的较小值即使当前低洼的水平面的高度h，当前柱子已有height[i]高度，所以在这个柱子之上还能存储（低洼高度-当前柱子高度）单位的水
1 class Solution { 2 public int trap(int[] height) { 3 4 int res = 0; 5 int len = height.length; 6 for(int i = 0; i < len; i++){ 7 int leftMax = height[i], rightMax = height[i]; // 低洼的左右边界均初始化为当前高度 8 for(int j = i - 1; j >= 0; j--){ // 到左边所有柱子的最大值，即找到低洼的左边界 9 leftMax = Math.max(leftMax, height[j]); 10 } 11 for(int j = i + 1; j < len; j++){ // 到右边所有柱子的最大值，即找到低洼的右边界 12 rightMax = Math.max(rightMax, height[j]); 13 } 14 // 左右边界较小者即是低洼水平面的高度，低洼高度减去柱子高度等于柱子之上还能存储的水量 15 res += Math.min(leftMax, rightMax) - height[i]; 16 } 17 return res; 18 } 19 }
leetcode 执行用时：90 ms > 6.62%的用户; 内存消耗：38.3 MB, 在所有 Java 提交中击败了76.41%的用户
复杂度分析：
时间复杂度：O(n)。很明显有双重循环，外层循环遍历了每个元素，内层循环迭代次数之和也是数组长度，所以时间复杂度为O(n)。
空间复杂度：O(1)。只需要常数个变量的空间。
思路二：动态编程
思路和刚才一样，也是计算出每个柱子在所处低洼的水平面后与柱子高度做差。但是这里采用先用数组把每个柱子所处低洼的左右边界记录下来的方式，减少内部的循环，将时间复杂度降低为O(n)。
最后遍历数组， 根据每个柱子的左右边界以及柱子本身的高度，计算出这个柱子能承受的水量
1 class Solution { 2 public int trap(int[] height) { 3 4 if(height == null || height.length == 0){ 5 return 0; 6 } 7 8 int len = height.length; 9 // 先用数组把每个柱子所处低洼的左右边界记录下来 10 int[] maxLeft = new int[len]; 11 int[] maxRight = new int[len]; 12 maxLeft[0] = height[0]; 13 for(int i = 1; i < len; i++){ // 计算每个主机所处低洼的左边界 14 maxLeft[i] = Math.max(maxLeft[i-1], height[i]); 15 } 16 17 maxRight[len - 1] = height[len - 1]; 18 for(int i = len - 2; i >= 0; i--){ // 计算每个主机所处低洼的右边界 19 maxRight[i] = Math.max(maxRight[i+1], height[i]); 20 } 21 22 // 最后遍历数组， 根据每个柱子的左右边界以及柱子本身的高度，计算出这个柱子能承受的水量 23 int res = 0; 24 for(int i = 0; i < len; i++){ 25 res += Math.min(maxLeft[i], maxRight[i]) - height[i]; 26 } 27 return res; 28 } 29 }
leetcode 执行用时：1 ms, 在所有 Java 提交中击败了99.99%的用户, 可以看到这个时间花费明显小于思路一
内存消耗：38.1 MB, 在所有 Java 提交中击败了87.78%的用户
复杂度分析：
时间复杂度：O(n)。只有三个并列的 for 循环，所以时间复杂度为O(n)。
空间复杂度：O(2n)。需要2个大小为 n 的临时数组， 所以空间复杂度为O(2n)。
思路三：双指针法
双指针法，每次比较左右柱子的大小，
如果左柱子低于右柱子，说明存在比左柱子高的右边界，左柱子可能处于某个低洼，可以进一步判断左边界与它的关系，决定是否能够承载水量
- 计算左柱子能承受的水量
- 如果左边界低于当前柱子，说明左柱子处于水平面之上，不能承载水量，这时应该更新左边界的高度，并把左指针向中间移一位，计算下个柱子能承受的水量。
如果左柱子高于于右柱子，说明存在比右柱子高的左边界，右柱子可能处于某个低洼，可以进一步判断右边界与它的关系，决定右柱子是否能够承载水量
- 如果右边界高于右柱子，说明右柱子处于水平面之下，计算右柱子能承受的水量
- 如果右边界低于右柱子，说明右柱子处于水平面之上，不能承载水量，这时应该更新右边界的高度，并把右指针向中间移一位，计算下个柱子能承受的水量。
等左右指针相撞，说明已经把所有的柱子都遍历了一遍，每个柱子的能承受的水量都已经求出来了，跳出循环。
1 class Solution { 2 public int trap(int[] height) { 3 4 if(height == null || height.length == 0){ 5 return 0; 6 } 7 8 int len = height.length; 9 int leftMax = 0; 10 int rightMax = 0; 11 int res = 0; 12 int left = 0, right = len - 1; 13 while(left <= right){ 14 // 左柱子低于右柱子，说明左柱子的右边界高于它，可以进一步判断左边界与它的关系 15 if(height[left] < height[right]){ 16 if(height[left] <= leftMax){ // 如果左边界高于当前柱子，说明当前柱子处于水平面之下 17 res += leftMax - height[left]; 18 }else{ // 如果左边界低于当前柱子，说明当前柱子处于水平面之上，不能承载水量 19 leftMax = height[left]; 20 } 21 left++; 22 }else{ // 左柱子高于右柱子，说明存在比右柱子高的左边界，可以进一步判断右边界与它的关系 23 if(height[right] <= rightMax){ // 如果右边界高于当前柱子，说明当前柱子处于水平面之下 24 res += rightMax - height[right]; 25 }else{ // 如果右边界高于当前柱子，说明当前柱子处于水平面之上，不能承载水量 26 rightMax = height[right]; 27 } 28 right--; 29 } 30 } 31 return res; 32 } 33 }
leetcode 执行用时：1 ms, 在所有 Java 提交中击败了99.99%的用户;
内存消耗：38.3 MB, 在所有 Java 提交中击败了75.15%的用户
复杂度分析：
时间复杂度：O(n)。两个指针加起来对所有的柱子遍历了一次，所以时间复杂度为O(n)。
空间复杂度：O(1)。只需要常数个变量的空间。
思路四：单调栈：
此算法的实现思路和上面三种算法的实现思路不一样，上面三种思路都是对于当前柱子找到该柱子的全局左右边界，得出水平面的高度，从而得出当前柱子能承载的水量。思路4则采用的是找到局部的左右边界，计算局部的低洼容量，所有局部低洼容量即是总的能存储的雨水量。
思路概括：
遍历 height数组，维护一个从栈底到栈顶递减序列的单调栈，当碰到待入栈柱子高度高于栈顶下标对应的柱子时，弹出栈顶下标, 假定该下标为top, 求出以该下标对应的柱子为底（低洼的河床），分别以此时栈顶下标对应柱子和current所指柱子为左右边界的低洼的容量。
具体实现如下：栈不为空且当前柱子高于栈顶下标对应的柱子，说明栈顶下标对应的柱子找到了一个右边界。此时
- 出栈栈顶下标
- 判断栈是否为空，如果栈为空，说明左边界为0， 该柱子不能承载水量，跳出该循环，
- 如果栈不为空，说明该柱子存在左边界，且因为栈是递减栈，栈内元素对应的的柱子高度一定不矮于该柱子，所以该柱子存在一个不矮于自己的左边界，所以可以承载一定的水量
- 计算左右边界的下标之差减一，即是该柱子当前低洼的宽度；
- 左右边界的高度较小者即是低洼的水平面，水平面减去柱子高度即是该低洼的深度，该柱子的表面即是低洼的河床；
- 根据低洼的深度和宽度，两者相乘得到了该低洼能承载的水量
循环出栈，直至栈为空或者当前柱子高于栈顶下标对应的柱子，说明栈顶下标对应的柱子找到了一个右边界
入栈当前柱子下标,并且让 current 后移一位使得 current 指向下个柱子
1 class Solution { 2 public int trap(int[] height) { 3 4 int len = height.length; 5 Stack<Integer> stack = new Stack<>(); // 单调栈，栈底到栈顶递减 6 int current = 0; 7 int res = 0; // 存储结果水量 8 while(current < len){ 9 // 栈不为空且当前柱子高于栈顶下标对应的柱子，说明栈顶下标对应的柱子找到了一个右边界 10 while(!stack.isEmpty() && height[current] > height[stack.peek()]){ 11 // 弹出栈顶下标 12 int top = stack.pop(); 13 // 判断栈是否为空，如果栈为空，说明左边界为0， 该柱子不能承载水量，跳出该循环， 14 if(stack.isEmpty()){ 15 break; 16 } 17 // 计算左右边界的下标之差减一，即使该柱子当前低洼的宽 18 int width = current - stack.peek() - 1; 19 // 左右边界的高度较小者即是低洼的水平面， 20 // 水平面减去柱子高度即是该低洼的深度，该柱子的表面即是低洼的河床； 21 int bottom = Math.min(height[current], height[stack.peek()]) - height[top]; 22 // 根据低洼的深度和宽度，两者相乘得到了该低洼能承载的水量 23 res += width * bottom; 24 } 25 // 入栈当前柱子下标,并且让 current 后移一位使得 current 指向下个柱子 26 stack.push(current++); 27 } 28 return res; 29 } 30 }
leetcode 执行用时：4 ms, 在所有 Java 提交中击败了28.77%的用户
内存消耗：38.3 MB, 在所有 Java 提交中击败了77.37%的用户
复杂度分析：
时间复杂度：O(n)。每个柱子下标最多入栈和出栈一次，所以算法的时间复杂度为O(n)。
空间复杂度：O(n)。需要一个栈，这个栈是个递减栈，栈的元素个数最多为O(n),即当height[ ]数组本身是个递减数组时，所有元素的下标均会被入栈。
