动态规划 ---- 最长回文子串

分析:

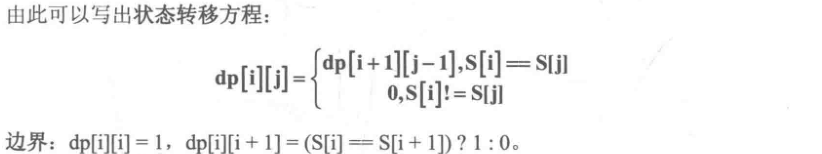
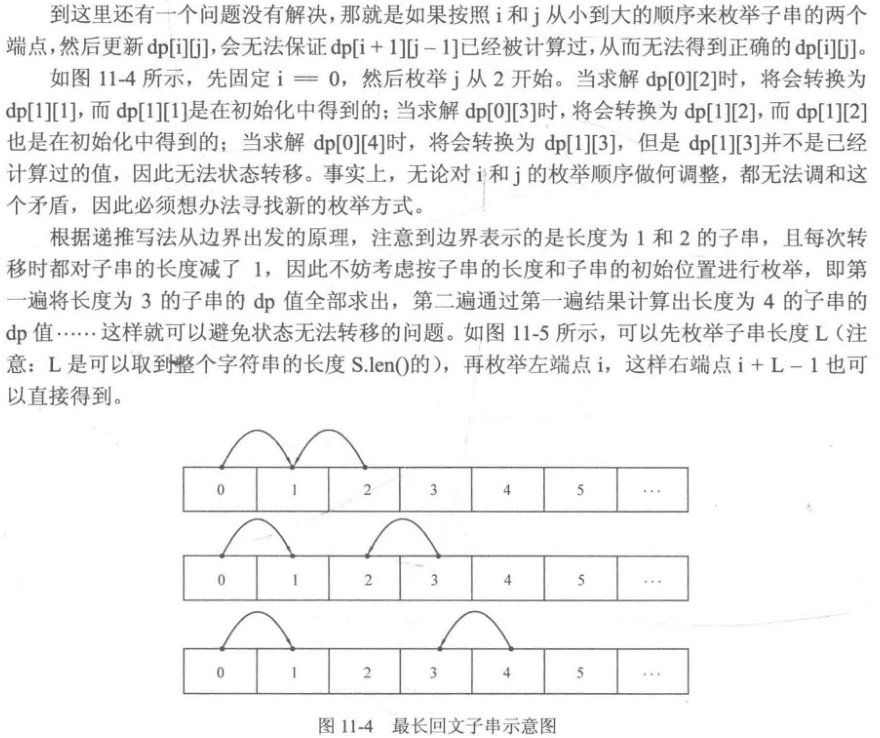
完整代码:
C++实现
1 #include <stdio.h> 2 #include <iostream> 3 #include <cstring> 4 using namespace std; 5 6 const int maxn = 1010; 7 char S[maxn]; 8 int dp[maxn][maxn]; 9 10 int main() 11 { 12 cin.getline(S, 1010); 13 int len = strlen(S), ans = 1; 14 memset(dp, 0, sizeof(dp)); // dp数组初始化为0 15 // 边界 16 for (int i = 0; i < len; i++){ 17 dp[i][i] = 1; 18 if (i < len - 1){ 19 if (S[i] == S[i + 1]){ 20 dp[i][i + 1] = 1; 21 ans = 2; // 初始化是注意当前最长回文子串长度 22 } 23 } 24 } 25 // 状态转移方程 26 for (int L = 3; L <= len; L++){ // 枚举子串的长度 27 for (int i = 0; i + L - 1 < len; i++){ // 枚举子串的起始端点 28 int j = i + L - 1; // 子串的右端点 29 if (S[i] == S[j] && dp[i + 1][j - 1] == 1){ 30 dp[i][j] = 1; 31 ans = L; // 更新最长回文子串的长度 32 } 33 } 34 } 35 36 printf("%d\n", ans); 37 38 return 0; 39 }
Java实现
1 class Solution { 2 public int[][] dp; 3 4 public String longestPalindrome(String s) { 5 // 令dp[i][j]表示s[i]到s[j]之间的字符是否是回文串 6 // 当s[i+1] == s[j-1]时dp[i][j] = 1 7 // 否则dp[i][j] = 0; 8 // 初始化dp[i][i] = 1和dp[i][i+1] = (s[i]==s[j]) ? 1:0 9 // 依次照度长度为3,4...L的回文子串 10 int len = s.length(); 11 12 dp = new int[len][len]; 13 for(int i = 0; i < len; i++){ 14 Arrays.fill(dp[i], 0); 15 } 16 // 初始化dp数组的边界 17 int ans = 1; // 存储最大回文串的长度 18 for(int i = 0; i < len; i++){ 19 dp[i][i] = 1; 20 if(i < len - 1){ 21 if(s.charAt(i) == s.charAt(i+1)){ 22 dp[i][i+1] = 1; 23 ans = 2; 24 } 25 26 } 27 } 28 29 // 从长度为3开始递增长度按转态转移方程给dp数组赋值 30 for(int L = 3; L <= len; L++){ 31 for(int i = 0; i + L - 1< len; i++){ 32 int j = i + L - 1; 33 if(s.charAt(i) == s.charAt(j) && dp[i+1][j-1] == 1){ 34 dp[i][j] = 1; 35 ans = L; 36 } 37 } 38 } 39 40 // 扫描一次dp[i][j] 41 // 寻找第一个等于dp[i][j] == ans的值 42 for(int i = 0; i + ans - 1 < len; i++){ 43 for(int j = i + ans - 1; j < len; j++){ 44 if(1 == dp[i][j]){ 45 return s.substring(i, j + 1); 46 } 47 } 48 } 49 return ""; 50 } 51 }
复杂度分析:
时间花费有三部分,① 对dp[][]赋边界值,所需时间为O(n), ② 从长度为3开始递增长度按转态转移方程给dp数组赋值,可以看到有一个双重循环,所需时间为O(n^2) ③ 找到第一个长度为L的回文子串,所需时间为O(n), 所以总的时间复杂度为O(n^2).
空间复杂度则是一个二维数组的空间,复杂度为O(n^2)


