《动手学强化学习》笔记
Multi-Armed Bandit
伯努利Multi-Armed Bandit
import numpy as np # 支持数组和矩阵运算的库
import matplotlib.pyplot as plt # 绘图库
class BernoulliBandit: # K-Armed Bandit
"""伯努利Multi-Armed Bandit,输入k表示拉杆个数"""
def __init__(self, K):
self.probs = np.random.uniform(size=K) # 随机生成K个小数,作为从杆1到杆K的获奖概率
self.best_idx = np.argmax(self.probs) # 获奖概率最大的拉杆
self.best_prob = self.probs[self.best_idx] # 最大的获奖概率
self.K = K
def step(self, k): # 拉动拉杆k 返回:获得获奖1,不获奖0
if np.random.rand() < self.probs[k]: # 比方说杆3获奖概率为0.7,我们此时抽出了0.6,就代表获奖了,从几何概型的角度思考
return 1
else:
return 0
np.random.seed(1) # 设置种子,保证结果的可重复性
K = 10
bandit_10_arm = BernoulliBandit(K)
print(type(bandit_10_arm.probs))
print(type(bandit_10_arm.best_idx))
print(type(bandit_10_arm.best_prob))
print(bandit_10_arm.best_idx) # 最大获奖的杆编号
print(bandit_10_arm.best_prob) # 最大获奖概率
运行结果:
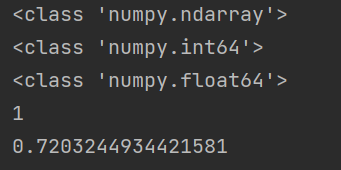
probs 的类型为ndarray,是NumPy库的一个数据类型,表示N维数组
解决MAB问题
# 定义完MAB对象后:
# 二项分布的期望:NP
# 求解MAB问题:
class Solver:
"""MAB基本框架"""
def __init__(self, bandit): # bandit: 为上面一个MAB的类对象
self.bandit = bandit
self.counts = np.zeros(self.bandit.K) # counts:每根拉杆的尝试次数,初始化为0
self.regret = 0. # 当前步的累计懊悔
self.actions = [] # 列表,记录每一步的动作(拉哪一根杆)
self.regrets = [] # 列表,记录每一步的累计懊悔
def update_regret(self, k):
"""更新累计懊悔并且保存,k为本次动作选择的拉杆的编号"""
self.regret += self.bandit.best_prob - self.bandit.probs[k] # 选择一个杆然后拉,考察获奖情况,等于是对这个杆进行了一次伯努利
# 实验,所有拉动一个杆获得奖励的期望就为 1 * prob[i]
self.regrets.append(self.regret)
def run_one_step(self): # 根据策略选择动作、根据动作获取奖励和更新期望奖励估值
# 返回当前动作选择哪一根拉杆,由每个具体策略进行实现
raise NotImplementedError
def run(self, num_steps): # 更新累积懊悔和计数
# 运行一定次数,num_steps为总运行次数
for _ in range(num_steps):
k = self.run_one_step() # k 为选择杆的编号
self.counts[k] += 1
self.actions.append(k)
self.update_regret(k)
import numpy as np # 支持数组和矩阵运算的库
import matplotlib.pyplot as plt # 绘图库
# 生成MAB:
class BernoulliBandit: # K-Armed Bandit
"""伯努利Multi-Armed Bandit,输入k表示拉杆个数"""
def __init__(self, K):
self.probs = np.random.uniform(size=K) # 随机生成K个小数,作为从杆1到杆K的获奖概率
self.best_idx = np.argmax(self.probs) # 获奖概率最大的拉杆
self.best_prob = self.probs[self.best_idx] # 最大的获奖概率
self.K = K
def step(self, k): # 拉动拉杆k 返回:获得获奖1,不获奖0
if np.random.rand() < self.probs[k]: # 比方说杆3获奖概率为0.7,我们此时抽出了0.6,就代表获奖了,从几何概型的角度思考
return 1
else:
return 0
np.random.seed(1) # 设置种子,保证结果的可重复性
K = 10
bandit_10_arm = BernoulliBandit(K)
print(type(bandit_10_arm.probs))
print(type(bandit_10_arm.best_idx))
print(type(bandit_10_arm.best_prob))
print(bandit_10_arm.best_idx) # 最大获奖的杆编号
print(bandit_10_arm.best_prob) # 最大获奖概率
# 二项分布的期望:NP
# 求解MAB问题:
class Solver:
"""MAB基本框架"""
def __init__(self, bandit): # bandit: 为上面一个MAB的类对象
self.bandit = bandit
self.counts = np.zeros(self.bandit.K) # counts:每根拉杆的尝试次数,初始化为0
self.regret = 0. # 当前步的累计懊悔
self.actions = [] # 列表,记录每一步的动作(拉哪一根杆)
self.regrets = [] # 列表,记录每一步的累计懊悔
def update_regret(self, k):
"""更新累计懊悔并且保存,k为本次动作选择的拉杆的编号"""
self.regret += self.bandit.best_prob - self.bandit.probs[k] # 选择一个杆然后拉,考察获奖情况,等于是对这个杆进行了一次伯努利
# 实验,所有拉动一个杆获得奖励的期望就为 1 * prob[i]
self.regrets.append(self.regret)
def run_one_step(self): # 根据策略选择动作、根据动作获取奖励和更新期望奖励估值
# 返回当前动作选择哪一根拉杆,由每个具体策略进行实现
raise NotImplementedError
def run(self, num_steps): # 更新累积懊悔和计数
# 运行一定次数,num_steps为总运行次数
for _ in range(num_steps):
k = self.run_one_step() # k 为选择杆的编号
self.counts[k] += 1
self.actions.append(k)
self.update_regret(k)
# MAB解决方法1:Epsilon贪婪算法
class EpsilonGreedy(Solver):
"""继承自Solver类"""
def __init__(self, bandit, epsilon=0.01, init_prob=1.0): # bandit:一个MAB对象,探索的概率
super(EpsilonGreedy, self).__init__(bandit)
self.epsilon = epsilon
self.estimates = np.array([init_prob] * self.bandit.K) # 初始化拉动所有拉杆的期望奖励估值
def run_one_step(self):
if np.random.random() < self.epsilon: # 进行探索
k = np.random.randint(0, self.bandit.K) # 随机选择一个杆k
else:
k = np.argmax(self.estimates) # 不进行探索,而是选择当前的最优期望
r = self.bandit.step(k) # 本次动作的奖励,也就是获奖或者不获奖
self.estimates[k] += 1. / (self.counts[k] + 1) * (r - self.estimates[k]) # 更新杆k的当前期望
return k
# 生成累计懊悔随时间变化的图像
def plot_results(solvers, solver_names): # solvers: 列表,列表中每个元素是一种特定的策略, solver_names: 列表,存储每个策略的名称
for idx, solver in enumerate(solvers): # enumerate 会同时返回列表里面的序列和元素,跟map差不多: 0, Spring; 1, Summer 等
time_list = range(len(solver.regrets))
plt.plot(time_list, solver.regrets, label=solver_names[idx])
plt.xlabel('Time steps')
plt.ylabel('Cumulative regrets')
plt.title('%d-armed bandit' % solvers[0].bandit.K)
plt.legend()
plt.show()
# 测试贪婪算法并画图
np.random.seed(1)
epsilon_greedy_solver = EpsilonGreedy(bandit_10_arm)
epsilon_greedy_solver.run(5000)
print('epsilon-贪婪算法的累积懊悔为:', epsilon_greedy_solver.regret)
plot_results([epsilon_greedy_solver], ["EpsilonGreedy"])
# 随时间衰减的贪婪算法
class DecayingEpsilonGreedy(Solver):
def __init__(self, bandit, init_probs=1.0):
super(DecayingEpsilonGreedy, self).__init__(bandit)
self.estimates = np.array([init_probs] * self.bandit.K)
self.total_count = 0
def run_one_step(self):
self.total_count += 1
if np.random.random() < 1 / self.total_count: # epsilon 随时间衰减
k = np.random.randint(0, self.bandit.K)
else:
k = np.argmax(self.estimates)
r = self.bandit.step(k)
self.estimates[k] += 1. / (self.counts[k] + 1) * (r - self.estimates[k])
return k
np.random.seed(1)
decaying_epsilon_greedy_solver = DecayingEpsilonGreedy(bandit_10_arm)
decaying_epsilon_greedy_solver.run(5000)
print('epsilon 值衰减的贪婪算法的累计懊悔为:', decaying_epsilon_greedy_solver.regret)
plot_results([decaying_epsilon_greedy_solver],["DecayingEpsilonGreedy"])
reversed用法
def compute_return(start_index, chain, gamma):
G = 0 # 回报
for i in reversed(range(start_index, len(chain))):
G = gamma*G + rewards[chain[i] - 1]
return G
这段代码出自:动手学强化学习, 中,计算回报的代码,其中,reversed的作用是将range(a, b)生成的区间[a,b), 反转成(b,a], 等价于C++:
for(int i = b - 1; i >= a; i--)
如:

字典中get函数的用法
字典:
p = {
"我": 1
"你":2
}
就是字典
p.get(“我”, 0)

np.zeros([行数,列数])
用法如下:

np.random.random(size) 用法
随机返回数据规模为size的数,这些数均在[0, 1]之间:

collections.deque()
参考
collections 是python的一个数据结构库, 常用的模块有:
deque:双向队列
Counter:计数器
defaultdict:默认字典
OrderedDict:有序字典
deque()
deque是栈和队列的一种广义实现,deque是"double-end queue"的简称;deque支持线程安全、有效内存地以近似O(1)的性能在deque的两端插入和删除元素,尽管list也支持相似的操作,但是它主要在固定长度操作上的优化,从而在pop(0)和insert(0,v)(会改变数据的位置和大小)上有O(n)的时间复杂度。
常用方法:
append()
末端添加元素
appendleft()
前端添加元素
extend()
末端逐个添加可迭代对象

extendleft()
前端逐个添加可迭代对象
pop()
移除队列的一个元素,默认最右端的一个元素,并返回该元素的值
popleft()
移除队列的一个元素,默认最左端的一个元素,并返回该元素的值
count(x)
统计队列中x元素的个数

insert(index, obj)
在位置index插入元素obj

len(tensor) 与 tensor.shape:
- len(tensor) 返回tensor的第零维的维数,如果只有两维,那么第零维为行数
- tensor.shape 返回一个一行n列的tensor,分别为tensor的每一维的维度

浅析kmeans_torch库中的initialize与距离函数:
import torch
import numpy as np
def initialize(X: torch.Tensor, num_clusters: int) -> torch.Tensor:
"""
选出中心点
initialize cluster centers
:param X: (torch.tensor) matrix
:param num_clusters: (int) number of clusters
:return: (np.array) initial state
"""
num_samples = len(X) # X的行数
indices = np.random.choice(num_samples, num_clusters, replace=False)
# 从num_samples(一维) 中随机不重复
# 取num_clusters个数,组成一个一维array —— indices
initial_state = X[indices] # 将X的indices这些行取出来,作为一个新的tensor
return initial_state
def pairwise_distance(data1, data2, device=torch.device('cpu')):
# transfer to device
data1, data2 = data1.to(device), data2.to(device)
# N1*1*M
A = data1.unsqueeze(dim=1)
# 1*N2*M
B = data2.unsqueeze(dim=0)
# 因为有上面两个unsqueeze操作,使得A中的每一行变为单独一个维度,然后对应全部的B,利用广播机制进行减法运算
# 最后A-B返回一个N1*N2*M的tensor
dis = (A - B) ** 2.0 # 点乘:对应位置分别相乘,仍然为一个N1*N2*M的tensor
# return N1*N2 matrix for pairwise distance
# 倒数第一维度:最内层的维度:M维(2维)彼此相加,这个squeeze()貌似没作用
dis = dis.sum(dim=-1).squeeze()
return dis # 返回一个N1*N2的tensor,每一行分别代表某点对N2个中心点的距离的平方和
data_size, dims, num_clusters = 10, 2, 3
x = np.random.randn(data_size, dims) / 10 # 除以10是为了缩小数值,方便画图
x = torch.from_numpy(x)
print(x)
b = initialize(x, 3)
print(b)
结果:

x共10行表示10个点,每行两列,分别表示横坐标和纵坐标
b 为x中随机选取的3个点
经过unsqueeze操作
观察求距离的代码,发现有unsqueeze操作,如果没有这个操作,那么tensor x与b由于维数不同而没法用广播机制且没法进行减法运算
经过unsqueeze后,可以近似认为,x中的每一行成了一维,b整个成了一维,然后x-b就可以利用广播机制进行运算:

x-b就是10*3*2的tensor

然后又进行了sum操作:
对dim=-1进行sum,就等价于对dim=2进行sum,也就是M维度
测试:
c = x - b
print(c.shape)
c = c.sum(dim=-1)
print(c.shape)
print(c)
c = c.squeeze()
print(c)
print(c.shape)
结果:

torch.nonzero() 的用法:
里面传tensor:
返回该tensor中所有非零元素的下标,具体见文章
里面传bool表达式:
如kmeans_pytorch包中:

这里返回的是所有使得布尔表达式成立的元素的索引:





