最短路径-Dijkstra算法，以洛谷P4779 【模板】单源最短路径（标准版）为例

Dijkstra算法

条件

处理 图 的单源最短路且边权均为非负的情况

例题和代码

例题

链接：洛谷P4779

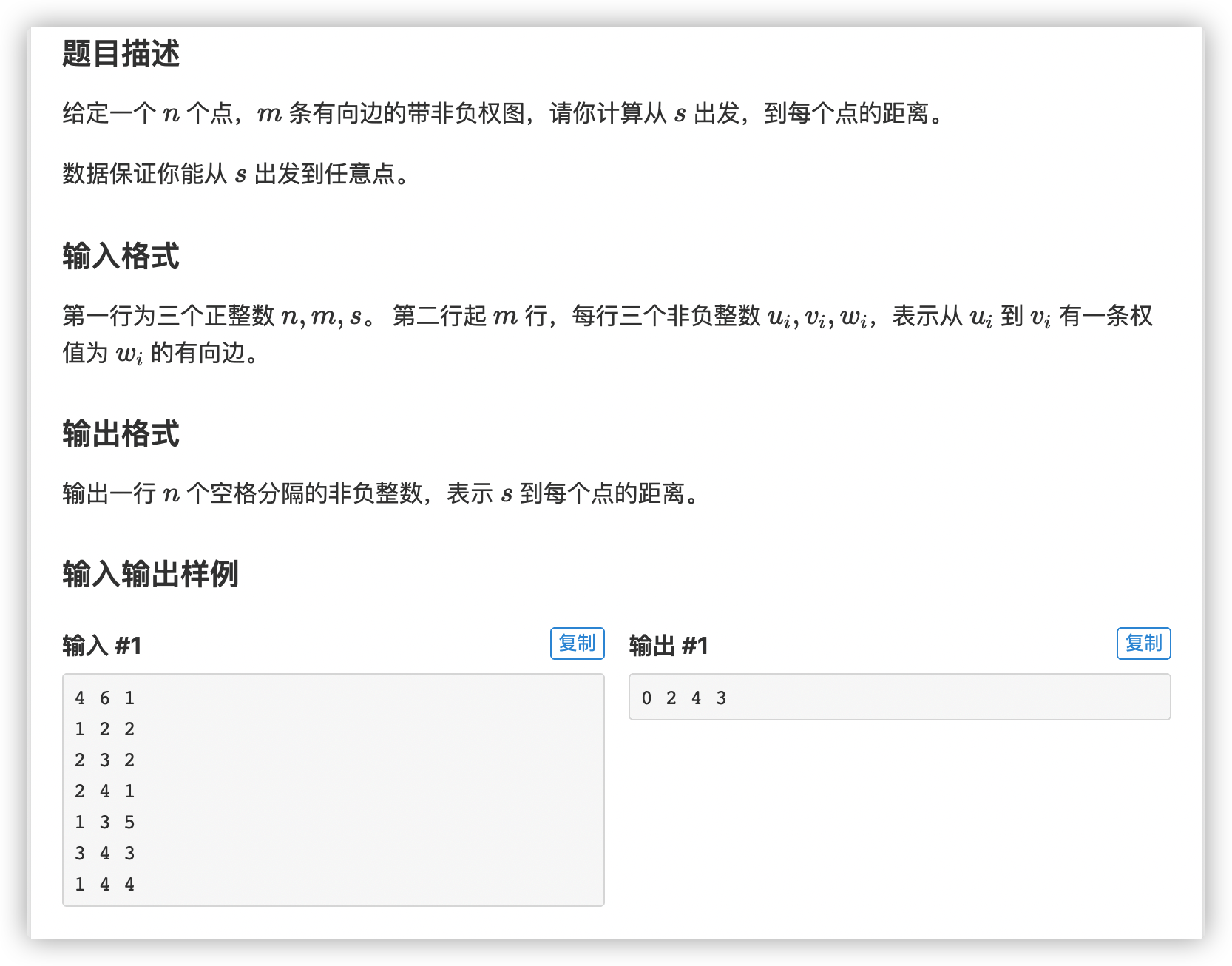
代码

/*
 * 将所有路径以二元组（路径长度，终点）的形式放入以路径长度为关键字的小根堆中，每次取出堆顶元素，查看该终点是否已确定最短路。同时删除堆顶。
 *（1）已确定 则不做处理
 *（2）未确定，确定该点最短路，并进行松弛操作：遍历该点所有出边，查看是否能更新相邻点的最短路，若产生更新则将新的最短路加入堆。
 * 一直处理到堆为空则所有点的最短路均被确定。
 */

/*
 * 采用 边集 和 链式前向星 的方法来记录 图
 */

#include <iostream>
#include <algorithm>
#include <queue>

#define N 200005 // 共有1e5个点
using namespace std;

int n, m, rt, dis[N], l_id, head[N];
// n 个点，m 条路径，均为有向非负权，rt 原点是哪一个
// dis 用来存储每个点的最短路，dis数组开始时候会被赋值为无穷大
// l_id 和 head 均是用来实现存边操作的数组，l_id 为边的id  （边集和链式前向星）

// 用边集来存储边
// head[u] 的含义是一条从 u 射出的边的编号. id， 则 Edge[id] 编号为id的那条边
// edge[i].to表示第i条边的终点,edge[i].next表示与第i条边同起点的下一条边的存储位置,edge[i].w为边权值
struct EDGE
{ // 存边的结构体
    int to, next, vlu;
    // to: 去哪个点 next 下一条边 ，vlu 这条边的权重
} Edge[N];

void add(int u, int v, int vlu)
{ // 添加边，表示从 u 到 v 的一条权值为 vlu 的边
    Edge[++l_id].to = v;
    Edge[l_id].next = head[u];
    head[u] = l_id;
    Edge[l_id].vlu = vlu;
}

const int MAXN = 2e9;
bool vis[N]; // 标记第N个点是否已经找到最短距离

struct node
{ //结构体用来存放二元组，这个二元组是 终点，路径长度（权重）
    // id 该二元组指向的终点是哪一个，vlu 这条路径的长度（权重）
    int id, vlu;
};

bool operator<(node x, node y)
{ // 重载运算符，将小于号变为大于号，使得后续可以将STL中的大根堆变为小跟堆
    return x.vlu > y.vlu;
}

int main()
{
    scanf("%d%d%d", &n, &m, &rt);
    for (int i = 1; i <= n; i++)
        dis[i] = MAXN;
    for (int i = 1; i <= m; i++)
    {
        int x, y, v;
        scanf("%d%d%d", &x, &y, &v);
        add(x, y, v);
    }
    priority_queue<node> q; // 小跟堆
    q.push((node){rt, 0});
    dis[rt] = 0;
    while (!q.empty())
    {
        node x = q.top();
        q.pop();
        if (vis[x.id])
            continue;
        vis[x.id] = 1;
        for (int i = head[x.id]; i; i = Edge[i].next)
        {
            int v = Edge[i].to;
            if (vis[v])
                continue;
            if (dis[v] > dis[x.id] + Edge[i].vlu)
            {
                q.push((node){v, x.vlu + Edge[i].vlu});
                dis[v] = x.vlu + Edge[i].vlu;
            }
        }
    }
    for (int i = 1; i <= n; i++)
    {
        printf("%d ", dis[i]);
    }
    return 0;
}