【二分图匹配】 双栈排序
题意
传送门
通过两个栈,4中操作,实现输入序列升序排序
- \(操作a:如果输入序列不为空,将第一个元素压入栈S_{1}\)
- \(操作b:如果栈S_{1}不为空,将S_{1}栈顶元素弹出至输出序列\)
- \(操作c:如果输入序列不为空,将第一个元素压入栈S_{2}\)
- \(操作d:如果栈S_{2}不为空,将S_{2}栈顶元素弹出至输出序列\)
如果一个\(1\sim n\)的排列\(P\)可以通过一系列操作使得输出序列为
\(1, 2,\sim,(n-1), n\),就称P是一个”可双栈排序排列”。
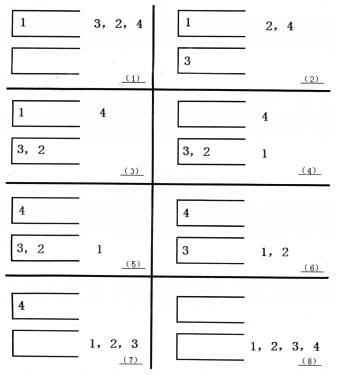
操作序列为\(<a,c,c,b,a,d,d,b>\)
另一个可行的序列为\(<a,c,c,b,a,d,d,b>\)
如果序列可双栈排序,输出字典序最小的操作
否则输出数字\(0\)
数据范围
\(1 \leq n \leq 1000\)
题解
如果只有一个栈,则整个操作顺序是固定的:
从前往后遍历每个数,每次先将当前数压入栈中,如果后面的所有数均比栈顶元素大,则将栈顶弹出,否则栈顶不能被弹出。
因此,我们只需考虑将每个数分配给哪个栈即可。
这里有个很强的性质:
两个数$ i , j ( i \leq j )$ 不能被放入同一个栈中,当且仅当存在$ k , k > j $且 \(q [k] < q [i] < q [j]\)
性质证明:
必要性:
如果有 \(i < j < k\), 且 \(q[k] < q[i] < q[j]\),则因为 \(q[i]\) 和 \(q[j]\)的后面均存在一个更小的\(q[k]\),因此\(q[i]\)和\(q[j]\)都不能从栈中被弹出,所以从栈底到栈顶的元素就不是单调的降序了,那么弹出时得到的序列就会出现逆序对。因此\(q[i]\)和\(q[j]\)不能被分到同一个栈中。
充分性:
如果\(q[i]\)和\(q[j]\)不满足上述条件,则我们在操作过程中一定不会出现矛盾。
在操作过程中,如果当前要入栈的数是\(q[j]\),那么此时:
所有大于\(q[j]\)的元素,都一定在栈中;
所有小于\(q[j]\)的元素,比如\(q[i] < q[j]\),则由于后面不存在\(q[k] < q[i]\),因此\(q[i]\)一定已经出栈;
所以此时将\(q[j]\)压入栈中后,从栈底到栈顶仍然可以保持降序,因此整个进栈、出栈过程是可以顺利进行的。
有了上述性质后,我们只需将所有满足条件的点分到两个栈中去即可。这一步可以转化成图论问题:
如果\(i, j\)满足条件,则在i和j之间连一条边。
然后判断是否是二分图即可。
答案要求字典序最小,因此从前往后染色时,需要优先将当前点分配到第一个栈中。
时间复杂度
建图时需要枚举所有点对,时间复杂度是\(O(n^{2})\)。
染色法判定二分图的时间复杂度是 \(O(n+m)\)
最后模拟栈排序的过程需要 \(O(n)\) 的计算量。
因此总时间复杂度是 \(O(n^{2})\)
Code
cpp
#include <bits/stdc++.h>
using namespace std;
const int N=1010;
int n;
int a[N];
int f[N];
int color[N];
bool g[N][N];
stack<int>stk1,stk2;
bool dfs(int u,int c){
color[u]=c;
for(int i=1;i<=n;i++){
if(g[u][i]){
if(color[i] == c)
return 0;
if(color[i] == -1 && !dfs(i,!c)) return 0;
}
}
return 1;
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>n;
memset(g,0,sizeof g);
for(int i=1;i<=n;i++)
cin>>a[i];
f[n+1]=n+1;
for(int i=n;i>=1;i--)
f[i]=min(f[i+1],a[i]);
for(int i=1;i<=n;i++)
for(int j=i+1;j<=n;j++)
if(a[i] < a[j] && f[j+1] < a[i])
g[i][j]=g[j][i]=1;
memset(color,-1,sizeof color);
for(int i=1;i<=n;i++)
if(color[i]==-1 && !dfs(i,0)){
cout<<0<<endl;
return 0;
}
int now = 1;
for(int i = 1; i<=n;i++){
if(color[i]==0) {
stk1.push(a[i]);
cout<<'a'<<' ';
}
else {
stk2.push(a[i]);
cout<<'c'<<' ';
}
while(1){
if(stk1.size() && stk1.top()==now){
cout<<'b'<<' ';
stk1.pop();
now++;
}
else if(stk2.size() && stk2.top()==now){
cout<<'d'<<' ';
stk2.pop();
now++;
}
else break;
}
}
cout<<endl;
}



