【区间选点】 Radar installation

传送门

题意

\(n\)个小岛，每个小岛都位于\(x\)轴上方，给出其坐标\((x_{i},y_{i})\)，一个雷达可以监控半径为\(r\)的区域，
雷达都位于\(x\)轴上，给出每个小岛的具体坐标以及雷达的监测范围，求出能覆盖所有小岛的最少雷达个数

数据范围

\(1\leq n\leq 1000\)

题解

如下图所示，对于任意一个小岛 \((x,y)\)，我们都可以在海岸线上求出能覆盖该小岛的建造雷达的区间 \([a,b]\)。

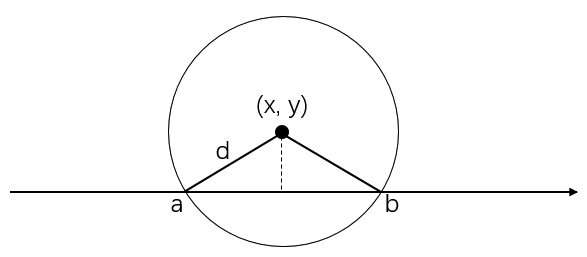
• 由勾股定理可知：
  • \(a=x-\sqrt{d^{2}-y^{2}}\)
  • \(b=x+\sqrt{d^{2}-y^{2}}\)

根据以上将所有的小岛在坐标轴上雷达能够安置的左右端点写入，将所有小岛转化成区间后，问题转化为：
给定 \(n\) 个区间，在 \(x\) 轴上选择尽量少的点，使得所有区间至少包含一个点。

• 首先将区间按照左端点从小到大排序
• 每个区间选择右端点，因为当前的右端点可能会位于后面的区间内部，并且能保证当前区间

Code

#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,n) for(int i=a;i<n;i++)
#define per(i,a,n) for(int i=n-1;i>=a;i--)
#define ll long long
#define fi first
#define se second 
typedef pair<int,int> pii;
const int N=1e5+10;
pii a[N];
int n,r;
struct Node{
    int x,y;
    double l,r;
    bool operator < (const Node &x) const {
        return l<x.l;
    }
}e[N];
int main(){
    bool ok=1;
    scanf("%d%d",&n,&r);
    rep(i,0,n) {
        scanf("%d%d",&e[i].x,&e[i].y);

        if(e[i].y > r) {
            ok=0;
            break;
        }
    }
    if(!ok){
        puts("-1");
        return 0;
    }

    rep(i,0,n){
        double k=sqrt(r*r - (double)e[i].y* e[i].y);
        e[i].l=e[i].x-k;
        e[i].r=e[i].x+k;
    }
    sort(e,e+n);
    int ans=0;
    double now=-1e9;
    rep(i,0,n){
        if(now < e[i].l){
            ans++;
            now=e[i].r;
        }
        else
            now=min(now,e[i].r);
    }
    printf("%d\n",ans);
}