manacher 原理

# Manacher

  ## 性质 

一个回文串里包含着另一个回文串，那这个回文串的另一边必然存在另一个与它一模一样的回文串

  ## 插入分隔符

奇偶造成了对称轴的位置可能在字符上，同国在原串中插入不会出现的字符如 ' # ' 

因为 n 个数 有n-1 个空隙 当n为奇数 n-1 为偶数，奇数加偶数仍然为奇数，
当 n 为偶数，n-1 奇数，奇数加偶数变为奇数，所以只需要考虑奇数情况即可
这样就可以以每个字符为对称轴进行扩展

0 1 2 3
a b c d
0 1 2 3 4 5 6 7 8 9
# # a # b # c # d #

利用一个辅助数组hw[ i ] 表示 i 点能够扩展出的回文长度，先设置一个辅助变量maxright，

表示已经达到的最右边的字符，变量mid表示包含maxright 的回文串的对称轴的位置

 

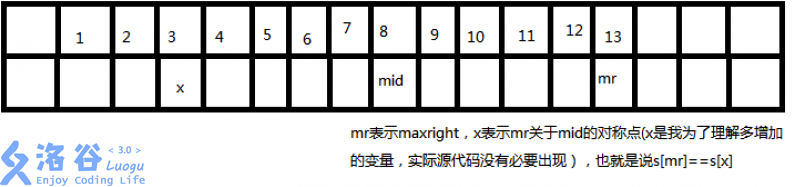
当 i 位于maxright 左边 mid 的右边的时候
设 i 关于 mid 的 对称点为 j
j 根据对称性易求得 j =mid+( mid - i )=( mid * 2 ) - I

可以将因为在当前最大回文子串内保证了整体是一个回文串，
所以左边如果存在一个回文串右边必定存在一个相等的回文串，
可以直接令hw [ i ] = hw [ j ]

如果 i 位于 maxright 右边，则按照brute 来并更新maxright 和 mid 即可

当 j-hw[ j ] < maxleft 的时候，即 i + hw[ j ] >maxright
这种情况下直接将 hw[ i ] = hw[ j ]是错误的，因为不能保证整体位于大的回文串内.

  ## 每个中心回文串子串的个数

hw/2 即以 i 为中心的回文子串的个数

  ## 每个中心回文子串的长度
hw[ i ]-1即以 i 为中心的回文串的长度