生日蛋糕 剪枝

# 题意

体积固定为 n π 、固定m层，每一层都是一个圆柱体，

从上往下，圆柱的半径、高度二者必须都是递减的，
也就是 r[i+1]>r[i] 、 h[i+1]>h[i]
找出一个方案使得整个圆柱的外表面积最小（除了最底下那一层的下低面）
最后的答案除π

# 题解

状态包含的状态有当前的层数、已经确定的体积、已经确定的面积

题目中对最后的答案除圆周率，所以可以直接忽略
剪枝：
1）优化搜索顺序 蛋糕从底向上搜索
2）上下界剪枝 当前的半径一定小于上一层，最大是上一层-1 或 sqrt（n-v）
当前的高度也一定小于上一层，最大是上一层-1 或 (n-v)/R^2
高度中有一个需要根据R求出所以先枚举R
R ∈ [ deep , min( ｜sqrt(n-v)｜, r[deep+1]-1 ) ]
H ∈[ deep , min( (n - v) / R^2 , h[deep +1) -1 ]
3）可行性剪枝 预处理从上往下前 i 层的最小体积和侧面积，1～i 层的高度和半径最小为1,2,3,……,i，如果当前的体积加上前 i 层的最小体积>n直接回溯
4）最优性剪枝
1. 若 i 层表面积加上前面已经得到的侧面积大于搜索到的答案，剪枝    

2. 1~u层的体积  =  

      1~u层的面积为  　　　　　

                        

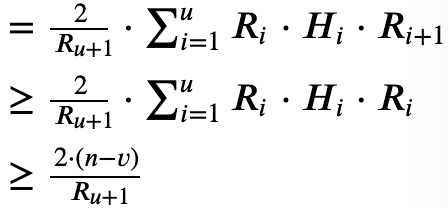
因为  可以求得，所以放缩成可以用  表示的不等式

当  大于已搜到的答案的时候，剪枝

#include<bits/stdc++.h>
using namespace std;
const int N=25;
int n,m;
int R[N],H[N];
int minv[N],mins[N];
int ans=INT_MAX;
void dfs(int u,int v,int s){
    if(v+minv[u] > n) return;
    if(s+mins[u] >= ans) return;
    if(2*(n-v)/R[u+1]+s>=ans) return;//关键最优性剪枝

    if(!u){
        if(v==n) ans=s;//剪枝将所有大的都剪掉了剩下的一定是能够更新最小值的
        return;
    }
    for(int r = min( R[u+1]-1,(int)sqrt(n-v)); r >= u; r --)//优化搜索顺序，先从大的r开始，h由r确定最大
        for(int h = min( H[u+1] - 1, (n - v) / r / r); h >= u; h--){
            int t=0;
            if(u==m)
                t=r*r;
            R[u]=r;
            H[u]=h;
            dfs(u-1,v+r*r*h,s+t+2*r*h);
        }
}
int main(){
    cin>>n>>m;

    for(int i=1;i<=m;i++){
        minv[i]=i*i*i;
        mins[i]=2*i*i;
    }
    R[m+1]=H[m+1]=INT_MAX;

    dfs(m,0,0);
    cout<<ans<<endl;
}