从一道期中题到组合

杭州某高中高一期中考试最后一道题目涉及到组合数学和数论的分拆数问题，题目如下：

前两问是平凡的，第三问官方解答如下：

上述标准解答最后的论证有点不严谨，只需要注意到

1. n为奇数的时候，偶数排列个数\(f_n=0\)，奇数排列个数\(g_n\geq 1\).
2. \(n=2,4\),有\(f_n =g_n\)
3. \(n\geq6\)且是偶数，构造一个偶数分拆到奇数分拆的映射
   \((a_1,a_2,...a_k) \overset{\phi}{\rightarrow} (1,1,...,1,a_1-1,a_2-1,...a_k-1)\)。可以发现每一个奇数分拆都有唯一的偶数分拆对应，但是反过来存在奇数分拆\(n=n-3+3\)没有偶数分拆与之对应，所以这个映射是单射，自然证明了\(f_n<g_n\)。
   综上，\(n \in N^*\) 都有\(f_n\leq g_n\)。

正整数的分拆

1.加性数论

从一般的角度考虑，整数分拆属于加性数论的问题。该领域的一般问题指的是，假设一个一列正整数\(a_1,a_2,...a_n\)构成的集合A，假设

\[n=a_{i_1},a_{i_1},...a_{i_s} \]

根据不同的问题，其中每个数a可以相同也可以不同，次序有时也可以改变，在某个和问题有关限制条件下所有可能的数列\(\{ a_{i_n}\}\)
的情况总数我们记\(r(n)\)，对于\(r(n)\)，我们会研究它是否是整数，对于一般的n是否有通项。

2.从简单例子出发

取A是\(A=(1,2,3,...)\), s无限制,
可重复，不考虑次序，称作无限划分问题。
自然数5的划分是

\[5= 4+1 =3+2=3+1+1=2+2+1=2+1+1+1\\ =1+1+1+1+1 \]

共7个。
由于不考虑次序，不妨假设数字从小到大排列，用\(p(n)\)记n的分划个数，那么\(p(5)=7\)
这里我们用\(p(n,k)\)表示n的k分拆的个数，\(p(n)\)表示n的所有分拆的个数。
其中k分拆是把n表示成k个正整数的和。

\[n=n_1+n_2+...+n_k \]

其中\(n_i>0(1\leq i \leq k)\)
有下列结论

\[(1) p(n,k)=0(k>n)\\ (2) p(n) = \sum_{k=1}^n p(n,k)\\ \]

有下列递推关系

\[p(n+k,k)=p(n,1)+p(n,2)+...+p(n,k)\\ p(n,1)=1,p(1,1)=1 \]

证明的技巧很经典，构造一个映射\(\phi\):

\[[n_1,n_2,...n_m]\overset{\phi}{\rightarrow}[(n_1+1),(n_2+1),(n_3+1),...,1,1]\ \]

这个映射把每一个n的m(\(m\leq k\))分拆映射到了n+k的k分拆。
我们证明\(\phi\)是双射，则表示像集和原像集相同，等式得证。
（双射需要注意到，不同m分拆对应不同的k分拆，每一个k分拆反过来都有m分拆和它对应）
应用
例1 计算9的5分拆个数

\[p(9,5) = p(4,1)+p(4,2)+p(4,3)+p(4,4)+p(4,5)= 1+2+1+1+0=5 \]

3.Ferrers图

数形结合来研究分拆问题，就视同内销Ferrers图的手段。
已知\(15=5+5+3+2\)，它的Ferrers图是,

如果一个Ferrers图是行和列互换，得到一个Ferrers图的共轭图，所以上图的共轭图是

对应的分拆是\(15=4+4+3+2+2\)，这也是上一个分拆的共轭分拆，如果一个分拆的共轭分拆是自身，则成为自共轭分拆。

通过这两个例子，可以得到一般情况下的Ferrers图的画法

\[n=n_1+n_2+...+n_k(n_1\geq n_2\geq ...\geq n_k) \]

则第\(i\)行我们画\(n_i\)个点,并且上下行对齐。

有以下定理

定理3.1：n的k分拆（就是n拆开为k个数的和）的个数等于n的最大分量是k的分拆数

定理3.2：n的自共轭分拆个数等于n的各个分量是奇数且两两不等的分拆的个数

定理3.3：n的分拆分量两两不相等的分拆的个数等于n的各个分量是奇数的分拆的个数

用Ferrers图 数形结合可以证明。

3.1分配问题

分配问题指的是，n个球放在r个盒子里，有多少种不同类型的分配方案数。
主要考虑三个方面

1.n个球完全相同还是完全不同
2.是否允许有空盒子
3.n个盒子完全相同还是完全不同

有各种情况的分配方案数。

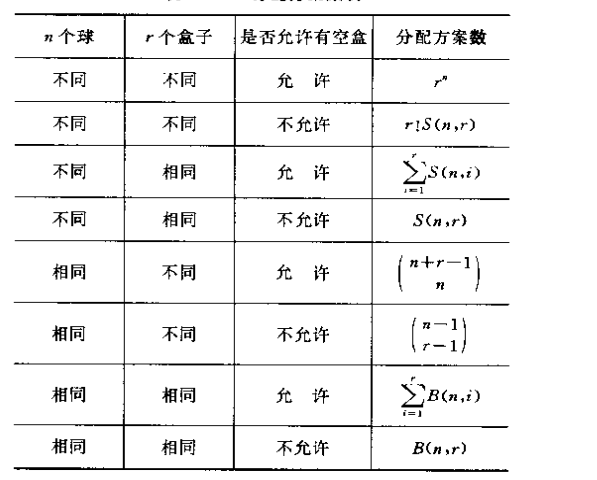
其中\(S(n,k)\)是第二类Stirling数。表示将n个不同的数，划分成为k个互不区分的非空子集的方案数。

相关介绍如下（其中花括号是\(S(n,k)\)）：
递推式

\[S(n,k)=S(n - 1,k - 1)+kS(n - 1,k) \]

边界是\(S(n,0)=0,S(0,0)=1,S(n,1)=1\)
考虑用组合意义来证明。我们插入一个新元素时，有两种方案：

1. 将新元素单独放入一个子集，有\(S(n - 1,k - 1)\)种方案；
2. 将新元素放入一个现有的非空子集，有\(kS(n - 1,k)\)种方案。

第二类斯特林数\(S(n,m)\)的通项公式为：\(S(n,m)=\sum_{i = 0}^{m}\frac{(-1)^{m - i}i^{n}}{i!(m - i)!}\)。

例\(：(x + y + z)^4\)的展开式有多少项？

解：\((x + y + z)^4\)的展开式中的每一项都是 4 次方，相当于将 4 个无区别的球放入 3 个有标志的盒子 x，y，z 里，每个盒子中放进的球不加限制。

例如，\(x^4\)相当于将 4 个球都放进盒子 x 中，盒子 y，z 为空；\(x^2yz\)相当于将 2 个球放进盒子 x 中，盒子 y，z 中各放进一个球。所以，\(r = 4\)，\(n = 3\)，项数

\[N=\binom{4 + 3 - 1}{4}=\binom{6}{4}=15 \]

这 15 项分别为
\(x^{4},x^{3}y,x^{3}z,x^{2}yz,x^{2}y^{2},x^{2}z^{2},xy^{3},xz^{3},xyz^{2},xy^{2}z,y^{2}z^{2},y^{3}z,z^{3}y,y^{4},z^{4}\)

生成函数

生成函数主要想法是对于一个有限或者无限的数列

\[\{ a_0,a_1,a_2,... \} \]

和一个幂级数联系，这个幂级数就是这个数列的生成函数。

\[A(x) = a_0 +a_1 x+ a_2 x^2+... \]

有了函数，我们就可以发挥微积分的力量，从而将组合问题解析化。这种将不同数学领域联系起来的工具是很有力量的。
例：由恒等式\((1 + x)^{m + n}=(1 + x)^{m}(1 + x)^{n}\)
可以推导出 Vandermonde 恒等式

\[\binom{m + n}{r}=\sum_{k = 0}^{n}\binom{m}{k}\binom{n}{r - k} \]

只需要注意到等式两端\(x^r\)的系数相等。

下面列出几个常见的简单数列的生成函数：

1. \(G\{1\}=\frac{1}{1 - x}\)；
2. \(G\{a^{k}\}=\frac{1}{1 - ax}\)；
3. \(G\{k\}=\frac{x}{(1 - x)^{2}}\)；
4. \(G\{k(k + 1)\}=\frac{2x}{(1 - x)^{3}}\)；
5. \(G\{k^{2}\}=\frac{x(1 + x)}{(1 - x)^{3}}\)；
6. \(G\{k(k + 1)(k + 2)\}=\frac{6x}{(1 - x)^{4}}\)；
7. \(G\{\frac{1}{k!}\}=e^{x}\)；
8. \(G\{\binom{\alpha}{k}\}=(1 + x)^{\alpha}\)；
9. \(G\{\binom{n + k}{k}\}=\frac{1}{(1 - x)^{n + 1}}\)。

4.分拆数的生成函数

定理4.1：令\(B(n)\)表示正整数\(n\)的所有分拆数，\(B_r(n)\)表示\(n\)的各分部量都不超过\(r\)的分拆数，\(B_H(n)\)表示\(n\)的各分部量都属于集合\(H\)的分拆数，则它们相应的生成函数分别为：

1. 正整数\(n\)的各分部量都不超过\(r\)的分拆数\(B_r(n)\)相应的生成函数为：\(\sum_{n=0}^{\infty} B_{r}(n) x^{n}=\frac{1}{(1 - x)(1 - x^{2})\cdots(1 - x^{r})}\)；
2. 正整数\(n\)的各分部量都属于集合\(H\)的分拆数\(B_H(n)\)相应的生成函数为：\(\sum_{n=0}^{\infty} B_{H}(n) x^{n}=\prod_{j \in H} \frac{1}{1 - x^{j}}\)；
3. 正整数\(n\)的所有分拆数\(B(n)\)相应的生成函数为：\(\sum_{n=0}^{\infty} B(n) x^{n}=\prod_{j = 1}^{\infty} \frac{1}{1 - x^{j}}\)。

推论1：将\(n\)分成\(r\)个分部量的分拆数的生成函数为

\[\frac{x^{r}}{(1 - x)(1 - x^{2})\cdots(1 - x^{r})} \]

推论2 :n的各个分部两两不同的分拆数等于n的各部分量都是奇数的分拆数。

5.Euler的两个公式

定理5.1：\((1 + x)(1 + x^{3})(1 + x^{5})\cdots = 1+\frac{x}{1 - x^{2}}+\frac{x^{4}}{(1 - x^{2})(1 - x^{4})}+\frac{x^{9}}{(1 - x^{2})(1 - x^{4})(1 - x^{6})}+\cdots\)

定理5.2：\((1 + x^{2})(1 + x^{4})(1 + x^{6})\cdots = 1+\frac{x^{2}}{1 - x^{2}}+\frac{x^{6}}{(1 - x^{2})(1 - x^{4})}+\frac{x^{12}}{(1 - x^{2})(1 - x^{4})(1 - x^{6})}+\cdots\)

欧拉的证明巧妙而且初等
只需要证明

\[(1 + ax)(1 + ax^{3})(1 + ax^{5})\cdots = 1+\frac{ax}{1 - x^{2}}+\frac{a^{2}x^{4}}{(1 - x^{2})(1 - x^{4})}+\cdots \]

设一个函数

\[K(a) = K(a,x) = (1 + ax)(1 + ax^{3})(1 + ax^{5})\cdots = 1 + c_1 a + c_2 a^2 + \cdots\\ 显然有\\ K(a) = (1+ax) K(ax^2) \]

也就是

\[ 1 + c_1 a + c_2 a^2 + \cdots = (1+ax)( 1 + c_1 a x^2+ c_2 a^2 x^4 + \cdots) \]

根据对应系数相等有

\[c_1 = x +c_1 x^2 \\ c_2 =c_1 x^3 +c_2 x^4 \cdots \\ c_m = c_{m-1} x^{2m-1} + c_m x^{2m} \]

\(c_m=\frac{x^{2m - 1}}{1 - x^{2m}}c_{m - 1}\)，进一步推导可得

\[c_m=\frac{x^{1 + 3 +\cdots+(2m - 1)}}{(1 - x^{2})(1 - x^{4})\cdots(1 - x^{2m})}=\frac{x^{m^{2}}}{(1 - x^{2})(1 - x^{4})\cdots(1 - x^{2m})} \]

\(a=1和a=x\)上述结论得证。

顺着上面两个定理的思路.

设

\[K_{j}(a)=K_{j}(a,x)=(1 + ax)(1 + ax^{2})\cdots(1 + ax^{j})=\sum_{m = 0}^{j}c_{m}a^{m} \]

那么\((1 + ax^{j + 1})K_{j}(a)=(1 + ax)K_{j}(ax)\)。

将幂级数代入，并令\(a^{m}\)的系数相等，就得到

\[c_{m}+c_{m - 1}x^{j + 1}=(c_{m}+c_{m - 1})x^{m} \]

也就是对\(1\leq m\leq j\)有

\[(1 - x^{m})c_{m}=(x^{m}-x^{j + 1})c_{m - 1}=x^{m}(1 - x^{j - m + 1})c_{m - 1} \]

从而有：

\[(1 + ax)(1 + ax^{2})\cdots(1 + ax^{j})=1 + ax\frac{1 - x^{j}}{1 - x}+a^{2}x^{3}\frac{(1 - x^{j})(1 - x^{j - 1})}{(1 - x)(1 - x^{2})}+\cdots + a^{m}x^{\frac{1}{2}m(m + 1)}\frac{(1 - x^{j})\cdots(1 - x^{j - m + 1})}{(1 - x)\cdots(1 - x^{m})}+\cdots+a^{j}x^{\frac{1}{2}j(j + 1)} \]

还有以下定理
公式

\[\begin{aligned}\frac{1}{(1 - ax)(1 - ax^{2})\cdots(1 - ax^{j})}=&1 + ax\frac{1 - x^{j}}{1 - x}+a^{2}x^{2}\frac{(1 - x^{j})(1 - x^{j + 1})}{(1 - x)(1 - x^{2})}\\&+\cdots.\end{aligned} \]

特别地，如果取\(a = 1\)，并令\(j\to\infty\)，就得到：
公式

\[\frac{1}{(1 - x)(1 - x^{2})\cdots}=1+\frac{x}{1 - x}+\frac{x^{2}}{(1 - x)(1 - x^{2})}+\cdots \]

6.Jacobi恒等式

此公式在椭圆函数论中会出现。

定理6.1 ：如果\(\vert x\vert\lt1\)，那么，对除了\(z = 0\)以外所有的\(z\)都有：

\[\prod_{n = 1}^{\infty}\left\{\left(1 - x^{2n}\right)\left(1 + x^{2n - 1}z\right)\left(1 + x^{2n - 1}z^{-1}\right)\right\}=1+\sum_{n = 1}^{\infty}x^{n^{2}}\left(z^{n}+z^{-n}\right)=\sum_{-\infty}^{\infty}x^{n^{2}}z^{n}. \]

如果在Jacobi恒等式的左边用\(x^{k}\)代替\(x\)，用\(-x\)和\(x\)代替\(z\)，并用\(n + 1\)代替\(n\)，就得到：

\[\prod_{n = 0}^{\infty}\left\{\left(1 - x^{2kn + k - 1}\right)\left(1 - x^{2kn + k + i}\right)\left(1 - x^{2kn + 2k}\right)\right\}=\sum_{n = -\infty}^{\infty}(-1)^{n}x^{kn^{2}+in} \]

\[\prod_{n = 0}^{\infty}\left\{\left(1 + x^{2kn + k - 1}\right)\left(1 + x^{2kn + k + l}\right)\left(1 - x^{2kn + 2k}\right)\right\}=\sum_{n = -\infty}^{\infty}x^{kn^{2}+ln}.\quad \]

某些特殊情形是特别有趣的。

1. \(k = 1\)，\(l = 0\)给出：

   • \(\prod_{n = 0}^{\infty}\left\{\left(1 - x^{2n + 1}\right)^{2}\left(1 - x^{2n + 2}\right)\right\}=\sum_{n = -\infty}^{\infty}(-1)^{n}x^{n^{2}}\)
   • \(\prod_{n = 0}^{\infty}\left\{\left(1 + x^{2n + 1}\right)^{2}\left(1 - x^{2n + 2}\right)\right\}=\sum_{n = -\infty}^{\infty}x^{n^{2}}\)，这是两个来自椭圆函数论的标准公式。

2. 在上述公式中取\(k = l = 2\)则得：

   • \(\prod_{n = 0}^{\infty}\left\{\left(1 - x^{3n + 1}\right)\left(1 - x^{3n + 2}\right)\left(1 - x^{3n + 3}\right)\right\}=\sum_{n = -\infty}^{\infty}(-1)^{n}x^{\frac{1}{2}n(3n + 1)}\)
     这也就是：

定理6.2：

\[(1 - x)\left(1 - x^{2}\right)\left(1 - x^{3}\right)\cdots=\sum_{n = -\infty}^{\infty}(-1)^{n}x^{\frac{1}{2}n(3n + 1)} \]

这个著名的 Euler 恒等式也可以写成形式：

\[(1 - x)\left(1 - x^{2}\right)\left(1 - x^{3}\right)\cdots = 1+\sum_{n = 1}^{\infty}(-1)^{n}\left\{x^{\frac{1}{2}n(3n - 1)}+x^{\frac{1}{2}n(3n + 1)}\right\}=1 - x - x^{2}+x^{5}+x^{7}-x^{12}-x^{15}+\cdots. \]

定理6.3

\[\frac{(1 - x^{2})(1 - x^{4})(1 - x^{6})\cdots}{(1 - x)(1 - x^{3})(1 - x^{5})\cdots}=1 + x + x^{3}+x^{6}+x^{10}+\cdots. \]

其中右边的指数是三角数(形如\(\frac{1}{2} n (n+1)\))。

(取\(k = 5/2\)，\(l = 3/2\)及\(k = 5\)，\(l = 1/2\)则得：

定理6.4

\[\prod_{n = 0}^{\infty}\left\{\left(1 - x^{5n + 1}\right)\left(1 - x^{5n + 4}\right)\left(1 - x^{5n + 5}\right)\right\}=\sum_{n = -\infty}^{\infty}(-1)^{n}x^{\frac{1}{2}n(5n + 3)} \]

定理6.5：

\[\prod_{n = 0}^{\infty}\left\{\left(1 - x^{5n + 2}\right)\left(1 - x^{5n + 3}\right)\left(1 - x^{5n + 5}\right)\right\}=\sum_{n = -\infty}^{\infty}(-1)^{n}x^{\frac{1}{2}n(5n + 1)} \]

7.分拆数的渐近估计

当\(n\to+\infty\)时，\(p(n)\to+\infty\)。Macmahon 算出了\(p(200)=3972999029388\)。

定理7.1（Hardy-Ramanujan）：\(p(n)\sim\frac{c^{-\sqrt{n}}}{\sqrt{4\times3n}}\)。

Ramanujan 通过研究 Macmahon 作的\(p(n)\)的表，还发现了下面的同余式：

定理7.2（Ramanujan）

• \(p(5n + 4)\equiv 0\pmod{5}\)；
• \(p(7n + 5)\equiv 0\pmod{7}\)；
• \(p(11n + 6)\equiv 0\pmod{11}\)。

第一条可记为\(\sum_{n=0}^{\infty}p(5n + 4)=5\times\cdots\)。

Ramanujan 提出了一般的猜想：如果\(\delta = 5^{a}7^{b}11^{c}\)，且\(24n\equiv1\pmod{\delta}\)，则\(p(n)\equiv0\pmod{\delta}\)。只需要研究\(\delta = 5^{a}\)，\(7^{b}\)，\(11^{c}\)的情形，所有其他情形都可以作为推论从这些情形推出。

定理7.3：(Rogers-Ramanujan 公式)

• \(\prod_{n = 0}^{\infty}\frac{1}{(1 - x^{5n + 1})(1 - x^{5n + 4})}=1+\sum_{n = 1}^{\infty}\frac{x^{n^{2}}}{(1 - x)(1 - x^{2})\cdots(1 - x^{n})}\)；
• \(\prod_{n = 0}^{\infty}\frac{1}{(1 - x^{5n + 2})(1 - x^{5n + 3})}=1+\sum_{n = 1}^{\infty}\frac{x^{n(n + 1)}}{(1 - x)(1 - x^{2})\cdots(1 - x^{n})}\)

8.编程实现

通过用python编写程序计算，输入整数n，输出所有n的分拆的可能，代码如下：
编程思路 从小到大对n分拆

def split_number(n, seq):
    #print(n, seq)
    if sum(seq) == n:
        print(seq)
        return
    for i in range(1, n):
        if len(seq) == 0:
            tmp = []
            tmp.append(i)
        elif i >= seq[-1] and sum(seq) + i <= n:
            tmp = seq[:]
            tmp.append(i)
        else:
            continue
        split_number(n, tmp)

split_number(7, [])

输出结果表示7的分拆情况（共15种）：

[1, 1, 1, 1, 1, 1, 1][1, 1, 1, 1, 1, 2][1, 1, 1, 1, 3] [1, 1, 1, 2, 2] [1, 1, 1, 4][1, 1, 2, 3][1, 1, 5][1, 2, 2, 2][1, 2, 4][1, 3, 3][1, 6][2, 2, 3][2, 5][3, 4][7]