树、二叉树、查找算法总结

思维导图

笔记

一、基本概念：

1、列表：待搜索的数据集合。
2、关键字：要查找的那个数据。
3、查找，检索：一种算法过程。给出一个key值（关键字），在含有若干个结点的序列中找出它。
4、查找表：同一类型的数据元素的集合。
5、静态查找表：查询某个元素、检索指定元素的属性。
6、动态查找表：查找后插入、删除。
7、查找成功：当某个元素的key值等于给定值k，返回该元素的位置。
8、查找失败：所有元素的key值均不等于给定的值k，返回表示失败的标识。

二、基于线性表的查找：

1、顺序查找：<适合对象——无序或有序队列>

(1)思想：逐个比较，直到找到或者查找失败。
(2)时间复杂度：T(n) = O(n)。
(3)空间复杂度：S(n) = O(n)。
(4)缺点：当n较大时，平均查找长度较大，效率低。

2、折半查找：<适合对象——只是适用于有序表，且限于顺序存储结构(线性链表无法进行折半查找)>

1)思想：又称二分查找，对于已经按照一定顺序排列好的列表，每次都用关键字和中间的元素对比，然后判断是在前部分还是后部分还是就是中间的元素，然后继续用关键字和中间的元素对比。
(2)时间复杂度：T(n) =O(logn)。具有n 个结点的完全二叉树的深度为，在这里尽管折半查找判定二叉树并不是完全二叉树，但同样相同的推导可以得出，最坏情况是查找到关键字或查找失败的次数也如此。其时间复杂度远好于顺序查找的时间复杂度O(n)了。

3、分块查找：<适合对象——块内的元素可以无序，但块之间是有序的>

(1)思想：把无序的列表分成若干子块（子表），然后建立一个索引表，记录每个子块中的某个关键字（最大的数或是最小的数），然后用关键字和这个索引表进行对比。该索引表还存储子块的起始位置，所以可以使用折半查找或者顺序查找确定关键字所在的子块位置。进入子块后，使用顺序查找查找。
(2)结构：分块索引的索引项结构分三个数据项，最大关键码，它存储每一块中的最大关键字，这样的好处就是可以使得在它之后的下一块中的最小关键字也能比这一块最大的关键字要大；块长，便于循环时使用；首数据元素指针，便于开始对这一块中记录进行遍历。
(3)时间复杂度：O(logn)

三、基于树的查找：

1、二叉排序树：

1)思想：二叉排序树：①若它的左子树非空，则左子树上所有节点的值均小于它的根节点的值；②若它的右子树非空，则右子树上所有结点的值均大于（或大于等于）它的根节点的值；③它的左、右子树也分别为二叉排序树。查找的时候，中序遍历二叉树，得到一个递增有序序列。查找思路类似于折半查找。
(2)时间复杂度：插入一个节点算法的O(㏒n)，插入n个的总复杂度为O(n㏒n)。

四、计算式查找：

1、哈希查找：

(1)思想：首先在元素的关键字k和元素的存储位置p之间建立一个对应关系H，使得p=H(k)，H称为哈希函数。创建哈希表时，把关键字为k的元素直接存入地址为H(k)的单元；以后当查找关键字为k的元素时，再利用哈希函数计算出该元素的存储位置p=H(k)，从而达到按关键字直接存取元素的目的。难点在于处理冲突的方式：①开放定址法②再哈希法③链地址法④建立公共溢出区。
(2)时间复杂度：O(1)

五、一般树与二叉树的区别：

(1)树的结点个数至少为1，而二叉树的结点个数可以为0；
(2)树的结点最大度数没有限制，而二叉树结点的最大度数为2；
(3)树的结点无左、右之分，而二叉树的结点有左、右之分。

六、二叉树：

(1)在二叉树的第K层上，最多有 2^(k-1)(K >= 1）个结点
(2)深度为K的二叉树，最多有 2^k-1 个结点（K>=1）
(3)对于任何一棵二叉树，如果其叶子结点的个数为K，度为2的结点数为M,则K=M+1

七、满二叉树：

(1)一棵深度为k，且有2k - 1个节点的树是满二叉树。
(2)如果一颗树深度为h，最大层数为k，且深度与最大层数相同，即k=h;
(3)它的叶子数是：2(h-1)
(4)第k层的结点数是：2(k-1)
(5)总结点数是：2k - 1
(6)树高：h=log2(n+1)

八、完全二叉树：

(1)完全二叉树是由满二叉树而引出来的。对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。
(2)若设二叉树的深度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第h 层所有的结点都连续集中在最左边，这就是完全二叉树。
(3)满二叉树一定是完全二叉树，完全二叉树不一定是满二叉树。
(4)深度为k的完全二叉树，至少有2(k-1)个节点，至多有2k-1个节点。
(5)树高h=log2n + 1。

九、二叉排序树：

(1)二叉排序树又叫二叉查找树或者二叉搜索树，它首先是一个二叉树，而且必须满足下面的条件：
(2)若左子树不空，则左子树上所有结点的值均小于它的根节点的值
(3)若右子树不空，则右子树上所有结点的值均大于它的根结点的值
(4)左、右子树也分别为二叉排序树
(5)没有键值相等的节点

十、二叉树的遍历：

先序遍历

(1)访问根结点
(2)访问左子树的左子树，再访问左子树中的右子树
(3)访问右子树的左子树，再访问右子树中的右子树
(4)任意子树输出顺序为：父结点——左子结点——右子结点

中序遍历

(1)先访问左子树中的左子树，再访问左子树中的右子树
(2)访问根结点。
(3)后访问右子树中的左子树，再访问右子树中的右子树
(4)任意子树输出顺序为：左子结点——父结点——右子结点

后序遍历

(1)先访问左子树中的左子树，再访问左子树中的右子树
(2)再访问右子树中的左子树，再访问右子树中的右子树
(3)访问根结点
(4)任意子树输出顺序为：左子结点——右子结点——父结点

层次遍历

(1)访问根结点，即第1层，设为 i 层
(2)访问i+1层的结点，从左到右顺序访问
(3)层次遍历输出顺序为：根结点—— i 层结点从左到右—— i +1层结点从左到右

疑难问题及解决方案

运用前序和中序序列重建二叉树

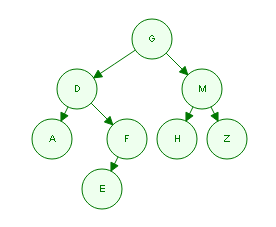
上面这个二叉树对应的3种遍历序列如下：
先序遍历: GDAFEMHZ
中序遍历: ADEFGHMZ
后序遍历: AEFDHZMG
1，因为前序遍历的第一个节点一定是一个二叉树的根，所以从前序的第一个数据开始也就是G，把G映射到中序序列中，并记下在中序序列中的位置，又因为在中序序列中是按照leftChild—root—rightChild的方式遍历的所以在中序中以上面记下的位置为分界，得到以G为根的左右子树（分别是ADEF和HMZ）。
2，上面第一步只是把整个二叉树分出左右子树，然后再在前序中找到下一个数据也就是D，再把D在中序中对应的位置记录下来，此时，D的位置并不在中序序列的最左端（最左端是A），也就说明D还可以继续向下‘派生’左子树，那么继续访问前序序列中的下一个元素也就是A。
3，同样的步骤，A在中序序列中的位置处于最左端（即A的左子树长度为0），这说明A不能够再有左子树，此时便可以把A的左子树置为null，这时候再考虑A的右子树是否存在，因为在中序序列中A的右面是D，但是D是A的父节点，所以A的右子树置为null。
4，类似的方式再考虑D的右子树存在问题，如果右子树长度不是0，那么就在前序中选出相应的数据。

7-3 jmu-ds-二叉树叶子结点带权路径长度和 (25分)

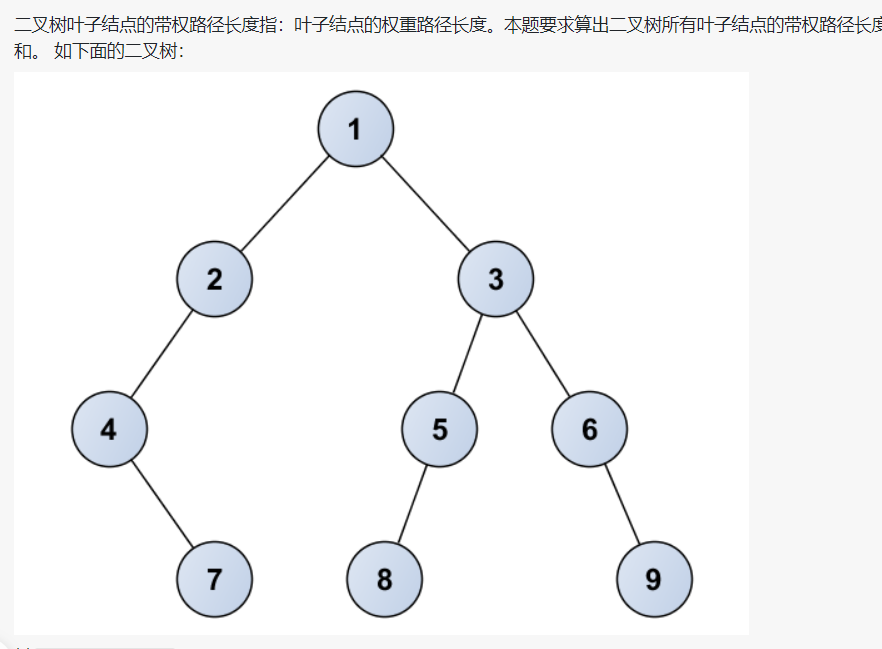
未解决。。